13.Вычисление двойного интеграла в декартовых и полярных координатах.

В декартовых:Пусть область D - правильная в отношении оси Ох (рис. 2.6.)

Тогда в этом случае область D может быть задана одной системой неравенств:

Если существует двойной интеграл 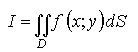(это возможно, например, если f(x; y) непрерывна на D), то его можно вычислить через повторный кратный интеграл так: При этом внутренний интеграл по у находится при постоянном х.

Данное представление (2.11) получается из определения двойного интеграла при специальном способе разбиения области D на n "мелких" частей (линиями, параллельными либо Ох, либо Оу - прямоугольной "шахматной" сеткой. А затем выполняется суммирование "объёмов" ΔV_i сначала по оси Оу, а затем по оси Ох).

В полярных

П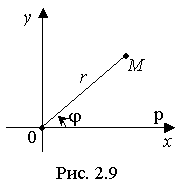 усть на плоскости Оху одновременно введена и полярная система координат Orφ (рис. 2.9): Оp  — полярная ось, которая совпадает с осью Ох; φ    — полярный угол; r     — полярный радиус точки М. Тогда, как известно:

Для полярной системы координатная сетка представляет собой пересечение окружностей увеличивающихся радиусов r с лучами, выходящими из точки О под возрастающими углами φ к полярной оси (рис. 2.10).

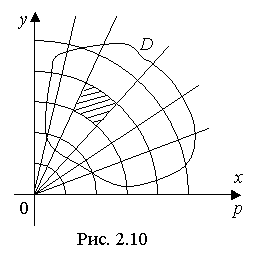
Рассмотрим элементарный участок полярной сетки (рис. 2.11). Тогда его площадь ΔS можно найти как разность площадей S₁ и S₂ полярных секторов радиусов r + Δr и r с раствором угла Δφ:

При Δr → 0, Δφ → 0 получаем ΔS ≈ r · Δr · Δφ. Таким образом, при замене переменных по формуле (2.12) дифференциал площади в полярной системе координат преобразуется так:

Напомним, что в декартовой системе координат Оху прямоугольная сетка дает dS = dx · dy.)

Замечание.

Формулу (2.13) можно получить и по-другому, используя Якобиан J - "коэффициент искажения" площади при переходе к другой системе координат. А именно

Что совпадает с (2.13).

Теорема 2.4.

Если область D - является правильной в полярной системе координат Оrφ, то двойной интеграл в этих координатах вычисляется так:

14.Геометрическое приложение двойного интеграла.

1)Вычисление объема.

Двойной интеграл равен объему криволинейного цилиндра, ограниченного сверху поверхностью z=f(x;y)>=0,снизу плоскостью XOY, а также боковой цилиндрической поверхностью с образующей параллельной оси OZ и направляющей в виде контура области интегрирования Р.

V=SS f(x;y)dxdy;

2)Вычисление площади плоской фигуры.

По геометрическому свойству SS 1 dxdy=площади(S),если f(x;y)=1 площадь области интегрирования Р может быть вычислена двойным интегралом.

3)Вычисление площади поверхности.

Пусть поверхность задана уравнением z=f(x;y), причем проекцией поверхности на XOY является область Р, в которой функция z=f(x;y) непрерывна вместе со своими частными производными 1-ого порядка, тогда S вычисляется по формуле

S=двойной интеграл от (1+(f_x’(x;y))²+(f_y’(x;y))²)^1/2dxdy

15.Комплексные числа. Алгебраическая, тригонометрическая и показательные формы записи. Действия над комплексными числами.

Компл. числом z=x+y наз-ся число,где x,y-действ. числа,i-мнимая единица.

x-действит. часть к.числа,у-мнимая часть. у=0

Сложение

Деление

Геометр. представление к.чисел.

К. число можно изобразить на плоскости точкой m,имеющей координаты M(x;y) на пл.хоу.Таким обр. т. М-геометр. образ компл.ч.,при этом действит. часть х к.ч. z откл-ся по оси ох;поэтому ось ох наз-ся действит.А мнимая часть у откл. по оси оу-мнимая ось.

К.ч. можно отождествить с вектором МО.Такое описание встречается в электротехнике.Модулем к.ч. z наз-ся неотр. действит. число,равное длине вектора ОМ.

Аргументом к.ч. z≠0 наз-ся величина угла φ между положит. направлением оси ох и ОМ.Отсчет угла ведется против час.стрелки.Соотношение между модулем к.ч. и его дейст. и мнимой частью у:

x=rcos φ

y=rsin φ

r=

Если в к.ч. подставить вместо х и у предыд. выр-я,то получим тригон.форму записи.

Извлечение корня:

Возведение в степень:

Формула Муавра:

.

16.Дифференциальные Ур-я

Это Ур-е связывающее переменную х, искомую ф-ю у(х) и ее производные. Если искомая ф-я есть ф-я одной переменной, то диф уравнение называется обыкновенным. Общим решением Ур-я 1 порядка наз. Ф-я у=фи(х, с), которая удовлетворяет данному уравнению. Если общее реш не вып=ражено явно, оно называется общим интегралом

Если общее решение ур-я не выражено явно,то оно наз-ся общим интегралом.

Частным решением наз-ся любая ф-ция y=j(x,co),кот. получается из общего решения y=j(x,c),если в последнем выражении произвольному пост. с присвоить определенное значение j=j(x;c),c=co.

17.Дифуры первого порядка. Методы решения.

Дифуры 1 порядка:с разделенными переменными,с разделяющимися,линейные,Бернулли,однородные.

Методы: F(x;y;y’)=0;y’=f(x;y).Т:сущ-е ед-ти р-я.Если в ур-и y’=f(x;y)ф –я f(x;y)и ее част. Пр-я f’(y)(x;y)-непр-на в неот-ой обл-ти D на пл-ти XOY сод-ей некот-ю точку D€(x0;y0), то сущ-ет един-е реш-е этого ур-я y=ф(x),удов-ет условию y(x0)=y0;Геом.смысл Т:сущ-ет и при том ед-я ф –я y=ф(x) график кот-ой пр-т через точку D€(x0;y0) и ус-е y(x0)=y0-нач-е ус-е, а зад. -наз-ся зад-ей Коши.

Методы р-я:1)ур-е с разд. Пер-ми- ур-е вида:M(x)dx+N(y)dy=0;y’=f1(x)*f2(x); M1(x)*M2(y)dx+N1(y)N29x)dy=0;метод р-я : разд. Пер-е.2)Лин-е диф. Ур-е 1 пор-ка оно линейно отн. y и y’;y’+p(x)y=f(x)метод р-я-метод под-ки.Будем искать ф-ю y как пр-е 2 ф-й;y=U(x)*V(x);3)Ур-е Бернулли:Общий вид:y’+p(x)y=f(x) ;(n≠0;1);метод р-я=(z= с пом-ю некот –ой подстановки ур- е Бернулли можно прив-ти к лин-му ур-ю.4)однор-е ур-е:y'=f(x;y) наз-ся однор. Если ф-я есть однор-я ф-я нулевого из-я т.к. для однор-го ур-я спр-во рав-во f(x;y)=f( ур-е примет вид y’=f( ;метод р-я:метод под-ки:y’=f(y/x);(y/x)=t(x);y=t(x)x;y’=t’x+t;