
- •7.1. Несобственные интегралы второго рода.
- •7.2. Несобственные интегралы первого рода.
- •13.Вычисление двойного интеграла в декартовых и полярных координатах.
- •Что совпадает с (2.13).
- •18.Дифы высших порядков. Понятия общего и частного решения.
- •23.Числовые ряды. Свойства сходящихся рядов.
- •25.Достаточные признаки сходимости рядов.
1.Неопределенный интеграл, его свойства, таблица первообразных основных функций.
Если F(х) есть первообразная
для функции f(х), то полное
семейство первообразных F(х)
+ С называется неопределенным интегралом
от функции f(х) и обозначается
![]() .
.
Свойства интегралов:
1)производная от неопределенного интеграла есть подинтегральная функция
2)Дифференциал от неопр. Интеграла равен подинтегральному выражению
3)Интеграл от дифференциала некоторой функции равен самой этой функции с точностью до постоянного слагаемого
4)Постоянный множитель можно выносить за знак интеграла
5)Интеграл от алгебраической суммы ф-ии равен алгебраической сумме ф-ии интеграла этих ф-й
6)всякая формула интегрирования сохраняет свой вид не зависимо от того является переменная интегрирования независимой Х или любой диф-ей ф-ей от Х.
Таблица.
1.
![]()
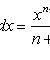
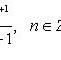
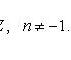
2.
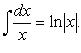
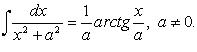
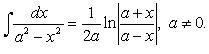
![]()
![]()
2.Основные методы интегрирования.
1) Непосредственное интегрирование – с помощью таблицы интегралов и свойств интегралов.
![]() =
=![]() =
=![]() )dx=
)dx=![]() -3
-3![]() +3lnx-x+C
+3lnx-x+C
II Метод замены переменной или метод подстановки.
а)![]() *
*![]()
1)Введём новую переменную
![]()
2)Найдём дифференциал от левой и правой частей.
![]()
3)
![]()
4)Если интеграл
=F(t)+C, то исходный интеграл
*
=![]()
III Интегрирование по «частям». Пусть U и V -дифференцируемые фцнкции
(UV)’=U’V+UV’
![]()
![]()
dy=y’dx, u’dx=du,
v’dx=dv, uv=
![]()
![]()
Типичные интегралы, которые берутся по частям:
![]()
![]()
![]()
![]() n принадлежит N
n принадлежит N
![]() ,
dv=
,
dv=
![]() ,
sinx dx,
cosx dx.
,
sinx dx,
cosx dx.
![]()
![]()
![]()
![]()
![]()
![]()
U={lnx,arcsinx, arccosx, arctgx, arcctgx,![]() }
}
![]()
Возвратные интегралы:
![]()
![]()
Интегрируя дважды по частям – выбор u и v первый раз произвольный, а второй раз выбор будет аналогичен первоначальному.
3. Интегрирование рациональных функций.
Пусть P(x) и
Q(x) –
многочлены, тогда
![]() называется рациональной функцией. Такая
дробь называется правильной, когда
степень многочлена P(x)
меньше степени многочлена Q(x).
Во всех остальных случаях дробь
неправильная.
называется рациональной функцией. Такая
дробь называется правильной, когда
степень многочлена P(x)
меньше степени многочлена Q(x).
Во всех остальных случаях дробь
неправильная.
![]()
![]() Простейшие
дроби:
Простейшие
дроби:
I![]() ,
,
A,a- действительные числа. Корень знаменателя- действительный и некратный.
II![]() Корень
знаменателя- действительный и кратный.
Корень
знаменателя- действительный и кратный.
III![]() Корни знаменателя- комплексные, но
некратные.
Корни знаменателя- комплексные, но
некратные.
IV![]() Корни знаменателя комплексные, но
кратные.
Корни знаменателя комплексные, но
кратные.
Интегрирование этих дробей.
I![]()
![]()
II![]()
![]()
![]()
III В знаменателе в квадратном
трёхчлене выделим полный квадрат, затем введём новую переменную и разобьём интеграл на два.
IV
![]() Решается с помощью рекурентных формул.
P(x)/Q(x),
где Q(x)-
многочлен степени n, то
Q(x) можно
разложить на множители.
Решается с помощью рекурентных формул.
P(x)/Q(x),
где Q(x)-
многочлен степени n, то
Q(x) можно
разложить на множители.
![]()
![]()
![]() То дробь тоже раскладывается на простейшие
дроби первого- четвёртого типов.
То дробь тоже раскладывается на простейшие
дроби первого- четвёртого типов.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() это
неизвестные коэффициенты, их необходимо
найти.
это
неизвестные коэффициенты, их необходимо
найти.
4.Интегрирование иррациональных функций.
Интегрирование иррациональных функций - Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен.
Интегралы
вида
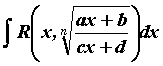 ,
где
,
где
![]() -
рациональная функция своих аргументов,
вычисляются заменой
-
рациональная функция своих аргументов,
вычисляются заменой
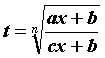 .
.
Интегралы
вида
![]() вычисляются
заменой
вычисляются
заменой
![]() или
или![]() .
.
Интегралы
вида
![]() вычисляются
заменой
вычисляются
заменой
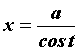 или
или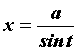 . Интегралы вида
. Интегралы вида
![]() вычисляются
заменой
вычисляются
заменой
![]() или
или![]() .
.
5.Интегрирование ф-ии, рационально зависящей от тригонометрических функций.
Интегралы
вида
![]() ,
где
-
рациональная функция своих аргументов,
вычисляются с помощью универсальной
замены переменной
,
где
-
рациональная функция своих аргументов,
вычисляются с помощью универсальной
замены переменной
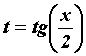 .
При этом
.
При этом . Однако универсальная замена обычно
связана с большими вычислениями, поэтому
в некоторых случаях можно ее избежать.
. Однако универсальная замена обычно
связана с большими вычислениями, поэтому
в некоторых случаях можно ее избежать.
Интегралы
вида
![]() вычисляются
с помощью замены
вычисляются
с помощью замены
![]() .
Интегралы вида
.
Интегралы вида
![]() вычисляются
с помощью замены
вычисляются
с помощью замены
![]() .
Интегралы вида
,
если
.
Интегралы вида
,
если
![]() ,
то есть четная рациональная функция
своих аргументов вычисляются с помощью
замены
,
то есть четная рациональная функция
своих аргументов вычисляются с помощью
замены
![]() .
.
Интегралы
вида
![]() вычисляются
с помощью формул понижения степени
вычисляются
с помощью формул понижения степени
 .
.
6.определенный интеграл и его свойства.
Пусть функция f(x) на отрезке [a;b]. Разобьём отрезок на n произвольных частей точками.
a=x1<x2...<Xi...<Xn=b. Точки, разделяющие отрезок [a;b] на частичные отрезки [Xi;Xi+1]
будем называть точками разбиения ∆Хi=Xi+1-Xi. В каждом из частичных отрезков
выберем произвольную точку φi
Xi≤Ψi≤Xi+1
Образуем сумму произведений (δ): n
δ=f(Ψi)ΔX1+f(Ψ2)ΔX2+...+f(Ψi)ΔX=∑f(Ψi)ΔXi , будем называть
i=1
интегральной суммой

интегральная сумма – сумма площадей прямоугольников с основанием ΔXi , с высотой
f(Ψi)
обозначим за λ=max{λΔXi)
конечный предел (I) интегральной суммы ∑ при λ , стремящейся к нулю, если он существует, называется определённым интегралом от ф-ции f(x) по
отрезку [a;b]
I=lim∑f(Ψi)ΔXi
λ→0 в
определённый интеграл обозначается символом ∫ f(x)dx= limf(Ψi)ΔXi
а λ→0
величина определённого интеграла не изменяется от обозначения переменной интегрирования
в в
∫f(x)dx=∫f(t)dt
а а
теорема (необходимое условие интегрируемости функции): интегрируемая на отрезке [a;b]
функция f(x) ограничена на этом отрезке (обратное утверждение не верно).
Если ф-ция f(x) непрерывна на отр. [a;b], то она интегрируема
Основные свойства определённого интеграла.
0
1. ∫f(x)dx=0
0
b a
2. ∫f(x)dx= - ∫f(x)dx
a b
для любых a,b,c
b c b
3. ∫f(x)dx= ∫f(x)dx + ∫f(x)dx
a a c
b b
4. ∫kf(x)dx = k∫f(x)dx
a a
b b b
5. ∫ (f(x)+-g(x))dx= ∫f(x)dx+-∫ g(x)dx
a a a
b
6. ∫ dx = b-a
a
b
7. если f(x)>= 0 , то ∫ f(x)dx>=0
a
b b
8. если на [a;b] выполняется неравенство: f(x)≤g(x) ,то ∫f(x) ≤ ∫g(x)dx
a a
9. наименьшее значение m, то наибольшее значение y=f(x) на отр [a;b], тогда выполняется
b
двойное неравенство: m(b-a)≤ ∫f(x)dx ≤ M(b-a)
a
7.формула Ньютона – Лейбница.
Теорема: пусть ф-ция y=f(x) непрерывна на [a;b]. F(x) – первообразная для f(x); тогда
B b
∫f(x)dx = F(x)│= F(b)-F(a) . ометим ещё два варианта данной формулы
A a
b
∫F’(x)dx = F(b)-F(a)
a
8.Методы интегрирования определенных интегралов
1)интегрирование по частям в определённом интеграле
b b b
∫udv = uv │ - ∫ vdu
a a a
2)замена переменной в определённом интеграле.
Теорема: пусть функция y=f(x) непрерывна на отр [a;b]. А функция X = φ(t) определена на отр [α;β] и имеет непрерывную производную внутри этого отрезка. Причём φ(α)= а,
b β
φ (β)=b. Тогда ∫f(x)dx = ∫f(φ(t))* φ’(t)dt
a α
9.Несобственные интегралы 1 и 2 рода. Признаки сравнения.
По теореме существования для функции
y=f(x) кусочно-непрерывной на интервале
[a,b], . определенный интеграл
![]() существует. Если функция y=f(x) неограничена
на [a,b] или интервал [a,b] неограничен, то
введенное нами понятие определенного
интеграла неприменимо. Тем не менее
необходимость работы с интегралами и
для этих случаев на практике возникает.
Но при работе с такими интегралами
нужно быть осторожными.
существует. Если функция y=f(x) неограничена
на [a,b] или интервал [a,b] неограничен, то
введенное нами понятие определенного
интеграла неприменимо. Тем не менее
необходимость работы с интегралами и
для этих случаев на практике возникает.
Но при работе с такими интегралами
нужно быть осторожными.
Пример (неверный). Вычислить
![]()
Но подынтегральная функция положительна, верхний предел больше нижнего и, следовательно, интеграл должен быть положительным.
Поэтому эти случаи нужно рассмотреть отдельно.
7.1. Несобственные интегралы второго рода.
Пусть функция y=f(x) неограничена в окрестностях некоторых точек cÎ[a,b] и интервал [a,b] - конечный.
Определение. Несобственным интегралом второго рода называется выражение
![]() (1)
(1)
Определение. Если существует предел выражения (2) при e®0, то говорят, что интеграл (1) сходится и этот предел является значением интеграла (1). Обозначается
![]() (3)
(3)
Определение. Если предел выражения (2) при e®0 не существует или равен бесконечности, то говорят, что интеграл (1) расходится.
Если предел выражения (2) при e®0 равен бесконечности, то пишут
![]()
Аналогично рассматривается случай, когда точка c единственная и совпадает с левым концом интервала c =a. Тогда при d>0 формула (3) запишется в виде:
![]()
Если точка c единственная и лежит внутри интервала [a,b], то
![]()
Если таких точек несколько, то нужно исследовать каждую точку в отдельности.
7.2. Несобственные интегралы первого рода.
Пусть функция y=f(x) определена на бесконечном интервале [a,¥) и ограничена на любом конечном интервале [a,b].
Определение. Несобственным интегралом первого рода называется выражение
![]() (4)
(4)
Определение. Если существует предел выражения (2) при b®¥, то говорят, что интеграл (4) сходится и этот предел является значением интеграла (4). Обозначается
![]() (5)
(5)
Определение. Если предел выражения (5) при b®¥ не существует или равен бесконечности, то говорят, что интеграл (4) расходится.
Если предел выражения (5) при b®¥ равен бесконечности, то пишут
![]()
Аналогично рассматривается случай
![]() и
и ![]()
Пример. Вычислить
![]()
10.Геометрическое приложение определенного интеграла.
1.Вычисление площади плоской фигуры в декартовых координатах.
B
S=∫f(x)dx
a
2.Для функции заданной параметрически
Y=Ψ(t)
X=φ(t) t1≤t≤t2
b t2
S=∫f(x)dx = ∫ Ψ(t)*φ’tdt
a t1
dx=φ’(t)dt
x=acost
y=bsint
3.Если кривая задана в полярной системе координат.
Псть кривая MN задана в полярной системе координат, причём ‘ро’(φ) неотрицательна на[αβ]. Криволинейным сектором, называется плоская фигура, ограниченная линией
Ρ(φ) и направленными от полярной оси под углами α и β.
Путём разбиения отрезка от α до β на частичные отрезки и приближения отдельных доль
Β 2
S=1/2 ∫ρ (φ)dφ
Α
4.Вычисление длины дуги плоской кривой.
L=liml= ∫√1+(f’(x))dx
x→0 a
длина дуги заданна Параметрически
x=ρcosφ
y=ρsinφ
β
L = ∫√(ρ(φ)^2+(ρ’(φ))^2)dφ
Α
5.Вычисление объёма тела вращения.
Пусть функция y=f(x) непрерывна и неотрицательна на отрезке [A;B]. Тогда тело, которое образуется при вращении вокруг оси Ох криволинейной трапеции aAbB имеет объём
b 2
Vx= π∫ f (x)dx
a
d 2
если вокруг Оу, то Vy=π∫ φ (y)dy
c
площадь поверхности вращения
пусть f(x) неотрицательна и имеет непрерывную производную.
6. Площадь поверхности образованной вращением вокруг оси Ох , вычисляется по формуле:
b 2
P=2π ∫ f(x) √1+(f’(x))
a
если кривая задана в параметрическом виде, то
β 2 2
P=2π ∫ y(t) √ (y’(t)) + (x’(t)) dt
β 2
если кривая в полярных координатах, то P=2π ∫ ρ(φ)sinφ*√ (ρ(φ)) +ρ’(φ) dφ
α
11.Формулы приближенного вычисления определенного интеграла.
Формула средних прямоугольников
![]()
![]()
![]()
![]()
Формула трапеций
![]()
![]()
![]()
12.Определение двойного интеграла. Геометрический смысл. Основные свойства.
Если интегрируемая сумма (которая сверху) имеет предел при альфа -> 0, то этот предел называется двойным интегралом для функции f(x;y) по области Р.
Двойной интеграл f(x;y)dS или дв.инт. f(x;y) dxdy
Геометрический смысл двойного интеграла: V=дв.инт f(x;y) dxdy
Теорема: Если функция f(x;y) непрерывна в замкнутой ограниченной области, то она интегрируема в этой области как и для случая функции одной переменной, класс интегрируемости (?!) функций оказывается более широким, чем класс непрерывности (?!) функций.
Теорема: Пусть функция f(x;y) ограничена в замкнутой ограниченной области Р и имеет разрывы лишь на конечном числе кривых этой области, которые являются графиками непрерывных функций y=g(x); x=h(y), тогда функция f(x;y) интегрируема в области Р.
Свойства двойного интеграла - Аналогичны свойствам определенного интеграла(7 штук).
Вычисление:
Теорема: Пусть f(x;y) определена и интегрируема в области Р, ограниченной снизу и сверху двумя непрерывными кривыми y=y1(x); y=y2(x) y1<=y<=y2 a<=y<=b
Пусть также для каждого х принадлежащего [a;b] существует определенный интеграл по dy, тогда существует его повторный интеграл от а до в.
Если функция ограничена слева и справа – тогда x=x1(y); x=x2(y) x1<=x<=x2 c<=x<=d
