11. Найменше і найбільше значення функції в замкненій області.

Нехай у замкненій обмеженій області задана диференційована функція . Диференційована функція є неперервною, отже за теоремою Вейерштрасса вона досягає в області як свого найбільшого, так і свого найменшого значення (іноді кажуть «глобального максимуму» і «глобального мінімуму»). Задача полягає в тому, щоб знайти точки, в яких досягається найбільше і найменше значення функції і самі ці значення.

Якщо глобальний екстремум досягається у межовій точці області, то ця точка є або особливою точкою межі або точкою умовного екстремуму функції при умові рівняння межі (контура) області . Особливими точками межі є зокрема точки стикування ділянок межі, заданих різними рівняннями.

Наведені міркування дозволяють сформулювати такий алгоритм розв’язання поставленої задачі:

1. Знайти критичні точки функції , що лежать всередині області , і обчислити значення функції в цих точках (не вдаючись до дослідження на екстремум);

2. Знайти критичні точки умовного екстремуму на межі області і обчислити значення функції в цих точках і в особливих точках межі;

3. Порівняти отримані значення : найбільше з них і буде глобальним максимумом, а найменше – глобальним мінімумом функції в області .

Приклад.

Знайти найбільше і найменше значення функції

в області , обмеженій лініями

(рис. 9.16)

1) Знаходимо критичні точки

Р И С 9.16 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1

Маємо одну критичну точку , яка знаходиться всередині області. Значення функції в цій точці .

2) Межа області складається з трьох ділянок:

Знайдемо критичні точки умовного екстремуму на кожній ділянці. Для цього скористаємося методом виключення (підстановки), оскільки рівняння в’язей (ділянок межі) мають дуже простий вигляд.

а) Ділянка . Підставляємо у вираз функції:

.

Знаходимо критичну точку умовного екстремуму:

,

отже критична точка . Значення функції в цій точці .

б) Ділянка . Аналогічно до попереднього:

, отже критичною є точка . В цій точці значення функції .

в) Ділянка . З рівняння вязі виражаємо і підставляємо в вираз цільової функції

.

.

Критична точка . Значення функції в цій точці .

г) ?? Особливими точками межі є точки . Значення функції в цих точках: .

3) Порівнюючи між собою отримані значення цільової функції в точках , робимо висновок, що найменше значення досліджуваної функції досягається в точці , а найбільше – в точці .

11. Приклади і вправи.

Задача 1. Побудувати області , задані нерівностями:

а) .

б) .

Розв’язання.

а) Заміняючи нерівності рівностями, отримаємо рівняння ліній, з яких складається межа області :

еліпс з півосями ;

еліпс з півосями

вісь ; пряма, що проходить через початок координат з кутовим коефіцієнтом (рис. 9.17).

Р И С 9.17 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Ці лінії розбивають площину на кілька частин, і залишається визначити координати точок якої частини задовольняють задані нерівності. В даному випадку нерівність означає, що точки заданої області лежать у верхній півплощині, включаючи вісь , а нерівність означає, що ці точки розташовані нижче прямої і на самій цій прямій. Ці умови визначають кут у першому квадранті, утворений додатною піввіссю і прямою . В свою чергу еліпси розбивають цей кут на частини – (Рис. 9.17). Беручи по одній точці в кожній з цих частин, перевіряємо, чи задовольняють координати цих точок нерівності

.

Точка , для неї , отже .

Точка , для неї , водночас ,

отже точка .

Точка , для неї , отже .

Таким чином заданою областю є область , включаючи її межу (область замкнена). На рис. 9.17 область заштрихована.

б) Запишемо рівняння ліній, які утворюють межу області:

.

Лінії і обмежують смугу одиничної ширини у верхній півплощині, а нерівності означають, що точки області розташовані всередині цієї смуги і на її межах. В свою чергу згадана смуга розбивається на три частини лініями та . Підставляючи координати точок, ? взятих в кожній з цих частин у нерівності , переконуємося, що область є частиною, розташованою поміж лініями та (заштриховано на рис. 9.18), включаючи її межу.

Задача 2. Знайти природну область визначення функції

а) б)

Розв’язання .

а) Для того, щоб мала дійсне значення, потрібно, щоб під коренями стояли невід’ємні величини, тобто і повинні задовольняти нерівності .

Ці нерівності і описують область визначення функції. З першої нерівності випливає, що ця область розташована у правій півплощині площини , а з другої (що вона розташована нижче кривої (верхньої вітки параболи . Шукана область зображена на рис. 9.19.

Р И С 9.19 !!!!!!!!!!!!!!!!!!!!!!!!!!!11

б) Функція визначена на відрізку , тому для існування функції потрібно, щоб аргументи і задовольняли нерівності і .

Отже межа шуканої області утворена прямими лініями:

.

Безпосередньо пересвідчуємося, що потрібні нерівності задовольняють координати внутрішніх і межових точок паралелограма, сторони якого лежать на вказаних прямих. Це і є область визначення заданої функції (рис. 9.20).

Р И С . 9.20. !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1

Задача 3. Знайти лінії рівня функції

а) б) .

Розв’язання. а) Рівняння лінії рівня функції має вигляд , де стала величина. Надаючи їй різних числових значень, отримуємо рівняння різних ліній рівня. В даному разі рівняння лінії рівня , або . Таким чином система ліній рівня даної функції є сім’я парабол (рис. 9.21).

Р И С. 9.21 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

б) Для даної функції рівняння лінії рівня має вигляд .

З’ясуємо, яку лінію визначає це рівняння, для чого виконаємо ряд перетворень.

Перенесемо у праву частину: .

Піднесемо обидві частини до квадрата: .

Квадрати у лівій і правій частині взаємно знищуються, і ми отримуємо:

.

Це є сім’я парабол з вершинами у точці і параметром, рівним (рис. 9.22), вітки яких спрямовані вліво.

Р И С. 9.22 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1

Задача 4. Знайти частинні похідні заданих функцій по всіх аргументах:

а) ; б) .

Розв’язання.

а) Задану функцію зручно подати як різницю логарифмів:

.

Для отримання диференціюємо, вважаючи сталою величиною:

.

Вважаючи сталою величиною, знаходимо

б) .

Диференціюємо по : (похідна по дорівнює 0).

Аналогічно .

.

Задача 5. Знайти повний диференціал функції .

Розв’язання. Знаходимо частинні похідні: .

Тоді

.

Задача 6. Обчислити наближено, використовуючи повний диференціал функції

.

Розв’язання. Розглянемо функцію

і покладемо ,

тоді За формулою (9.8)

.

Знаходимо частинні похідні:

.

Тоді

.

Задача 7. Знайти похідну , якщо .

Розв’язання.

.

За формулою (9.11):

.

Задача 8. Знайти похідну функції , заданої неявно рівнянням

.

Розв’язання.

Нехай . Тоді

Згідно з формулою (9.14)

Задача 9. Знайти градієнт функції у точці і похідну цієї функції в точці за напрямом вектора .

Розв’язання. Знаходимо частинні похідні заданої функції:

і обчислюємо їх значення в точці :

.

Тоді за формулою (9. 19) .

Знаходимо напрямні косинуси вектора :

.

Тоді

.

Похідну за напрямом обчислюємо за формулою (9. 18):

.

Задача 10. Написати рівняння дотичної площини і нормалі в точці до поверхні . . ??????????????

Нехай . Тоді:

Обчислюємо значення частинних частинних похідних у точці :

.

За формулою (9.23) записуємо рівняння дотичної площини:

.

Після скорочення на і розкриття дужок: .

Нормаль – пряма , яка перпендикулярна до дотичної площини і проходить через точку дотику, отже рівняння нормалі

.

Задача 11. Довести, що функція задовольняє рівняння .

Знаходимо ча0стинні похідні:

Підставимо в рівняння:

, що й треба було довести.

Задача 12. Дослідити на екстремум функцію .

Розв’язання. Знаходимо стаціонарні точки функції:

Розв’язуючи цю систему, отримуємо чотири стаціонарні точки:

.

Для перевірки виконання достатньої умови екстремуму знаходимо частинні похідні другого порядку і записуємо дискримінант .

.

В точці маємо , екстремуму немає.

В точці : , при чому , значить точка є точкою мінімуму функції і .

В точці : , екстремуму немає.

В точці : , екстремуму немає.

Таким чином досліджувана функція має єдиний локальний екстремум (мінімум) у точці , який дорівнює .

Задача 13. На вітці кривої , розташованій у першому квадранті, знайти точку, найближчу до прямої .

Розв’язання. Нехай точка кривої . Її відстань від прямої дорівнює . Для зручності будемо шукати мінімум не самої відстані, а величини, пропорціональної її квадрату. Отже цільовою функцією буде при рівнянні в’язі .

Отже маємо задачу на умовний екстремум.

Складаємо функцію Лагранжа:

.

Необхідні умови екстремуму:

Щоб виключити , помножимо перше рівняння на , а друге на і додамо:

або

.

Розглянемо два випадки.

а) Якщо , то . Підставляючи у третє рівняння, одержимо або

Одержане рівняння не має дійсних коренів. Справді, ліва частина приймає додатні значення лише в інтервалі ( 0; 1). У цьому інтервалі і , отже і для всіх , тоді як права частина рівняння . Таким чином даний випадок критичних точок не дає.

б) Якщо , то . Підставимо у рівняння в’язі:

або .

Отримуємо два значення: і , звідки . Це дає нам дві критичні точки: і .

Але точка належить до тієї ж вітки кривої , яка розташована у квадранті, отже умову задачі не задовольняє. Таким чином маємо єдину критичну точку , яка і є шуканою точкою мінімуму цільової функції, тому що саме існування мінімуму випливає з геометричного змісту задачі.

Задача 14. Знайти найбільше і найменше значення функції

в області, обмеженій лінією .

Розв’язання. Задана область є круг з центром у початку координат і радіусом .

Р И С 9.23 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Знаходимо критичні точки функції :

Маємо єдину критичну точку , яка розташована всередині області. Значення цільової функції в цій точці

Знаходимо критичні точки умовного екстремуму на контурі області. Складемо функцію Лагранжа:

і відшукаємо її критичні точки:

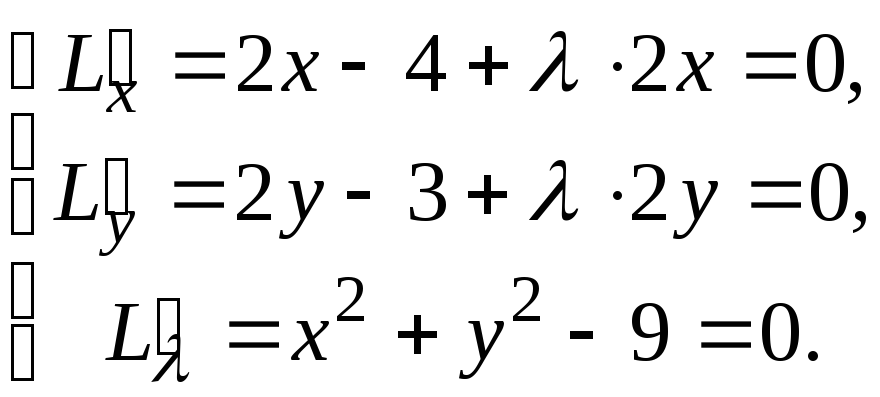
Помножимо почленно перше рівняння на , друге на і додамо. Одержимо звідки . Підставимо у рівняння в’язі:

Тоді .

Одержали дві критичні точки: і . Значення у цих точках: ; .

Отже задана функція досягає свого найбільшого значення в точці , а найменшого значення в точці .

Вправи.

1. Побудувати області, задані нерівностями:

а) .

б) .

Відповіді: а) рис. 9.24; б) рис. 9.25.

РИС, 9.24 Рис. 9.25 !!!!!!!!!!!!!!!!!!!!!!!

2. Знайти природну область визначення функції:

а) ; б) .

Відповіді: Області описуються нерівностями:

а) при і при

б) .

3. Знайти частинні похідні даних функцій по кожному з аргументів:

а) ; б) .

Відповіді: а) .

б)

.

4. Знайти повний диференціал функції .

Відповідь: .

5. Обчислити наближено, використовуючи повний диференціал функції

.

Відповідь: .

6. Знайти повні похідні , якщо

а) . б) .

Відповіді:

а) .

б) .

7. Знайти похідну функції , заданої неявно рівнянням:

а) б) .

Відповіді:

а) ; б) .

8. Знайти градієнт функції в точці і похідну цієї функції в точці за напрямом вектора .

Відповідь: , .

9. Написати рівняння дотичної площини і нормалі в точці до поверхні .

Відповідь:

.

10. Знайти повний диференціал другого порядку функції .

Відповідь:

.

11. При якому значенні сталої функція задовольняє рівняння ?

Відповідь: .

12. Дослідити на екстремум функцію .

Відповідь: .

В стаціонарних точках і екстремуму немає.

13. Знайти умовний екстремум функції при умові .

Відповідь: .

14. Знайти найбільше і найменше значення функції в області, заданій нерівністю .

Відповідь: ;

.

45