24. Понятие дроби и рационального числа.

Дроби: Каждую из равных частей, на которые можно разделить элементы будем называть долей. Каждый элемент будем называть единицей. Определение: дробью или дробным числом называется пара натуральных чисел a,n, характеризующихся мн А одинаковых долей единицы. Первое из них (а) показывает, сколько долей содержит мн А и называется числителем дроби. Второе (n) – на сколько одинаковых долей разделена единица – это знаменатель. Числитель и знаменатель называются членами дроби. Запись дроби: , где а и n – N числа и n>1. Если 0:n=0, то это пустое множество долей. Если a:1=a, то есть доли элементов представляют собой сами элементы. Дробь 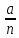, где а-(, а n-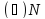, называется обыкновенной дробью. Если a<n, то дробь называется правильной. Если наоборот, то неправильной. N число вместе с правильной дробью называется смешанным числом (3). Рациональные числа: Отношение равенства является отношением эквивалентности на множестве дробей, поэтому оно порождает на нем классы эквивалентности. В каждом таком классе содержатся равные между собой дроби. Например, множество дробей  - это один класс, множество дробей 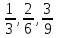...это другой класс и т.д. Дроби одного класса выражают длину одного и того же отрезка. Но длина отрезка должна представляться единственным числом. Поэтому считают, что равные дроби - это различные записи одного и того же положительного рационального числа. Определение: Положительным рациональным числом называется класс равных дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление) этого числа. Например, о дроби 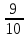мы должны говорить, что она является за­писью некоторого рационального числа. Однако часто для краткости говорят: - это рациональное число. Множество всех рациональных чисел принято обозначать символом Q.

26. Свойства множества рациональных чисел (q)

1. В результате арифметических операций над рациональными числами (сложение, умножение, вычитание, деление, кроме деления на ноль) получается рациональное число. 2. Множество рациональных чисел упорядочено, то есть для любой пары рациональных чисел a и b либо a<b либо a>b. 3. Множество рациональных чисел плотно, то есть для любой пары рациональных чисел a и b существует такое рациональное число c, что a<b<с. Очевидно, что таких чисел бесконечное множество.

28. Рациональные числа как бесконечные десятичные периоды дроби

Всякое положительное рациональное число всегда можно представить в виде десятичной дроби: либо конечной, либо бесконечной периодической. Например: 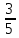=0,6; =0,333...=0,(3). =,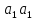...........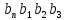 ....... - называется периодом десятичной дроби, где не все 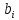=0. Заметим, что конечная дробь может быть записана в виде бесконечной периодической с нулем в периоде. 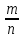=,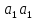…≠0. Однако, чаще встречается другое представление рациональных чисел в виде десятичной дроби: . 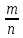=,… 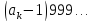-Q- 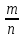− записываются в виде десятичного разложения рационального числа вида 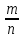, взятого с противоположным знаком. Число 0 представляется в виде 0,000. Таким образом, всякое рациональное число всегда представимо в виде бесконечной десятичной периодической дроби не содержащей 0 в периоде, кроме самого числа 0. Такое представление единственное.

Рассмотрим целое число 5, обыкновенную дробь 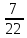 и десятичную дробь 8,377. Целое число 5 можно записать в виде бесконечной десятичной дроби: 5,0000... Десятичную дробь 8,377 также можно записать в виде бесконечной десятичной дроби: 8,377000... Для числа воспользуемся методом «деления углом»: начиная со второй цифры после запятой происходит повторение одной и той же группы цифр: 18, 18, 18, ... . Таким образом, 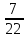= 0,3181818... Короче это записывают так: 0,3(18). Повторяющуюся группу цифр после запятой называют периодом, а саму десятичную дробь — бесконечной десятичной периодической дробью. Для этого надо в периоде записать число 0: 5 = 5,00000... = 5,(0). Так же обстоит дело и с числом 8,377: 8,377 = 8,377000... = 8,377(0). Чтобы все было аккуратно, говорят так: 8,377 — конечная десятичная дробь, а 8,377000... — бесконечная десятичная дробь. Таким образом, и число 5, и число , и число 8,377 удалось записать в виде бесконечной десятичной периодической дроби. Вообще, любое рациональное число можно записать в виде бесконечной десятичной периодической дроби.