16. Определение произведения, в основе которого лежит понятие суммы нескольких слагаемых.

Теорема: Если число b>1, то произведение чисел a и b равно сумме b слагаемых, каждое из которых равно a. a*1=1, a*0=0. Определение умножения: если a и b - 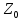, то a*b называется числом, удовлетворяющим следующим условиям: 1) а*b=a+a+….a, где a+a+….a используется b раз и b>1. 2) a*b=a, если b=1. 3)a*b=0, если b=0. 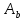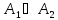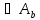Свойству 1 из определения можно дать следующую т-м трактовку: если мн , … содержит по а элементов каждое, причём никакие 2 из них не пересекаются, то их объединение … содержит a*b элементов. С т-м позиции произведение a*b при b>1 представляет собой число элементов в объединении B множеств, каждое из которых содержит по a элементов и никакие 2 из них не пересекаются. a*b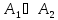=n(…, если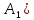 n(=n()…n(=a и каждое из них попарно не пересекаются.

18. Теоретико-множественный смысл правил деления суммы и произведения на число.

Используя теоретико-множественный подход к действиям над целы­ми неотрицательными числами, можно дать теоретико-множественное истолкование правила деления суммы на число: если частные а:с и b:с существуют, то (а +b):с = а:с + b:с. Пусть а =n(А) и b =n(В), причем А  В =. Если множества А и В можно разбить на равночисленные подмножества, состоящие из с элементов каждое, то и объединение этих множеств допускает такое же разбиение. Если при этом множество А состоит из а:с подмножеств, а множество В – из b:с подмножеств, то А  В состоит из а:с + b:с подмножеств. Это и значит, что(а + b ):с =а:с + b:с. Аналогично проводятся рассуждения и в случае, когда с рассмат­ривается как число равночисленных подмножеств в разбиении мно­жеств А и В.

20. Определение арифметических действий над числами, рассматриваемых как мерами отрезков.

Если отрезок а составлен из отрезков в и с и мера отрезков в при единичном отрезке е=1 m_eb =p, m_ec =q, то m_ea = p+q=m_eb + m_ec. Доказательство: m_eb =p => b=pe, m_ec=q => c=qe, тогда отрезок а разбит на p+q отрезков, каждый из которых = е, т.е. a=(p+q)e => m_ea = p+q. Вывод: сумма 2 натур-ых чисел p и q = мере отрезка а, который состоит из отрезков b и c, меры кот-ых при одной и той же единице длины = p и q соответственно. Если мера отрезка а при единице длины e=p, a m_e1e = q => m_e1a = pq. Доказательство: m_ea=p => a=pe, m_e1=q => e=q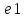 => отрезок а будет составлен из pq отрезков 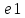, т.к. каждый отрезок e составлен из q 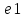, всего отрезков ep => m_e1a = q+q+…+q=pq. 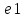Вывод: при переходе к более мелкой единице измерения, вычисляя меру отрезка а при новой единице измерения выполняется действие умножения, т.е умножение N чисел отражает переход к новой единице длины: если N число p мера отрезка а при единице длины е, а N число q мера отрезка е при единице длины , то произведение pq является мерой отрезка а при единице длины .Пусть a=b+c, m_ea =p, m_eb = q, тогда m_ec = p-q. Вывод: разность 2х натуральных чисел p и q, где p мера отрезка а при единице длины е, а q мера отрезка b при единице длины е = m_ec, которая является дополнением отрезка b до отрезка а. m_ea=p, m_ee1=q, m_e1a=p:q. Вывод: операция деления натуральных чисел отражает переход новой единицы длины к более крупной: если p это мера отрезка а при единицы длины е, а q это мера отрезка е1 при единице длины е, то мера отрезка а при единице длины е1 =p:q.

22. Краткие исторические сведения о возникновении понятия «дробь» и отрицательного числа. О древности понятия "половина" свидетельствует тот факт, что во всех языках оно имеет особое наименование, не происходящее от слова "два". Выражения "большая половина", "меньшая половина" первоначально означало одну из двух частей (не обязательно равных друг другу).  Первые представления о целом числе возникли в процессе счёта; первые представления о дробях — из процесса измерения (длин, площадей, веса и так далее). Следы исторической связи исчисления дробей и системы мер можно обнаружить у многих народов. Так, в вавилонской системе мер веса (и денег) 1 талант составлял 60 мин, а одна мина — 60 шекелей. Соответственно с этим в вавилонской математике широко употреблялись шестидесятеричные дроби. В древнеримской весовой (и денежной) системе 1 асс делился на 12 унций; сообразно с этим римляне пользовались двенадцатеричными дробями. Дробь, которую мы называем 1/12, римляне именовали "унцией", хотя бы она употреблялась для измерения длины или иной величины; дробь, которую мы называем 1/8, римляне называли "полторы унции" и тому подобное.  Наши "обыкновенные дроби" широко употреблялись древними греками и индийцами. Правила действий с дробями, изложенные индийским учёным Брамагуптой (8 век н. э.), лишь немногим отличаются от наших. Наша запись дробей тоже совпадает с индийской; только дробной черты индийцы не писали; греки записывали сверху знаменатель, а снизу числитель, но чаще пользовались другими записями. Индийское обозначение дробей и правила действий над ними были усвоены в 9 веке в мусульманских странах благодаря узбекскому учёному Мухаммеду Хорезмскому (аль-Хваризми). Они были перенесены в Западную Европу итальянским купцом и учёным Леонардо Фибоначчи из Пизы (13 век). Наряду с "обыкновенными" дробями до 17 века применялись (преимущественно в астрономии) шестидесятеричные дроби. Они были вытеснены десятичными дробями, введёнными голландским купцом и выдающимся инженером-учёным Симоном Стевином (1548—1620). История возникновения отрицательных чисел начинается в VII веке в Китае и Индии. Только тогда они назывались не «отрицательными числами», а были «долгами» или «недостачей». В Европе об отрицательных числах первым написал Леонард Пизанский в своей «Книге абака» в 1202 году. Изначально они также трактовались, как долг. Но даже несмотря на это в XVII такой знаменитый ученый как Паскаль считал, что если из ноля вычесть какое-либо положительное число, то в результате получится ноль. История возникновения отрицательных чисел получила свое развитие с появлением аналитической геометрии. Теперь они наравне с положительными были представлены на геометрической оси. В 1831 году Гаусс полно обосновал, что отрицательные числа абсолютно равнозначны по правам с положительными, а то, что их можно применить не во всех случаях, значения не имеет. История возникновения отрицательных чисел заканчивается в XIX веке, когда Уильям Гамильтон и Герман Грассман создали полную теорию отрицательных чисел. С этого момента начинается история развития данного математического понятия.