8. Определение деления с остатком

Определение – пусть a и b – N числа. Неполным частным q с остатком r при делении a на b называются такие 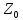, что a=bq+r , причём 0<r<b.

Теорема: 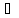Nчисел a и b существуют q и r такие, что a=bq+r, причём 0<r<b. Другой пары (q и r) c тем же свойством не существует.

10. Метод математической индукции

Данный метод основан на аксиоме Пеано №4 (пусть мн M есть подмножество множества N, и известно, что: а) единица содержится в M, б) из того, что a содержится в M => что и а’ содержится в М, тогда мн М совпадает с множеством N). Теорема: если утверждение А(n) с N переменной n истинно для n=1 и из того, что оно истинно для n=K’, то утверждение A(n) – истинно для любого N числа n.

Доказательство. Обозначим через М множество тех и только тех натуральных чисел, для которых утверждение А(n) истинно. Тогда из условия теоремы имеем: 1) 1М; 2) k M k’ M. Отсюда, на основании аксиомы 4, заключаем, что М = N, т.е. утверждение А(n) истинно для любого натурального n. Метод доказательства, основанный на этой теореме, называется методом математической индукции. Такое доказательство состоит из двух частей: 1) доказывают, что утверждение А(n) истинно для n = 1, т.е. что истинно высказывание А(1); 2) предполагают, что утверждение А(n) истинно для n = k, и, исходя из этого предположения, доказывают, что утверждение A(n) истинно и для n = k + 1, т.е. что истинно высказывание A(k)  A(k + 1). Если А(1)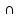А(k)  A(k + 1) – истинное высказывание, то делают вывод о том, что утверждение A(n) истинно для любого натурального числа n.

12. Порядковые и количественные n числа, примеры.

Одно и тоже мн А не может быть взаимно-однозначно отображено на 2 различных отрезках N ряда чисел. Т.е. каждому конечному мн А может быть поставлено в соответствии такое число А, что мн А взаимно-однозначно отображается на отрезок N ряда 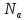, где a- называется число элементов во мн А и записывается n(A)=a. Полученное a в этом смысле называется количественное N число. Порядковые N числа выражаются числительными (первый, второй). При счёте числа обладают рядом свойств: располагаются в определенном порядке, должно существовать первое число и т.п.

14. Теоретико-множественный смысл разности.

В аксиоматическом подходе вычитание записывается так: а-b=c (. Теорема: Пусть А - конечное множество и B его собственное подмножество, тогда мн A\B тоже конечно, причём выполняется равенство n(A\B)=n(A)-n(B). С теоретико-множественной позиции разность N чисел a и b представляет собой число элементов в дополнении подмножества B до мн A, если : a=n(A), b=n(B), то B явл.подмножеством A: a-b=n(A)-n(B)=n(A\B), a-0=a:n(A\)=n(A)=a, a-a=0::n(A\A)=n()=0. С т-м позиции a<b на с или (b>a на c) означает, что если а=n(A), а b=n(B), то в мн В содержится столько же элементов, сколько в мн А и еще с элементов. Взаимосвязь действий над множествами с действиями над числом и т-м смысл отношений «меньше на» и «больше на» позволяют обосновать выбор действий при решении задач с этими отношениями. Пример: на столе 5 чашек, а ложек на 2 меньше. Сколько на столе ложек? 2 мн: чашки(А) и ложки (В). n(B)=n(A)-2=5-2-3.