2. Основные гипотезы
Рассмотрим длинную
замкнутую
(
),
вообще говоря, подкрепленную цилиндрическую
оболочку. Отнесем ее к декартовой системе
отсчета
,
ось
которой параллельна образующим оболочки,
а оси
,
принадлежат плоскости ее дальнего (
)
торцевого поперечного сечения (см. рис.
2, где
замкнутая
и, вообще говоря, подкрепленная оболочка
представлена условно гладкой трехзамкнутой
оболочкой).
Тело оболочки
ограничено, с одной стороны, внешней и
внутренними цилиндрическими поверхностями,
а с другой стороны, — торцевыми поперечными
сечениями
(
)
и
(
).
Площадь
произвольного поперечного сечения —
связная
плоская область, заключенная между
линиями пересечения цилиндрических
поверхностей с плоскостью сечения. Для
задания геометрии оболочки необходимо
задать уравнения этих кривых, совпадающих
с уравнениями соответствующих
цилиндрических поверхностей.
Декартовая
система отсчета
удобна при описании деформирования
оболочки как балки (стержня). В тех
случаях, когда необходимо рассмотрение
формы оболочки или ее поперечного
сечения, более предпочтительной
оказывается так называемая нормальная
система отсчета.
Она
отличается от декартовой
тем, что в ней вместо координат
,
используются нормальная координата
,
отсчитываемая в направлении единичной
внешней нормали
к срединной поверхности оболочки, и
естественный параметр
контура
ее поперечного сечения (см. рис.3;
образуют правую систему отсчета).
Нетрудно понять, что если параметрические уравнения контура поперечного сечения (срединной поверхности) имеют вид
,
то декартовы координаты произвольной точки тела оболочки выражаются через нормальные , формулами
.
Здесь
,
,
где
,
и
— отличные от нуля (
)
направляющие косинусы нормали
и единичной касательной
контура поперечного сечения (см. рис.
3). Кроме того, начиная отсюда, мы
договариваемся производные функции
одного аргумента помечать вверху справа
от символа функции нужным количеством
штрихов.
У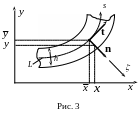
читывая,
что толщина оболочки мала по сравнению
с другими ее габаритными размерами,
примем следующее упрощающее предположение:
геометрия оболочки, ее смещения, деформации, напряжения и объемные внешние силы не меняются по толщине оболочки.
Это означает, что
геометрия и напряженно–деформированное
состояние оболочки всецело определяется
геометрией и напряженно–деформиро-ванным
состоянием ее срединной поверхности.
В частности, геометрию оболочки можно
считать заданной, если известны ее
толщина
и уравнение контура ее поперечного
сечения
Возможный отказ от принятого упрощающего предположения привел бы к неоправданному для тонких оболочек усложнению вычислений без ощутимого влияния на точность результатов.
В строгой постановке решение задачи о напряженно–деформированном состоянии длинной оболочки обречено на неуспех из–за неустранимой в рамках теории упругости неустойчивости вычислений, порождаемой малыми геометрическими параметрами. Справиться с нею удается лишь путем введения в теорию упругости дополнительных предположений, в той или иной мере ограничивающих деформирование оболочки в направлении этих параметров.
Будем предполагать, что стрингеры работают только на растяжение–сжатие, причем их упругие линии, принадлежащие срединной поверхности оболочки, деформируются так, как это предписывает обсуждаемая ниже ее (оболочки) модель. В таком случае стрингеры в поперечном сечении оболочки можно рассматривать как дополнительные сосредоточенные площади на контуре поперечного сечения, которые участвуют наряду с оболочкой в восприятии нормальных напряжений.
В дальнейшем нам не раз придется интегрировать по площади поперечного сечения стрингерной оболочки, представляющей собой кусочно-непрерывную функцию длины дуги контура поперечного сечения. С этой целью удобно воспользоваться интегралом Стилтьеса. Поясним его смысл.
Пусть
— функция дуги
контура поперечного сечения и пусть
— кусочно
непрерывная функция площади поперечного
сечения, где
— площадь поперечного сечения стрингера
,
— функция Хевисайда, определяемая
равенством
— дельта-функция
Дирака, обладающая, напомним, свойствами
(
)
,
а суммирование осуществляется по тем скачкам, которые попали в область интегрирования (на это указывает тильда над знаком суммы).
Очевидно,
что дифференциал
равен
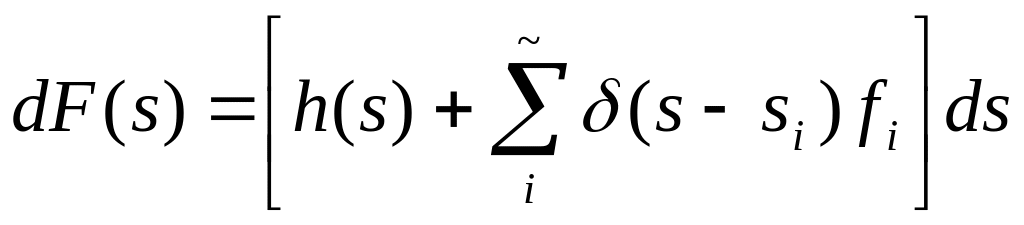
Тогда интеграл Стилтьеса определяется так
Малость размеров поперечных сечений оболочки по сравнению с ее длиной позволяет ввести следующие привычные для классической теории стержней (балок) гипотезы:
Гипотеза 1. Поперечные сечения оболочки в своей плоскости недеформируемы.
Гипотеза
2. В
осевом направлении (по оси
)
оболочка деформируется по закону
плоскости.
Гипотеза
3.
В
поперечном сечении оболочки возникают
только нормальные
и касательные
напряжения, не меняющиеся, как отмечалось,
по толщине оболочки, причем последнее
напряжение направлено всегда по
касательной к контуру поперечного
сечения.
Другие напряжения в виду их малости не учитываются.
В силу
гипотезы 2, если
— осевая деформация, то
и согласно закону Гука для нормального напряжения имеет место формула
|
(1) |
Здесь
,
,
— искомые величины,
где
— так называемая редукционная функция
по материалу, а
— модуль Юнга какого-то материала, за
который удобно принимать наиболее
распространенный в сечении материал.
Вместо
касательного напряжения
будем использовать поток касательных
сил (ПКС)
,
связанный с эти напряжением зависимостью
