Балочная теория оболочек

Балочная теория оболочек уже давно широко применяется в инженерной практике. И по сей день интерес к ней не ослабевает. Именно по этой причине теория эта прочно и вполне по праву завоевала место традиционного раздела курса строительной механики летательных аппаратов.

1. Исходные положения

Под оболочкой принято понимать криволинейное тело, один размер которого — толщина намного меньше других его характерных геометрических параметров. Поверхность, разделяющая толщину оболочки пополам, называется срединной поверхностью.

В зависимости от формы срединной поверхности различают цилиндрические, конические, сферические, тороидальные и прочие оболочки. Из иных классификаций отметим оболочки постоянной и переменной толщины, однослойные и многослойные, гладкие и подкрепленные ребрами в одном или двух направлениях, изотропные и анизотропные.

Общая теория оболочек — раздел прикладной механики деформируемого твердого тела, занимающийся анализом напряженно–деформированного состояния, вообще говоря, всех перечисленных и не перечисленных выше типов оболочек. В основе классической теории оболочек лежит гипотеза Кирхгоффа–Лява, согласно которой нормали к срединной поверхности оболочки в процессе ее деформирования ведут себя как абсолютно твердые прямые волокна. Другими словами, оболочка не деформируется в поперечном по отношению к ее срединной поверхности направлении.

Гипотеза Кирхгоффа–Лява отражает хорошо известный эмпирический факт: тело в направлении малого геометрического параметра деформируется слабо. Для оболочки роль такого параметра играет толщина, которая намного меньше габаритов оболочки и радиусов кривизны ее срединной поверхности.

Балочная теория оболочек предназначена для анализа напряженно--деформированного состояния длинных оболочек — оболочек, вытянутых в одном направлении и внешне напоминающих стержень. Основное требование, предъявляемое к этой теории по ее замыслу, — достоверная оценка напряжений, возникающих в поперечных сечениях оболочки — сечениях, перпендикулярных ее длине. Ниже мы ограничимся рассмотрением только цилиндрических оболочек постоянного поперечного сечения.

Пусть — толщина оболочки, и — наименьший и наибольший размер ее поперечного сечения, а — длина образующих (см. рис. 1.1, а). Тогда область применимости балочной теории оболочек описывается качественно неравенством

равносильным, очевидно, двум отношениям

Первое из них говорит о том, что изучаемое тело — оболочка. В силу второго отношения она является к тому же еще и стержнем (балкой). Чем сильнее эти отношения, тем точнее балочная теория оболочек. В количественном выражении область применимости балочной теории оболочек можно установить путем сопоставления полученных по ней числовых результатов либо с результатами решения той же задачи по более строгой, обходящейся меньшим количеством гипотез, теории, либо же с данными эксперимента.

Н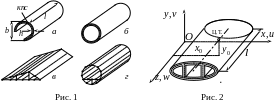 азовем линию пересечения срединной поверхности оболочки с плоскостью, нормальной к образующим, контуром поперечного сечения (кпс). В зависимости от его вида можно говорить об оболочках открытых, однозамкнутых и многозамкнутых. Их примеры показаны на рис. 1, где на рис. 1, а и б представлены соответственно открытая и однозамкнутая гладкие оболочки, а на рис. 1, в и г — схемы трехзамкнутых стрингерных оболочек типа крыла и фюзеляжа.