2.2. Достаточный признак геометрической неизменяемости

Чтобы установить для произвольно нагруженной стержневой системы ее геометрическую неизменяемость в широком смысле, достаточно убедиться в отсутствии возможности изменения положения системы в целом и взаимных смещений всевозможных ее фрагментов как абсолютно твердых тел. Эта самая общая формулировка достаточного признака является, по существу, перефразировкой определения геометрической неизменяемости. Воспользоваться ею непосредственно можно лишь при исследовании простейших стержневых систем. В остальных случаях немыслимость перебора всевозможных фрагментов стержневой системы, включая отдельные элементы ее, говорит о не конструктивности и, следовательно, об ограниченной практической полезности данной выше формулировки.

Заметим, что выяснение достаточных условий геометрической неизменяемости невозможно вне структуры и характера закрепления стержневой системы. По этой причине не удается выделить достаточный признак в чистом виде: достаточные условия включают в себя неявно и необходимые условия геометрической неизменяемости.

Имея это в виду, остановимся на некоторых более употребительных формулировках достаточного признака геометрической неизменяемости, которые, по-видимому, из-за их процедурной конструктивности часто называют методами.

2.2.1. Аналитический метод. Этот общий метод сочетает в себе процедуру выяснения достаточных условий геометрической неизменяемости стержневой системы с процедурой нахождения внутренних сил в ее элементах.

Пусть ( ) — искомые внутренние (обобщенные) силы в элементах изучаемой стержневой системы, включая опорные стержни, и пусть процедура их определения сведена (см. последующие разделы) к решению системы линейных алгебраических уравнений

(2.3)

Если стержневая система статически определима, то коэффициенты зависят лишь от геометрии системы, а — и от параметров внешней нагрузки. В случае статически неопределимых систем эти величины будут зависеть также от упругих свойств элементов стержневой системы.

Согласно правилу Крамера решение системы (2.3) имеет вид

(2.4)

Здесь

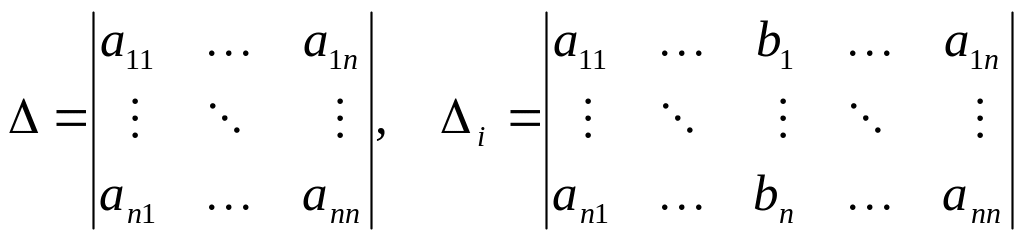
где — определитель системы, а — определитель, получаемый из путем замены его го столбца столбцом свободных членов системы (2.3).

Единственное и определенное решение (2.4) системы (2.3), возможное формально при , имеет смысл лишь при соблюдении равновесия стержневой системы в широком смысле. А это, как отмечалось выше, и означает геометрическую неизменяемость. Следовательно,

для того чтобы стержневая система была геометрически неизменяемой, необходимо и достаточно, чтобы .

Этот признак позволяет исследовать: для свободных стержневых систем — внутреннюю геометрическую неизменяемость, а для закрепленных систем — геометрическую неизменяемость в широком смысле.

2.2.2. Метод нулевых нагрузок. Этот метод вытекает из предыдущего при условии, что на стержневую систему не действуют внешние силы. В таком случае ( ), так что при имеем ( ). Таким образом, метод нулевых нагрузок можно сформулировать так:

для того чтобы стержневая система была геометрически неизменяема, необходимо и достаточно, чтобы при отсутствии внешних воздействий внутренние силы во всех без исключения элементах системы были равны нулю.

Любая неопределенность значения хотя бы одной внутренней силы свидетельствует о геометрической изменяемости системы.

2.2.3. Метод построения. Этот метод широко применяется проектантами. Идея его чрезвычайно проста и состоит в образовании стержневой системы путем должного синтеза заведомо геометрически неизменяемых стержневых подсистем (в частности, элементов стержневых систем). При этом необходимо соблюдать следующие правила:

1. Чтобы избежать внешней геометрической изменяемости, диск или плоскую стержневую систему следует прикреплять к опорам минимум тремя не сходящимися в одной точке (даже если она бесконечная) ферменными стержнями. Для блока или пространственной стержневой системы требуется минимум шесть таких стержней, при расположении которых необходимо позаботиться о том, чтобы у блока или системы не было центров и осей мгновенного вращения. По такому же принципу соединяются между собой, но уже в смысле отсутствия внутренней геометрической изменяемости, диски, блоки и, вообще, любые геометрически неизменяемые стержневые системы.

2. Чтобы избежать внутренней геометрической изменяемости, плоский ферменный узел следует присоединять к уже имеющейся стержневой системе минимум двумя неколлинеарными ферменными стержнями, а пространственный узел — тремя некомпланарными стержнями.

2.2.4. Метод разрушения. Этот метод обратный методу построения и заключается в последовательном отсоединении от исследуемой стержневой системы заведомо внутренне геометрически неизменяемых фрагментов (в частности, элементов стержневой системы), которые были прикреплены к соседним частям системы в согласии с правилами метода построения. Если в завершении этого процесса удается получить геометрически неизменяемый остаток стержневой системы, то можно утверждать, что исходная система также геометрически неизменяема.