1.8. Плоская задача теории упругости в полярных координатах

При решении краевых задач математической физики выбор тех или иных координат диктуется, прежде всего, формой границы области, в которой сформулирована краевая задача. Так в предыдущем параграфе при решении задач для прямоугольных областей использовались прямоугольные декартовые координаты. Полярную систему координат целесообразно применять в тех случаях, когда граница тела совпадает с ее координатными линиями (круглые и кольцевые пластины, пластины в форме кругового или кольцевого сектора и т. п.). Во всех таких случаях использование полярных координат приводит к значительному упрощению решения задачи.

1.8.1. Основные уравнения плоской задачи в полярных координатах. В полярных координатах положение точки тела определяется координатами и , связанными с декартовыми координатами и этой же точки уравнениями

Вывод основных уравнений начнем со статических соотношений.

В ыделим из тела бесконечно малый объем, заключенный между координатными линиями , , , (см. рис. 1.10).

С точностью до линейных приращений на этот элемент действуют следующие напряжения: на грани и , — соответственно и , , а на грани и — соответственно и , . По аналогии с декартовыми координатами через и мы обозначили нормальные напряжения на площадках, нормали к которым ориентированы вдоль координатных линий и а через , ( ) — касательное напряжение.

Принятое для них правило знаков показано на том же рисунке. Помимо напряжений на выделенный элемент действуют объемные силы, интенсивности проекций которых на координатные линии и мы обозначим через и соответственно.

Составим уравнения равновесия элемента объема путем проектирования действующих на него сил на оси r и , полагая, что толщина рассматриваемой пластины равна 1, а в силу малости угла

Тогда найдем

Приводя подобные члены и отбрасывая бесконечно малые величины третьего порядка малости, разделим оба уравнения на и перейдем к пределу, когда элемент объема подобным образом стягивается в точку . Тогда приходим к следующим уравнениям локального равновесия в полярных координатах

(1.70)

Мы приняли, что . Доказать этот закон парности касательных напряжений можно путем рассмотрения равновесия элемента объема в отношении моментов вокруг оси . Но мы на этом не останавливаемся.

В декартовых координатах уравнения равновесия при отсутствии объемных сил были удовлетворены введением функции напряжений. Аналогичный результат имеет место и в полярных координатах. Пусть — функция напряжений. Тогда легко убедиться, что выражения

(1.71)

при обращают уравнения (1.70) в тождества типа .

Обратимся теперь к геометрическим соотношениям. Условимся перемещения точки вдоль осей и обозначать символами и , а деформации удлинения вдоль осей , и деформацию сдвига (уменьшение прямого угла между осями и — символами , и соответственно.

Выразим деформации через перемещения. С этой целью рассмотрим деформированное состояние бесконечно малого элемента, показанное на рис.1.11. С точностью до линейных приращений можно записать

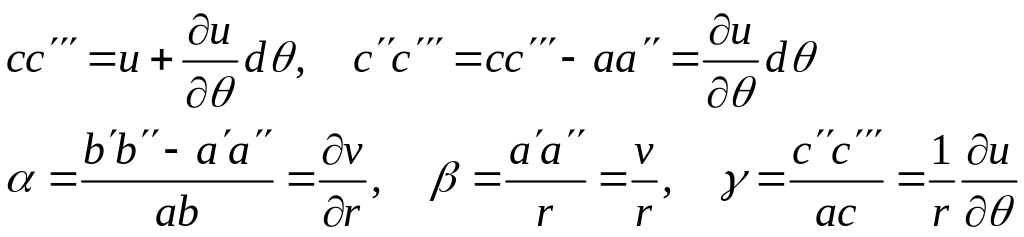
С учетом этих выражений по определению деформаций находим

(1.72)

Путем исключения из этих уравнений перемещений можно найти условие сплошности

(1.73)

З акон Гука (1.61) сохраняет свой прежний вид и меняются лишь обозначения напряжении и деформаций.

(1.74)

При решении плоской задачи в напряжениях помимо уравнений равновесия (1.70) следует привлечь условие сплошности (1.73), выраженное через напряжения. Подставляя (1.74) в (1.73) и преобразовывая их с помощью уравнений равновесия, получим

(1.75)

где

(1.76)

— дифференциальный оператор Лапласа в полярных координатах.

С учетом (1.71) уравнение Морриса Леви (1.75) примет вид

(1.77)

Это и есть разрешающее уравнение метода напряжений в полярных координатах. Это, по существу, — переписанное в полярных координатах уравнение (1.68).