1.5. Обобщенный закон Гука

Рассмотренные в двух предыдущих параграфах теория напряжений и теория деформаций позволяют охарактеризовать статическую и геометрическую стороны процесса деформирования любой сплошной среды. При малых перемещениях и деформациях эти две теории не связаны между собой и потому не могут быть использованы для решения физических задач теории упругости до тех пор, пока не будет установлена зависимость между напряжениями и деформациями. Эта зависимость является математическим выражением физического закона процесса деформирования, призванного связать разнородные признаки изучаемого явления — статику и кинематику.

Ближайшая наша цель — изучение физической стороны процесса деформирования линейно-упругих тел, основное содержание которой составляет зависимость между напряжениями и деформациями в форме обобщенного закона Гука.

Общая связь между напряжениями и деформациями в упругих телах. Упругие тела после устранения внешних воздействий возвращаются в исходное (недеформированное) состояние; иначе — процесс деформирования упругих тел всегда обратим.

Аналитически это можно выразить общими зависимостями вида

(1.22)

которые в каждой точке рассматриваемого деформируемого тела устанавливают взаимно-однозначное соответствие между напряжениями и деформациями и, следовательно, однозначно разрешимы относительно последних

Согласно гипотезе о естественном состоянии тела все функции , ( ) обращаются в нуль при нулевых значениях их аргументов.

При малых деформациях выражения 1.22 можно заменить их линейными аппроксимациями

(1.23)

получаемыми путем разложения в ряд Тэйлора соответствующих функций в окрестности недеформированного состояния с последующим удержанием линейных членов. Смысл величин ( ) вытекает из описанной процедуры. Например,

где значок “0” указывает на то, что значение частной производной берется в недеформированном состоянии, когда все деформации обращаются в нуль.

Величины характеризуют упругие свойства тела и носят название упругих постоянных. Слово "постоянные" здесь следует понимать в том смысле, что названные ими величины не зависят от деформаций и напряжений, но могут, вообще говоря, зависеть от пространственных координат.

Линейные зависимости (1.23) носят название обобщенного закона Гука (в отличии от закона Гука в теории растяжения–сжатия стержней или в теории чистого сдвига). По своему существу они формулируют закон независимости действия (принцип суперпозиции) для напряжений, предполагающий, что, например, напряжение , возникающее при наличии нескольких деформаций, равно сумме напряжений, возникающих от каждой деформации в отдельности.

По упругим свойствам деформируемые тела можно разделить неоднородные и однородные, изотропные и анизотропные. В однородных телах упругие свойства не зависят от рассматриваемой точки. Математически это выражается в том, что упругие постоянные не зависят от координат. Тело называется изотропным, если его упругие свойства в каждой точке не зависят от направления (рассматриваемой системы координат). Однородное или неоднородное тело может быть, в свою очередь, изотропным или анизотропным.

В природе нет идеально однородных и изотропных тел, но есть много важных с технической точки зрения материалов, которые в известном приближении можно считать однородными и изотропными. Так, например, металлы состоят из различных неизотропных частиц (кристалликов), беспорядочно расположенных друг относительно друга. Эта хаотичность в строении приводит к тому, что эти материалы ведут себя в среднем (в статистическом смысле) как однородные и изотропные.

Следует еще заметить, что тело, изотропное и однородное относительно одних свойств, может быть анизотропным и неоднородным в отношении других. В дальнейшем ограничимся рассмотрением, главным образом, изотропных и однородных тел, понимая под этим однородность и изотропность в смысле упругих свойств. Математически это выразится в том, что коэффициенты в формулах (1.23) не будут зависеть от ориентации осей координат и положения рассматриваемой точки в теле.

Установлению обобщенного закона Гука предпошлем некоторые вспомогательные результаты.

1.5.1. Потенциал напряжений. Ограничиваясь рассмотрением процессов деформирования без тепловых эффектов, примем деформации за независимые параметры состояния деформируемого тела. Тогда потенциальная энергия деформированного тела

Для краткости будем писать

Отсюда находим

(1.24)

Эти формулы носят название формул Грина и показывают, что потенциалом напряжений является плотность потенциальной энергии деформации.

В случае линейно-упругого тела согласно (1.23) все частные производные от являются линейными и однородными многочленами первой степени относительно деформаций. Отсюда можно сделать заключение: есть однородный многочлен второй степени относительно тех же величин, то есть, если — некоторый числовой параметр, то

(1.25)

или с учетом формул Грина

(1.26)

Полученное соотношение носит название формулы Клапейрона.

1.5.2. Потенциал деформаций. В рамках допущений предыдущего пункта примем теперь действующие в теле напряжения за независимые параметры состояния деформируемого тела. Имеем

и далее

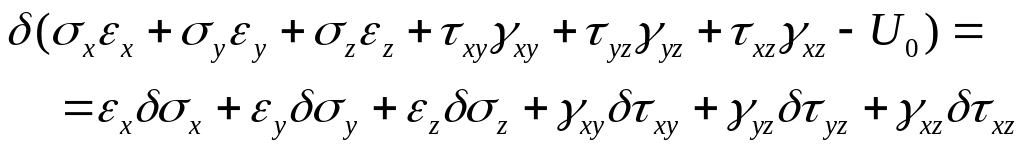(1.27)

Это выражение показывает, что функция

, (1.28)

называемая плотностью дополнительной потенциальной энергии деформации, является полным дифференциалом своих аргументов, причем

(1.29)

Эти соотношения известны под названием формул Кастильяно. Они показывают, что дополнительная потенциальная энергия единицы объема является потенциалом деформаций.

Если тело линейно-упругое, то из формулы Клапейрона и выражения (1.29) следует

(1.30)

и формулы Кастильяно приобретают вид

(1.31)

1.5.3. Обобщенный закон Гука для однородного изотропного тела. В уравнения обобщенного закона Гука (1.23) входит, вообще говоря, 36 упругих констант. Для однородного тела они не зависят от координат , , . Из существования потенциала напряжений (см. (1.22), (1.23)) и независимости значения второй производной функции от порядка дифференцирования следует, что упругие постоянные, расположенные симметрично относительно главной диагонали, попарно равны между собой.

Таким образом, число упругих постоянных сокращается до 21.

Воспользуемся теперь свойством изотропии материала — независимостью его упругих свойств от выбранной системы координат — и покажем, что число независимых упругих постоянных равно двум:

(1.32)

Напомним, что — объемная деформация,

(1.33)

Нетрудно показать, что обратная форма обобщенного закона Гука имеет вид

(1.34)

Физически очевидно, что и всегда имеют одинаковый знак (при всестороннем сжатии, например, не может увеличиваться объем). Поэтому и, следовательно, . Для большинства металлов .

1.5.4. Температурные напряжения. Раздел теории упругости, изучающий процессы деформирования нагретых упругих тел, называется термоупругостью. В общей постановке задачи термоупругости — связанные и должны решаться с учетом тепловых явлений, как в самом теле, так и во взаимодействии его с окружающей средой. Мы ограничимся рассмотрением несвязанной термоупругости, предполагающей присутствие в теле заданного поля температур, обеспечиваемого необходимыми процессами в окружающей среде (теплоотдачей) и в теле (теплопроводностью) При таких предположениях температура может выступать лишь как параметр состояния деформируемого тела.

Пусть — изменение температуры тела в точке в момент времени отсчитываемое от некоторой начальной, постоянной для всего тела, температуры . В соответствии со сказанным выше удовлетворяет уравнению теплопроводности, начальным и граничным условиям. Рассмотрим малый объем тела в форме с ребрами, параллельными выбранным осям координат. В пределах объема этого параллелепипеда температуру можно считать постоянной. Пусть — коэффициент линейного температурного расширения, одинаковый во всех направлениях (тело изотропное). Если бы параллелепипед был свободен, то за счет нагрева до температуры он превратился бы в новый параллелепипед, размеры которого вдоль осей увеличились за счет деформаций удлинения одинаковых по всем направлениям. Деформации бы сдвига при этом отсутствовали.

Однако свободному расширению параллелепипеда препятствуют окружающие его части тела, что вызывает появление упругих деформаций.

В основу несвязанной термоупругости положена гипотеза Дюгамеля-Неймана, состоящая в том, что напряжения в термоупругом теле связаны с упругими деформациями обычными соотношениями обобщенного закона Гука, а полные деформации (сумма упругих и температурных) выражаются через компоненты упругого смещения обычными соотношениями Коши. На основании этой гипотезы можно записать (см. (1.17), (1.34))

(1.35)

Если разрешить эту систему относительно напряжений, то получим

(1.36)

Таким образом, в термоупругой несвязанной задаче учет температурного воздействия формально сводится к замене обычных уравнений обобщенного закона Гука (1.37). (1.34) зависимостями (1.35). (1.36) соответственно.