4. Еквівалентність відсоткових ставок.

Принцип еквівалентності у фінансових операціях означає, що при змінах в угодах та контрактах, фінансові зобов’язання залишаються незмінними. Цей принцип підтримує довіру партнерів та беззбитковість сторін при змінах в контрактах. Еквівалентними називають різні за видом та схемами обчислення відсоткові ставки, які в однотипних фінансових операціях дають однакові кінцеві результати. [4]

Еквівалентність декурсивних і облікових ставок відсотків.

Знайдемо еквівалентні ставки для облікової та декурсивної ставки відсотків. Формули кінцевої суми боргу для обох ставок еквівалентні, а тому прирівнюються.

1. Прості відсотки:

=

Якщо ліві частини формул рівні, тоді їх праві частини теж рівні. З даних формул можемо виразити просту облікову ставку через просту декурсивну і навпаки:

; .

2)Складні відсотки:

=

Якщо ліві частини формул рівні, тоді їх праві частини теж рівні. З даних формул можемо виразити складну облікову ставку через складну декурсивну і навпаки: ; .

Приклад 10.

За формулами еквівалентності декурсивної та облікової ставок визначити облікову просту і складну ставки на основі заданої декурсивної ставки 4% за умови, що строк позики дорівнює 20 місяців при щомісячному нарахуванні.

Розв’язок:

Облікова ставка на основі декурсивної ставки дорівнює:

а) проста: або 2.22%

б) складна: або 3.85%

Відповідь: проста облікова ставка становить 2.22%, складна облікова ставка становить 3.85%.

Еквівалентність простих і складних ставок відсотків.

Розглянемо співвідношення простих і складних ставок відсотків, що дає змогу беззбитково замінювати їх при зміні умов контрактів.

Д ля декурсивних ставок позначимо через і_п – просту ставку відсотків, через і_с – складну ставку. З формул простих і складних відсотків зазначимо умову еквівалентності:

;

=

Із системи рівнянь виразимо складну ставку через просту і навпаки:

; .

Аналогічно можна виразити просту облікову ставку через складну облікову і навпаки.

Приклад 11.

Кредит надано під 24% складних річних. Якою повинна бути еквівалентна ставка простих відсотків, якщо термін кредиту а) 2 роки; б) півроку.

Розв’язання:

а)

б)

Відповідь: а) в першому випадку потрібна ставка простих відсотків більша ніж ставка складних відсотків для отримання того самого ефекту – 26.9%; б) в другому випадку менша за величиною ставка простих відсотків дає такий самий ефект, що і складна ставка відсотків – 22.7%.

Номінальна ставка і ставка ефективності.

Складні відсотки можуть нараховуватись частіше ніж раз на рік, але в угоді може бути зазначена річна ставка та період нарахування.

Наприклад: річна ставка відсотків – 24%, відсотки нараховуються щомісяця. Це означає, що кожен місяць буде нараховуватись 2%, а за рік щомісячні ставки складуть 24% ( 2% x 12 = 24% ).

Річна сумарна ставка відсотків називається номінальною ставкою. Капіталізація суми боргу за номінальною ставкою відсотків відбувається за формулою: , де і_Н – номінальна ставка відсотків, m – кількість нарахувань за рік; – ставка відсотків за якою реально будуть нараховуватись відсотки кожного періоду нарахування, - множник нарощення за номінальною ставкою. [2]

Приклад 12.

Фірма позичає в банку суму 100 тис. грн. на строк 2 роки. Нарахування відсотків щоквартальне, річна ставка складних відсотків 16%. Якою буде кінцева сума боргу?

Розв’язання:

Відповідь: кінцева сума боргу складе 136856.91 грн.

Якою буде річна ставка, яка при нарахуванні раз на рік буде давати такий самий ефект, що і номінальна? Ставка відсотків, яка є еквівалентною номінальній ставці при нарахуванні відсотків m раз на рік, називається ставкою ефективності. Ця ставка показує реальний відносний дохід, який отримують у цілому за рік. [4]

Знайдемо відповідність номінальної ставки ставці ефективності, використовуючи принцип еквівалентності:

, де і_Е – ставка ефективності.

=

Із системи рівнянь виразимо номінальну ставку та ставку ефективності:

; .

Приклад 13.

Банк нараховує за позику відсотки за номінальною ставкою 24%. Яка реальна дохідність фінансового зобов’язання, якщо відсотки нараховуються а) щомісяця; б) щокварталу; в) що півроку.?

Розв’язання:

а)

б)

в)

Відповідь: реальна дохідність фінансового зобов’язання тим вища, чим частіше нараховуються відсотки: а) 26.8%; б) 26.2%; в) 25.4%.

Середня відсоткова ставка.

Якщо під час дії угоди відсоткові ставки змінюються, можлива заміна цих ставок однією еквівалентною, яка буде приносити за період такий самий дохід. Ця ставка називається середньою.

Позначимо:

• через n₁; n₂;…; n_k – періоди нарахування,

• через i₁; i₂;…; i_k – декурсивні відсоткові ставки.

Тоді загальний строк нарахування становить:

,

де n_t – t-тий період нарахування.

Середня декурсивна відсоткова ставка ( ) обчислюється за формулою середньої арифметичної:

.

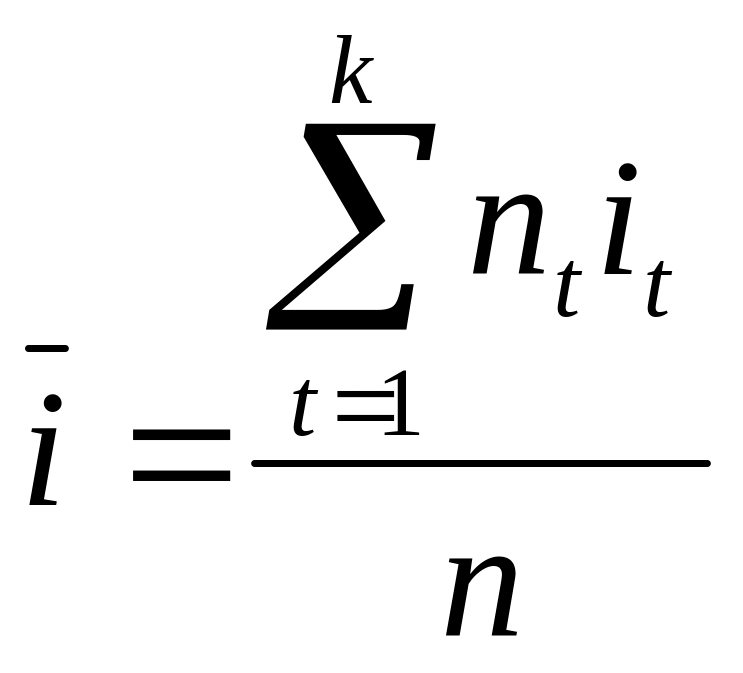Аналогічно розраховується середня облікова ставка.