Задачи для самостоятельного решения
Вычислить следующие интегралы.
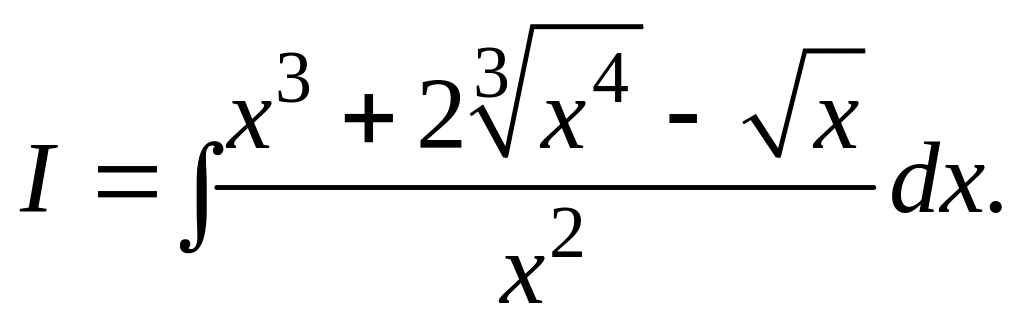1.8.
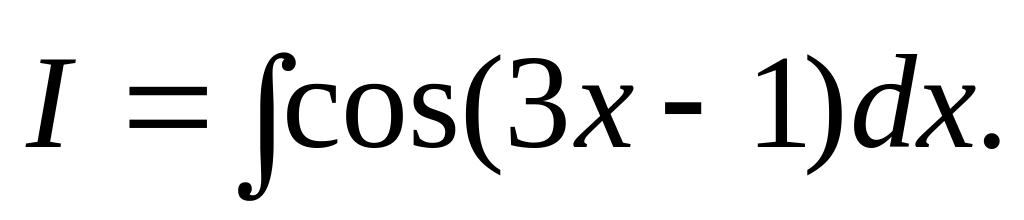
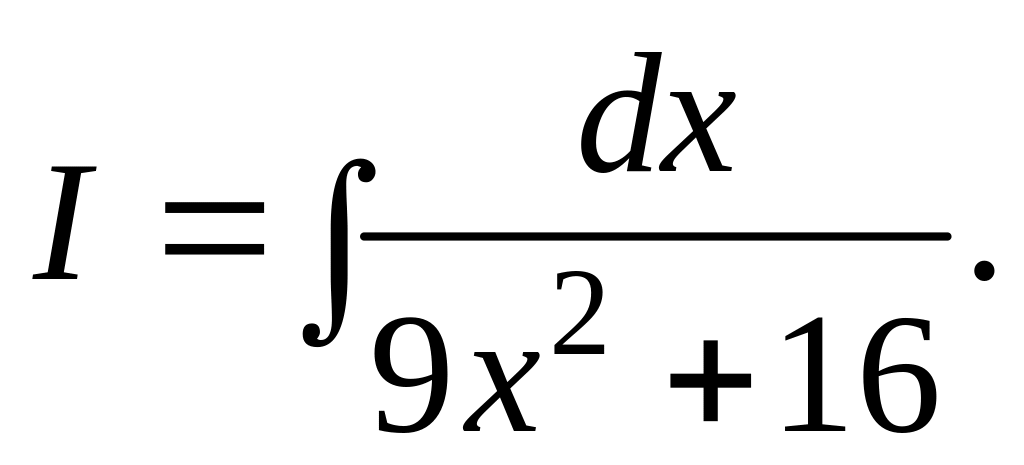1.10.
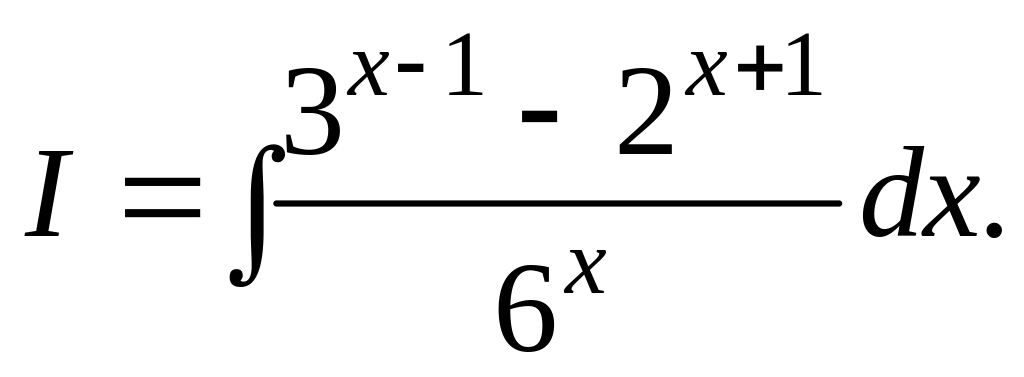
1.11.
I
=
1.12.
I
=
1.13.
§ 2. Замена переменной в неопределенном интеграле
Часто при вычислении НИ очень полезным оказывается переход к новой переменной или, как иногда говорят, метод подстановки. Пусть функция x = φ(t) определена и дифференцируема на некотором интервале (ά, β) и пусть Х – множество значений этой функции – интервал, полуинтервал или отрезок. Пусть на Х определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на интервале (α, β) справедлива формула замены переменной в НИ:
Рассмотрим пример.
Решение. Сделаем в интеграле замену переменной x – 3 = t и вычислим интеграл
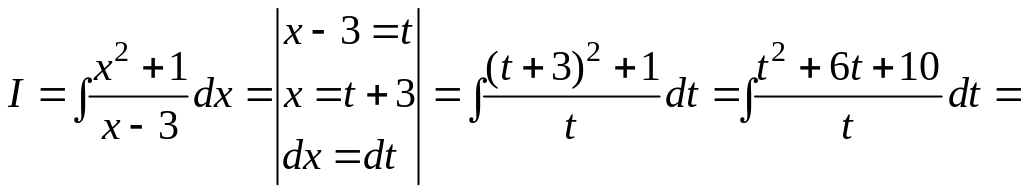
В приведенных выкладках вертикальными черточками отделены вспомогательные рассуждения. Это позволяет не прерывать цепочку выкладок. Далее такая форма записи вычислений будет использоваться систематически.
Рассмотрим несколько примеров.
.
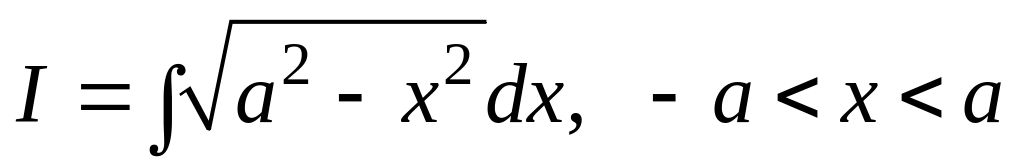Решение. Делая тригонометрическую подстановку, вычисляем интеграл
=
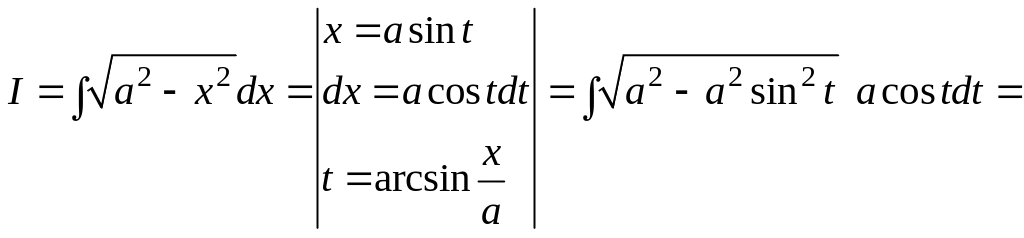
2.3.
Решение. Делая замену переменной, вычисляем
.
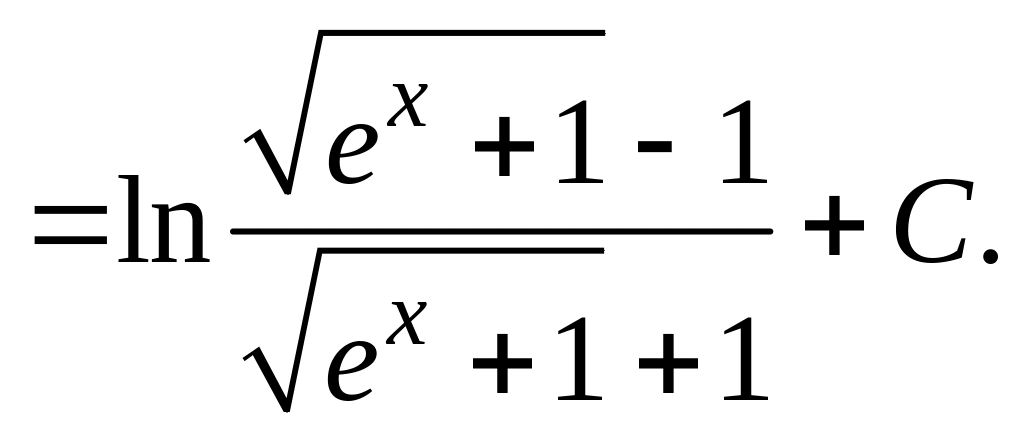
Решение. Будем считать, что x > a > 0. Как правило, неопределенный интеграл можно вычислить несколькими способами. Вычислим интеграл этого примера двумя способами.
А. Домножим числитель и знаменатель подынтегральной дроби на x и сделаем замену переменной. Получим
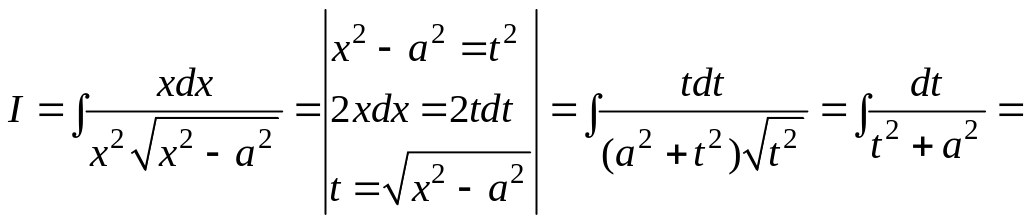
Б.
Вынесем
из-под корня и сделаем замену переменной
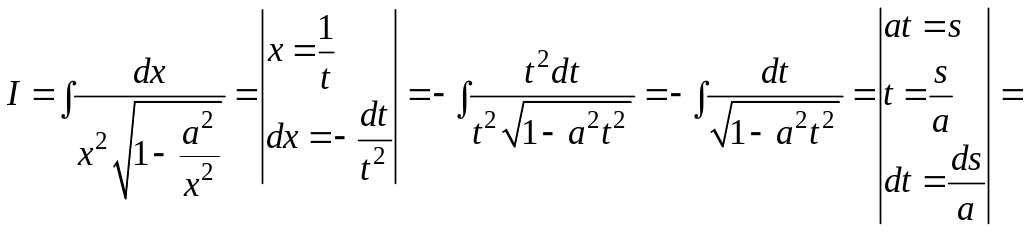
Вид
получившейся первообразной отличен от
вида первообразной, полученной в случае
А. Но если обозначить arccos
то
.
Тогда
Следовательно, в обоих случаях первообразной является одна функция.
.
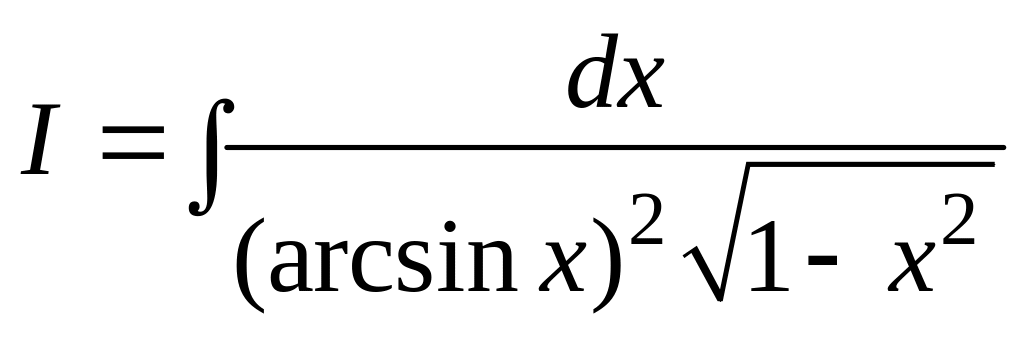Решение. Делая замену переменной, вычисляем
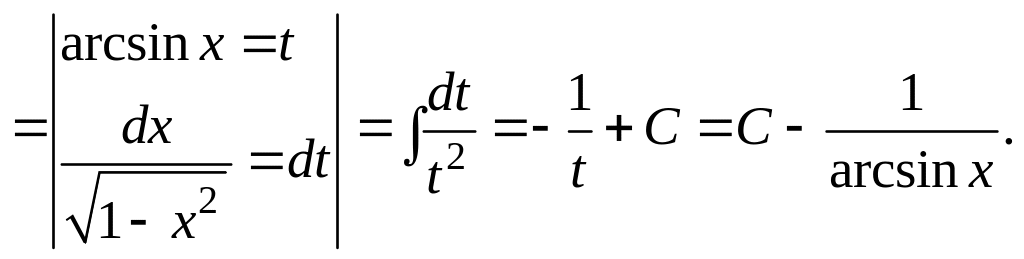
Отметим некоторые типичные случаи применения замены переменной. Рассмотрим сначала следующий интеграл:
после
замены
.
В частности, при a
= 2 имеем
Рассмотрим пример, который понадобится нам в дальнейшем.
2.6.
.
Решение.
В этом примере
.
Делая замену переменной, получаем
,
Часто встречаются также следующие подстановки:
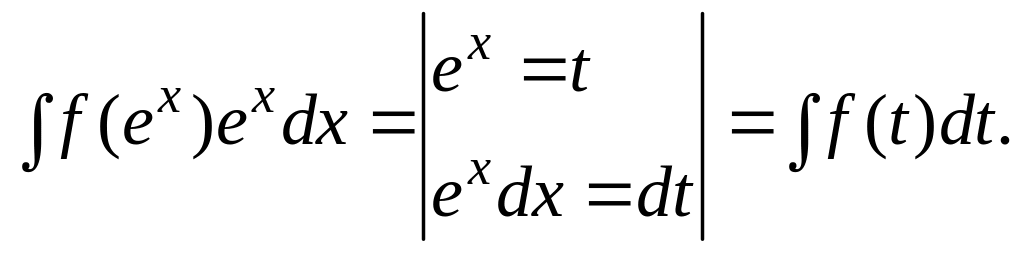
Задачи для самостоятельного решения
Вычислить интегралы.
2.9.
2.10.
2.11.
2.12.
2.13.
§ 3. Интегрирование по частям
Пусть u и v – дифференцируемые функции. Формулой интегрирования по частям называется формула
Поскольку
,
то формулу интегрирования по частям
можно записать в более простом виде
Интегрирование
по частям чаще всего применяется тогда,
когда производная
является «более простой», чем сама
функция u.
При этом, естественно, функция v
должна относительно просто находиться
по заданному дифференциалу
.
Рассмотрим примеры.
Решение. За функцию u в этом примере естественно принять u = = x – 1, так как du = dx. Вычисляем интеграл.
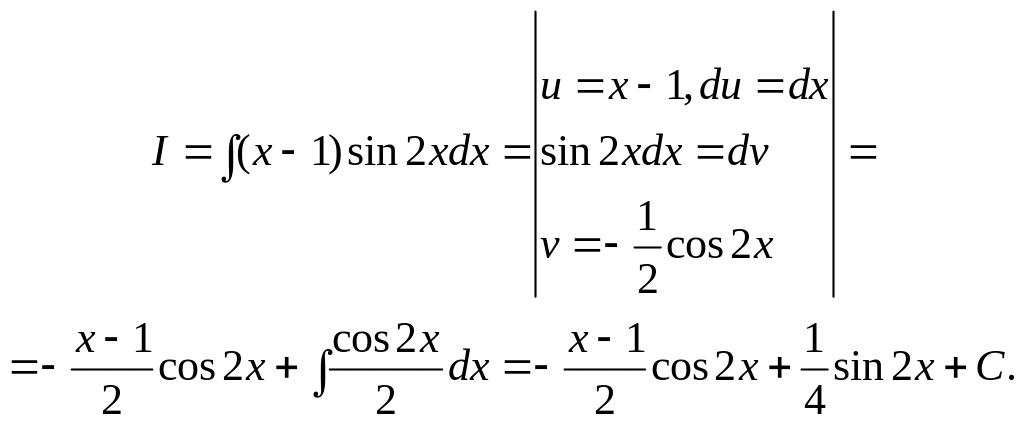
Решение. Здесь мы однозначно решаем, что u = arctg x. Применяя формулу интегрирования по частям, вычисляем
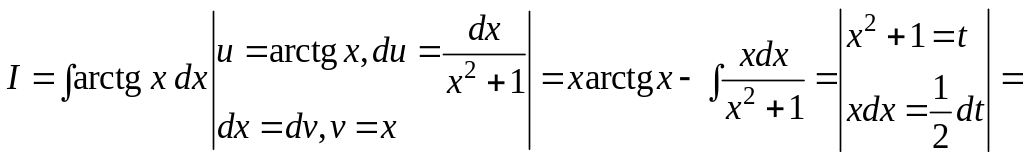
Интегрированием по частям можно вычислить интегралы:
,
где
многочлен, и многие другие. Действительно,
рассмотрим, например, интеграл
Если положить u
= P(x),
,
то согласно формуле интегрирования по
частям получаем
Мы
получаем интеграл того же вида, что и
первоначальный, но теперь многочлен
имеет степень меньшую, чем у многочлена
.
Далее можно снова применить формулу
интегрирования по частям, затем еще раз
и далее, пока не придем к табличному
интегралу
К интегралам вида
сводятся интегралы вида
Действительно, после замены переменной
,
получаем
.
В интегралах, содержащих обратную тригонометрическую функцию, за функцию u следует брать эту функцию.
Рассмотрим примеры.
3.3.
Решение. Положим u = arctg x, x dx = dv. Тогда
Применяя формулу интегрирования по частям, вычисляем
3.4.
Решение.
В этом примере
Берем интеграл по
частям:
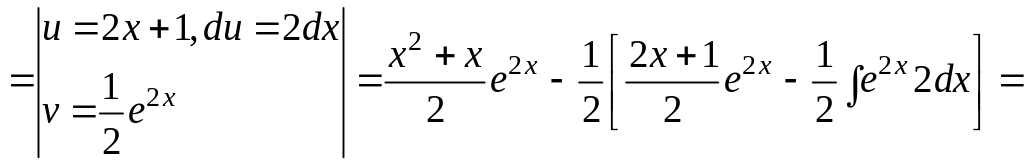
3.5.
Решение. Сначала преобразуем подынтегральную функцию, затем сделаем замену переменной:
.
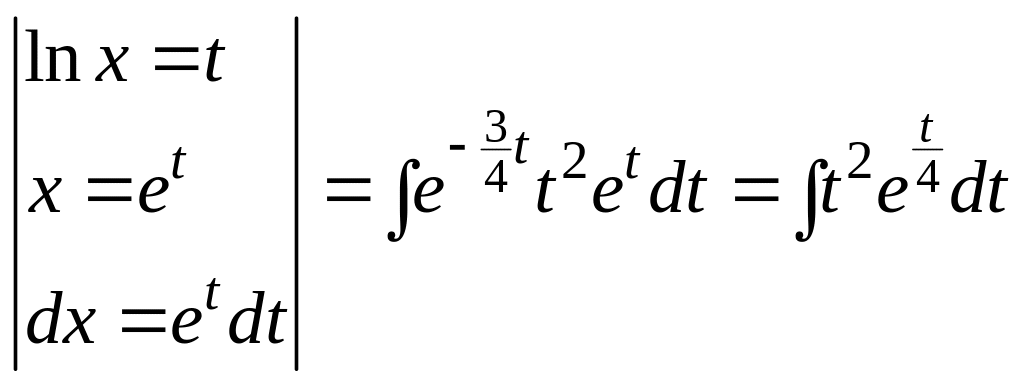Теперь применяем формулу интегрирования по частям:
3.6.
Решение. Этот интеграл можно вычислить разными способами. Можно, например, сделать тригонометрическую подстановку x = a tg t или гиперболическую (гиперболические функции мы рассмотрим дальше) x = a sh t. Мы возьмем этот интеграл по частям. Сначала преобразуем подынтегральную функцию:
Обозначим
интеграл в правой части через
и вычислим его интегрированием по
частям:
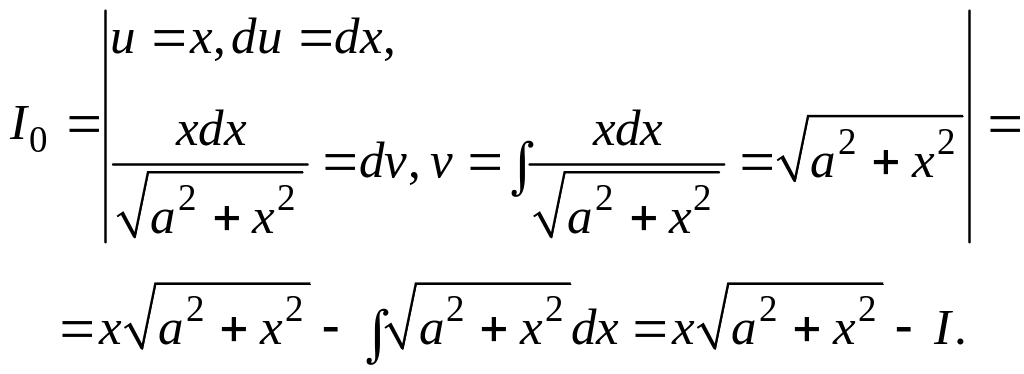
Таким образом,
.
Решая
это уравнение относительно
,
находим
3.7.
Решение. Мы вычислим этот интеграл с помощью повторного применения формулы интегрирования по частям, получив простое уравнение для нахождения исходного интеграла:
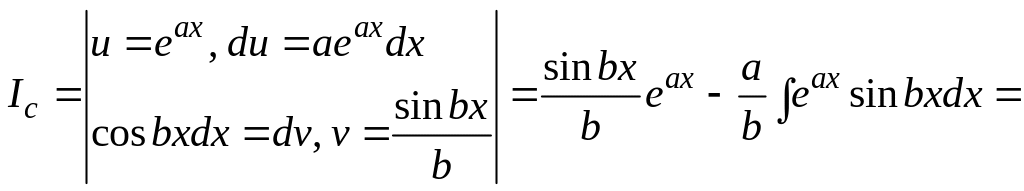
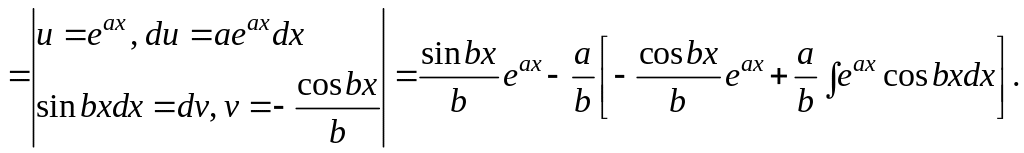
Таким образом, мы приходим к уравнению
.
Решая
это уравнение относительно
,
находим
3.8. Аналогично вычисляется интеграл
.
К
интегралам
и
приводятся после замены переменной
интегралы
и
Действительно, сделав замену переменной
ln
x
= t,
получим
3.9.
Аналогично вычисляется интеграл
Используя
интегралы из примеров 3.7 и 3.8 и формулу
интегрирования по частям, можно вычислять
интегралы вида
и
.
Решение. Используя интегралы из примеров 3.7 и 3.8 и формулу интегрирования по частям, вычисляем наш интеграл
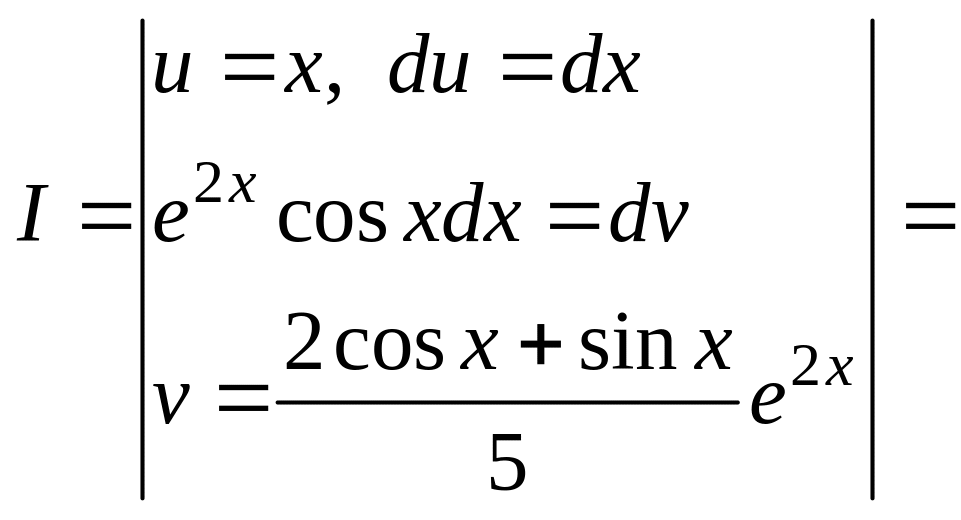
Одним из применений метода интегрирования по частям является вывод рекуррентных формул. В этих формулах интегралы, зависящие от индекса n > 0 (n N), выражаются через интегралы того же типа с меньшими индексами.
Рассмотрим несколько примеров.
Решение. Сначала преобразуем подынтегральную функцию:
Интеграл в правой части преобразуем с помощью формулы интегрирования по частям:
Для нахождения функции v мы воспользовались примером 2.6. Таким образом, мы получаем
.
Отсюда следует рекуррентная формула
Так как при n = 1
то при n = 2 получаем
При n = 3 имеем
и т. д.
Используя метод интегрирования по частям, можно получить следующие рекуррентные формулы:
.
.
.
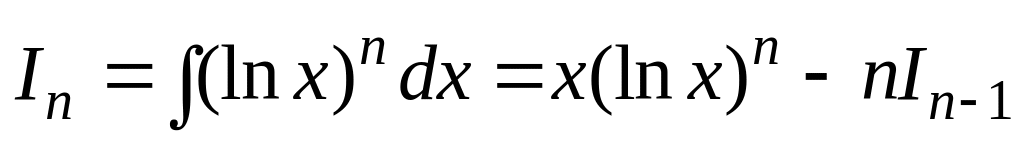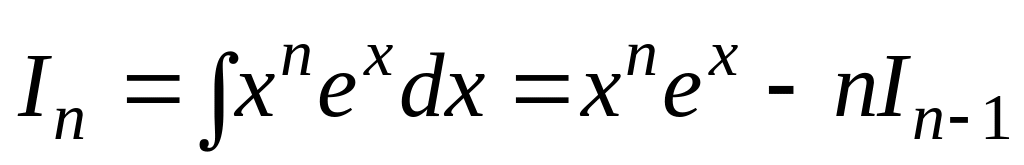Покажем, как выводится формула из примера 3.13. Вывод формул из примеров 3.14 и 3.15 оставляем читателям.
Решение.
Применяем формулу интегрирования по
частям, полагая
dx
= dv.
Тогда
и 
.
Рассмотрим еще один пример.
Решение. Применим сначала формулу интегрирования по частям, а затем произведем несложные преобразования подынтегральной функции:
Приведя подобные члены, отсюда получаем
(2β
+ 1)I
I
Например, так как
то
и т.д.
Интегрированием
по частям выводятся рекуррентные формулы
для интегралов
и многие другие.
При вычислении некоторых интегралов приходится применять формулу интегрирования по частям несколько раз. В таких случаях часто удобнее применять обобщенную формулу интегрирования по частям:
где
Особенно удобна формула, когда u = P(x) – многочлен степени n.
Решение.
Пусть
Тогда
Вычисляем далее
Применяя теперь обобщенную формулу интегрирования по частям, находим интеграл
