
- •Решение задач по теме «интегральное исчисление функций одной переменной»
- •Предисловие
- •Глава 1 неопределенные интегралы
- •§ 1. Непосредственное интегрирование
- •Задачи для самостоятельного решения
- •§ 2. Замена переменной в неопределенном интеграле
- •Задачи для самостоятельного решения
- •§ 3. Интегрирование по частям
- •Задачи для самостоятельного решения
- •§ 4. Интегралы и
- •Задачи для самостоятельного решения
- •§ 5. Интегрирование рациональных функций
- •Задачи для самостоятельного решения
- •§ 6. Интегрирование иррациональных функций
- •Задачи для самостоятельного решения
- •§ 7. Интегрирование тригонометрических функций
- •Задачи для самостоятельного решения
- •§ 8. Гиперболические функции. Тригонометрические и гиперболические подстановки
- •Задачи для самостоятельного решения
- •Ответы и указания
Глава 1 неопределенные интегралы
§ 1. Непосредственное интегрирование
Пусть
на интервале (a,
b)
определена некоторая функция f(x).
Тогда функция F(x),
определенная так же на (a,
b),
называется первообразной функции f(x),
если F(x)
= f(x)
для x
![]() (a,
b).
Например, функция F(x)
= = sin 3x –
первообразная функции f(x)
= 3 cos 3x,
а F(x)
= x3
+3 –
первообразная f(x)
= 3x2.
Известно, что все первообразные одной
функции отличаются друг от друга на
постоянное слагаемое. Отсюда следует,
что если F(x)
– некоторая первообразная функции
f(x),
то любая другая первообразная Φ(x)
имеет вид Φ(х)
= F(x)
+ C,
где C
– постоянная, зависящая только от Φ.
(a,
b).
Например, функция F(x)
= = sin 3x –
первообразная функции f(x)
= 3 cos 3x,
а F(x)
= x3
+3 –
первообразная f(x)
= 3x2.
Известно, что все первообразные одной
функции отличаются друг от друга на
постоянное слагаемое. Отсюда следует,
что если F(x)
– некоторая первообразная функции
f(x),
то любая другая первообразная Φ(x)
имеет вид Φ(х)
= F(x)
+ C,
где C
– постоянная, зависящая только от Φ.
Неопределенным
интегралом (НИ) от функции f(x)
называется множество всех первообразных
функции f.
Обозначается НИ от f
следующим образом:
![]() .
Таким образом,
.
Таким образом,
![]() .
.
Обычно, следуя традиции, пишут просто
![]() .
.
Переменная x называется переменной интегрирования, f(x) называется подынтегральной функцией, f(x) dx – подынтегральным выражением. Процесс нахождения неопределенного интеграла от функции f(x) называется интегрированием функции f. Принято говорить также: «Взять интеграл ».
Вычисление
НИ есть в определенном смысле операция,
обратная к нахождению дифференциала
функции. Действительно, пусть F(x)
–первообразная функции f(x).
Тогда
![]() = d(F(x)
+ C)
= F’(x)dx
= = f(x)dx.
С другой стороны,
= d(F(x)
+ C)
= F’(x)dx
= = f(x)dx.
С другой стороны,
![]() =
=
![]() =
= F(x)
+ C.
=
= F(x)
+ C.
Отсюда вытекает, что из таблицы производных основных элементарных функций можно получить таблицу интегралов от основных элементарных функций. Эти интегралы называются табличными. Приведем здесь таблицу этих интегралов.
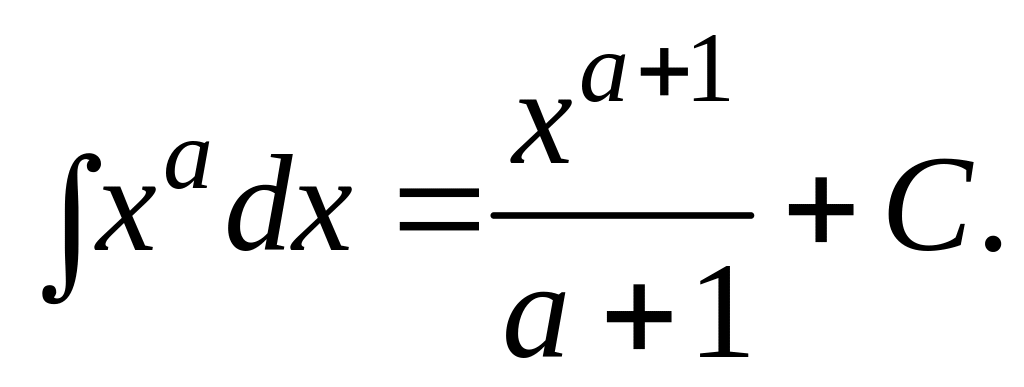
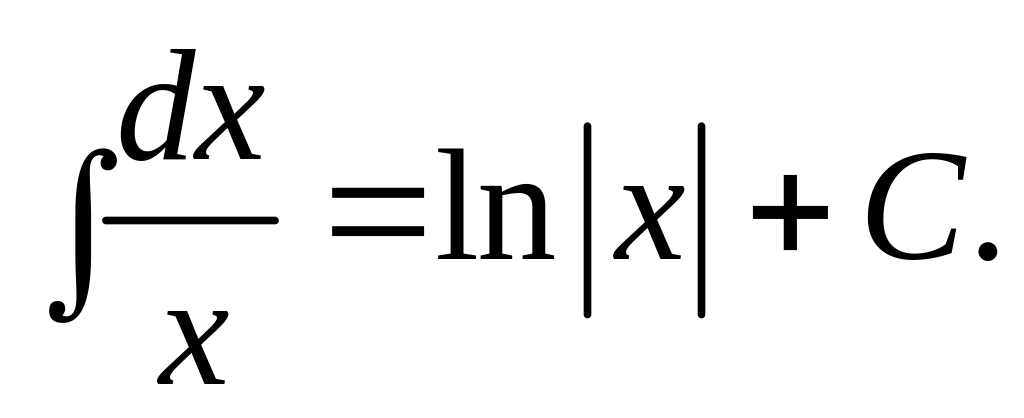
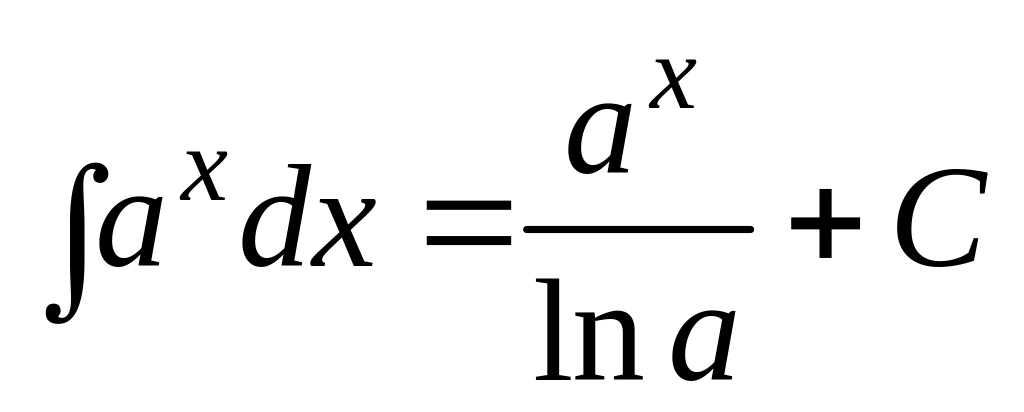 ,
,
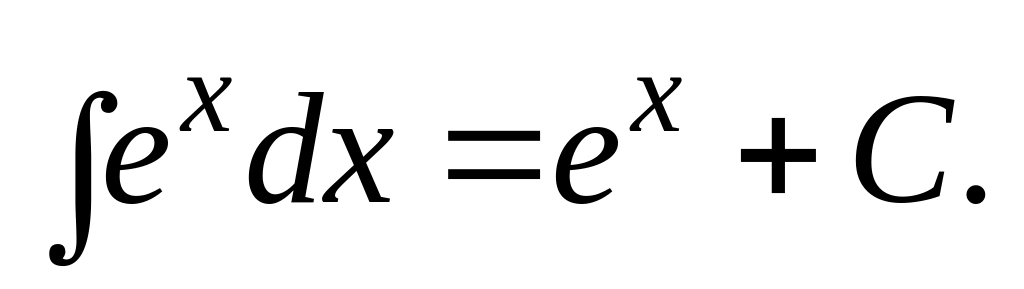
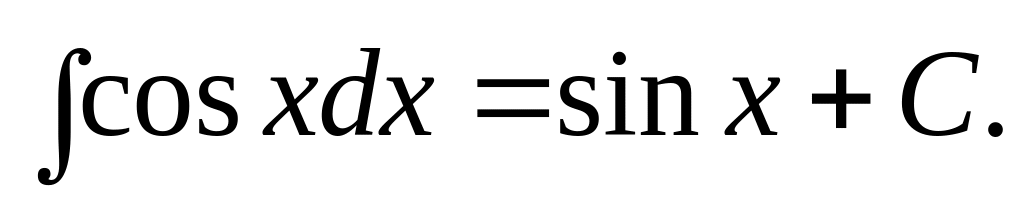

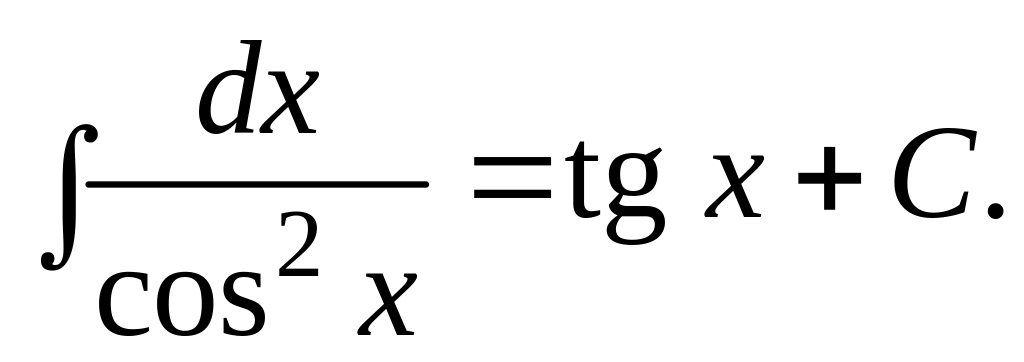
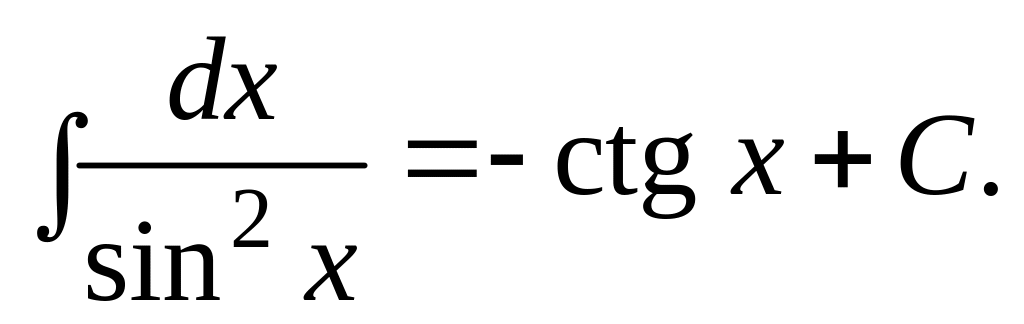
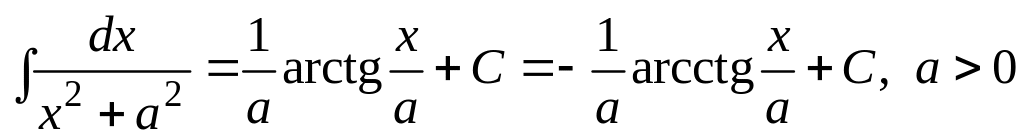 .
.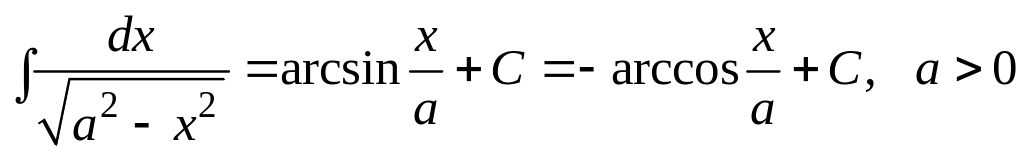 .
.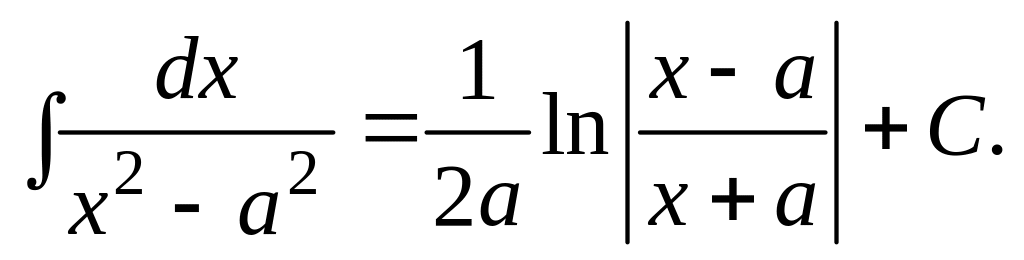
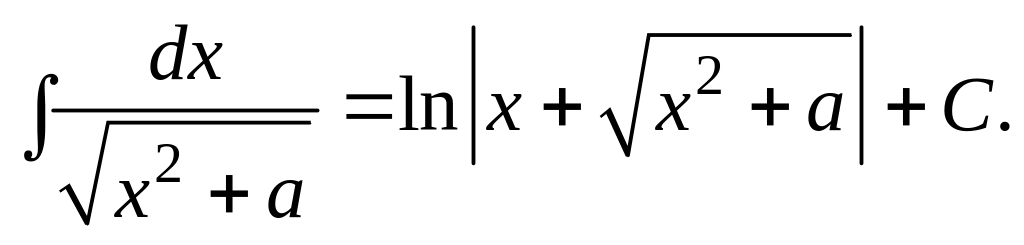
Вычисление
НИ в основном заключается в сведении
его к табличному интегралу. Достигается
это с помощью свойства линейности НИ,
а также с помощью некоторых приемов, о
которых речь будет ниже. Необходимо
отметить, что в то время как, используя
правила дифференцирования, можно
вычислить производную любой элементарной
функции, и эта производная снова будет
элементарной функцией, неопределенный
интеграл от элементарной функции может
оказаться неэлементарной функцией. В
этом случае говорят, что интеграл «не
берется» и называют его «неберущимся».
Таковы, например, интегралы
![]()
![]()
![]() и др. В связи с этим становится очевидным,
что необходимо хорошо знать основные
классы функций, для которых НИ являются
элементарными функциями («берущиеся»
интегралы), и, решая примеры, хорошо
освоить основные методы интегрирования.
и др. В связи с этим становится очевидным,
что необходимо хорошо знать основные
классы функций, для которых НИ являются
элементарными функциями («берущиеся»
интегралы), и, решая примеры, хорошо
освоить основные методы интегрирования.
Напомним свойство линейности НИ. Пусть А и В – постоянные. Тогда справедливо равенство
![]()
Это
свойство обобщается на любое число
слагаемых. Пусть
![]() –
некоторые функции, C
–
некоторые функции, C![]() , …, C
, …, C![]() –
постоянные. Тогда верно равенство
–
постоянные. Тогда верно равенство
![]() .
.
Вычисление НИ, использующее только линейное свойство НИ, табличные интегралы и легко проверяемую формулу
![]() ,
(1)
,
(1)
где F – первообразная f, называют непосредственным интегрированием.
Рассмотрим примеры. Вычислить следующие интегралы.
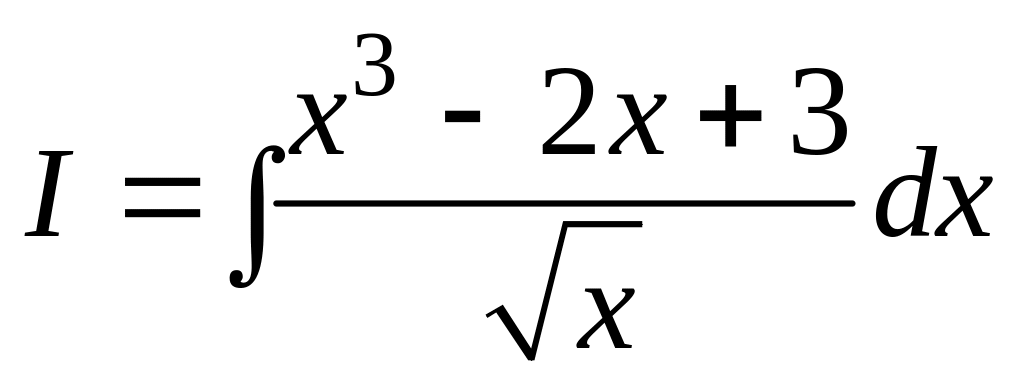 .
.
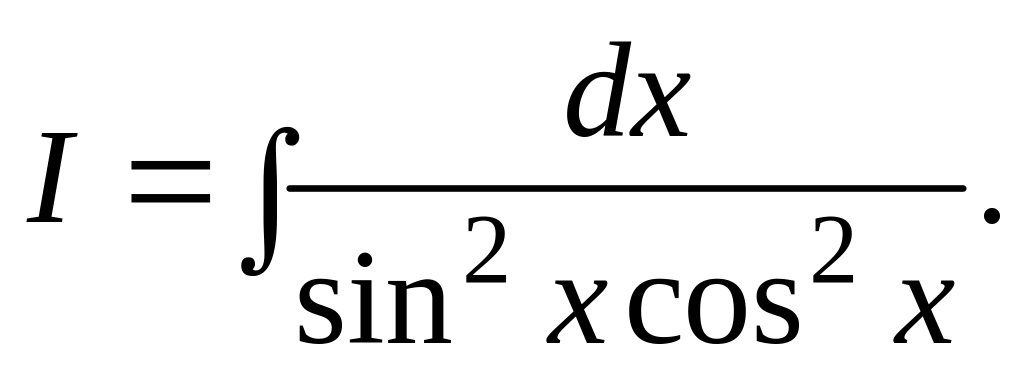
I =
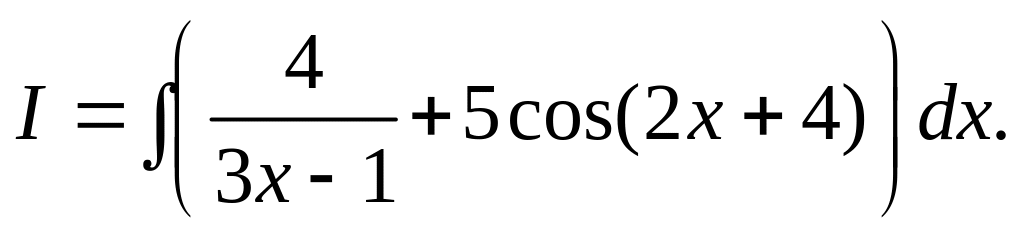
Решение.
Поделив числитель на знаменатель почленно, получим
![]()
Представим числитель в виде
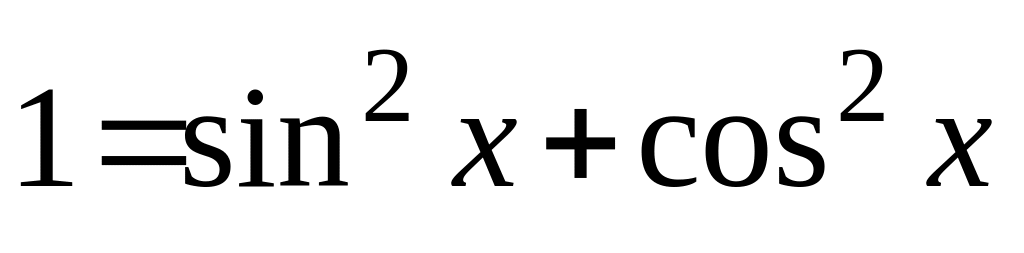 и поделим числитель на знаменатель
почленно. Получаем
и поделим числитель на знаменатель
почленно. Получаем
![]()
Используя свойство линейности интеграла и формулу (1), запишем
![]()
При вычислении интегралов от выражений, состоящих из тригонометрических функций, полезны следующие формулы:
sin
αx
cos
βx
=
![]()
sin
αx
sin
βx
=
![]()
cos
αx
cos
βx
=
![]()
cos![]() sin
sin![]() 1 + tg
1 + tg![]()
Рассмотрим примеры.
1.4.
![]()
Решение. Преобразуем подынтегральную функцию следующим образом:
сos
x
sin
2x·cos 4x
=
![]() (sin
x +
sin
3x)
cos
4x
=
(sin
x +
sin
3x)
cos
4x
=
= ![]() (–sin 3x
+ sin 5x
– sin x
+ sin 7x).
(–sin 3x
+ sin 5x
– sin x
+ sin 7x).
Тогда
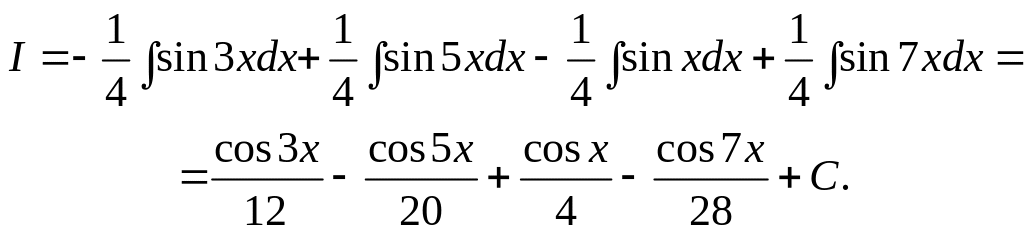
1.5.
![]()
Решение.
Используя тригонометрическую формулу
![]()
![]() ,
преобразуем подынтегральную функцию
и вычисляем интеграл
,
преобразуем подынтегральную функцию
и вычисляем интеграл
![]()
I =

Решение.
Преобразуем подынтегральную функцию,
используя формулу
![]() ,
а затем, применяя аналогичную формулу
к
,
а затем, применяя аналогичную формулу
к
![]() ,
вычисляем интеграл
,
вычисляем интеграл
![]()
![]()
=![]()
