
11. 2. Распределение Бозе - Эйнштейна для фотонного газа
Равновесное тепловое излучение в замкнутой полости представляет собой совокупность стоячих электромагнитных волн с дискретными частотами.
Попытки теоретически объяснить наблюдаемое распределение спектральной плотности излучения по частотам с классической точки зрения оказались несостоятельными и породили так называемую «проблему теплового излучения».
В 1900 г. она была решена Планком путем введения в процесс взаимодействия излучения с веществом идеи квантования.
Эйнштейн сделал следующий шаг. Он предположил, и это подтвердилось экспериментом, что само излучение представляет собой фотонный газ, газ идеальный.
У фотонов спин равен единице. Значит это бозоны, а они подчиняются статистике Бозе - Эйнштейна.
Число фотонов в полости не сохраняется, оно зависит от температуры. А для систем с переменным числом бозонов химический потенциал = 0, и функция (3) принимает вид (5), т.е.
.
Для фотонов = h и р=h/c, поэтому число квантовых состояний (фазовых ячеек) в интервале частот (, +d) в расчете на единицу объема фотонного газа равно согласно (7)
![]() .
.
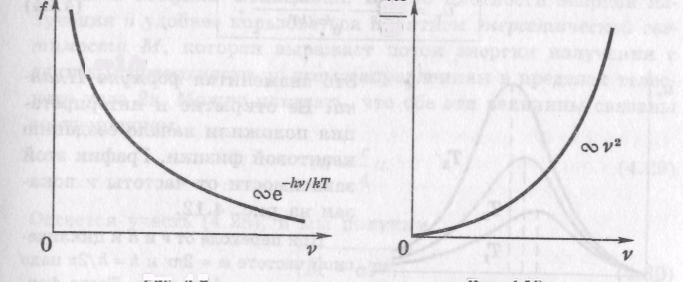 Рис.
7 и рис. 8.
представлены
графики
функций f
и
dZ/d
для фотонного газа
Следует
обратить внимание на то, что
обе функции ведут
себя с ростом частоты
взаимно противоположно:
Рис.
7 и рис. 8.
представлены
графики
функций f
и
dZ/d
для фотонного газа
Следует
обратить внимание на то, что
обе функции ведут
себя с ростом частоты
взаимно противоположно:
f убывает, a dZ/d растет.
В
соответствии с формулой (8) число
фотонов с частотами в интервале
(,
+ d)
равно![]() .
.
Коэффициент 2
появился в связи с двумя независимыми поляризациями излучения во взаимно перпендикулярных плоскостях.
Другими словами, он указывает на две возможные поперечные поляризации фотона. Напомним, что в случае электронов этот коэффициент учитывал две возможные «ориентации» спина электрона.
 рис.9.
График распределения фотонов по частотам,
т.е. dn/d.
рис.9.
График распределения фотонов по частотам,
т.е. dn/d.
Площадь под кривой равна полному числу n фотонов в расчете на единицу объёма фотонного газа.
Теперь перейдем к спектральной плотности энергии излучения (фотонного газа): u = du/d, где du = h dn.
В
результате получим:![]() . (17)
. (17)
Это знаменитая формула Планка.
 Её
открытие и интерпретация
положили начало созданию квантовой
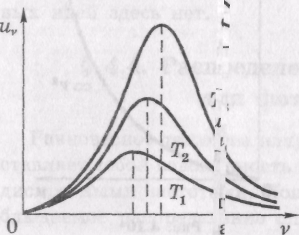
физики. График
этой зависимости
от частоты
показан
на рис.10.
Её
открытие и интерпретация
положили начало созданию квантовой
физики. График
этой зависимости
от частоты
показан
на рис.10.
При переходе от и h к циклической частоте = 2 и надо учесть, что ud = ud.
Тогда формула Планка приобретает вид:
![]()
![]() .
.
Вернемся к формуле (17), графики которой при разных температурах представлены
на
рис. 10, где T![]() <
Т2
< Т3.
<
Т2
< Т3.
Площадь под каждой из этих кривых равна полной плотности энергии u при соответствующей температуре.
Выясним, как эта величина зависит от Т. Для этого представим (17) в виде:
u![]() =
=
![]() ,
,
где F — функция, вид которой до открытия Планка был неизвестен.
В таком виде формула была получена Вином и получила название формулы Вина. Тогда:
u=![]() ,
,
здесь введена новая временная х = /T.
Последний интеграл представляет собой некоторую постоянную a , и мы приходим к выводу, что
u=aТ
![]() .Закон
Стефана-Больцмана.
.Закон
Стефана-Больцмана.
Вместо плотности энергии излучения u удобнее пользоваться понятием энергетической светимости R, которая выражает поток энергии излучения с единицы поверхности по всем направлениям в пределах телесного угла 2. Можно показать, что обе эти величины связаны соотношением
![]()
Тогда
![]() .
Эта
формула и выражает закон
Стефана-Больцмана.
.
Эта
формула и выражает закон
Стефана-Больцмана.
Здесь - постоянная Стефана-Больцмана.
С помощью формулы Планка можно найти ее зависимость от постоянных с, h, k и ее числовое значение:
=
5.6710![]()
![]() Вт/(м
Вт/(м![]() K
)
K
)
Если в стенках полости с равновесным тепловым излучением (фотонным газом) сделать небольшое отверстие, то можно экспериментально исследовать спектральный состав выходящего через это отверстие излучения. Это было проделано для разных температур полости. Результаты оказались в прекрасном соответствии с формулой Планка и законом Стефана-Больцмана.
Закон смещения Вина.
При теоретических исследованиях спектральный состав излучения удобнее характеризовать по частотам, в экспериментальных же - по длинам волн.
Имея в
виду соотношение ud
=-u![]() d,
и
= с/,
запишем:
d,
и
= с/,
запишем:
u![]() =
- u
=
- u
![]() =
=![]() F(λT)
F(λT)![]() =
=![]() .
.
Наличие знака
минус в исходной
формуле связано с тем, что с
ростом
частоты (d>0)
длина волны уменьшается (![]() ).
).
Найдем
теперь длину волны т,
соответствующую
максимуму
функции
![]()
Это значит, надо решить уравнение
![]()
Выражение в скобках есть некоторая функция Ф(Т).
При длине волны т соответствующей максимуму функции u , функция Ф(Т) должна обратиться в нуль: Ф(тТ) = 0. Решение последнего уравнения приводит к некоторому значению b величины тТ .
Таким образом, можно записать, что Tт=b . Это и есть закон смещения Вина.
Значение постоянной b можно найти экспериментально или с помощью формулы Планка:b=0,29 смK .
С ростом температуры длина волны т уменьшается, а значит, частота m увеличивается, как показано на рис. 10.
Заметим только, что m с/т , поскольку m соответствует распределению по частотам, а т - по длинам волн.
С помощью закона смещения Вина легко определить температуру Т электромагнитного излучения (или его источника), спектр которого соответствует формуле Планка.
Так находят, например, температуру звезд.
