Тема 11. Диференціал функції однієї змінної.

1. Означення диференціала функції.

2. Геометричний зміст диференціала.

3. Правила обчислення диференціалів функцій.

4. Інваріантність диференціала першого порядку.

5. Диференціали вищих порядків.

Д иференціал, границя, збіжність, нескінченно мала величина, інваріантність, порядок диференціала.

Диференціалом функції називається головна лінійна відносно Δх частина приросту функції в точці х:

.

о(х) – нескінченно мала величина вищого порядку малості порівняно з Δх.

Властивість диференціала першого порядку зберігати зовнішній вигляд у випадку складної функції називають інваріантністю його форми.

Диференціали вищого порядку ( ) вже не мають властивості інваріантності форми:

1) для незалежної змінної u:

;

2) для u = φ(x):

.

Основна: . Додаткова: .

1. Дайте означення поняття «диференціал»?

2. Як пов’язаний диференціал з похідною?

3. Як отримати диференціал функції вищого порядку?

4. В чому зміст інваріантності форми диференціала першого порядку?

5. Чи впливає порядок диференціала на властивість інваріантності форми?

Тема 12. Основні теореми диференціального числення.

1. Теорема Ролля.

2. Теорема Лагранжа.

3. Наслідки з теореми Лагранжа.

4. Теорема Ферма.

5. 1-е і 2-е правила Лопіталя.

Н еперервність, найбільше значення функції, найменше значення функції, похідна, кутовий коефіцієнт, диференційовність, границя.

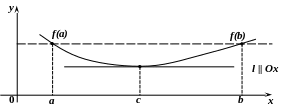
Нехай функція f(x) неперервна на відрізку [a, b], диференційовна на інтервалі (a, b), і f(a) = f(b). Тоді існує принаймні одна точка с  (a, b) така, що f'(c) = 0 (теорема Ролля).

Доведення

Я кщо деяка функція f(x) неперервна на замкнутому проміжку, то вона набуває на цьому проміжку принаймні один раз свого найбільшого М і найменшого m значення.

l

Теорема Лагранжа: Нехай функція f(x) неперервна на відрізку [a, b] і диферен-ційовна на інтервалі (a, b). Тоді існує принаймні одна точка с  (a, b) така, що

.

Доведення

s || l

Я кщо точка х₀ є точкою екстремуму функції f(x) і в цій точці диференційовна, то f'(x) = 0 – необхідна умова існування екстремуму (теорема Ферма).

Д ослідимо на екстремум функцію .

Згідно з теоремою Ферма, перевіримо необхідну умову його існування. Для цього продиференціюємо функцію і прирівняємо першу похідну до нуля:

.

Розв’язавши квадратне рівняння, отримаємо:

.

Отже, це і є точки можливих екстремумів. Використання програми будування графіків дозволяє в цьому упевнитися (див. рисунок).

1 -е правило Лопіталя: Нехай функції f(x) i g(x) диференційовні на інтервалі (a,b); , і g'(x)  0 на (a, b). Тоді при існуванні скінченної або нескінченної границі границя теж існує, причому .

1-е правило Лопіталя залишається в силі, якщо .

2 -е правило Лопіталя: Нехай функції f(x) i g(x) диференційовні на інтервалі (a,b); , і g'(x)  0 на (a, b). Тоді, якщо існує скінченна або нескінченна границя , то границя теж існує, причому .

Я кщо для похідних обох функцій f(x) і g(x) виконуються умови 2-го правила Лопіталя, то саме правило можна застосовувати повторно.

Д ослідити на існування границі при умові вираз .

Оскільки при виконанні умови границя і чисельника, і знаменника існує й дорівнює нулю, то виникає невизначеність типу . Застосуємо правило Лопіталя:

.

Основна: . Додаткова: .

1. В чому полягає основний зміст теореми Ролля?

2. Доведіть теорему Лагранжа.

3. Як формулюється необхідна умова існування екстремуму функції?

4. Як знайти границю відношення типу 0/0 чи /?

5. Чи можна застосовувати правила Лопіталя повторно?