Тема 4. Необхідні і достатні умови екстремуму.

Метод найменших квадратів.

§1. Необхідна і достатня умова екстремуму.

Алгоритм знаходження екстремуму.

Мета оптимізації - це обчислення максимумів та мінімумів економічних функцій. Обмежимося випадком функції двох змінних.

Число М називають максимумом функції y = f(x₁, x₂) на множині Х, якщо існує така пара (а₁,а₂) значень аргументу х₁, х₂ для якої: f(a₁, a₂) = M  f(x₁, x₂) Точка (a₁, a₂) - називається точкою максимуму.

Аналогічно визначається мінімум функції ,число -m

f(a₁, a₂) = m< f(x₁, x₂)

Максимуми та мінімуми позначають відповідно символами: M =max f(x₁ ,x₂) ; m =min f(x₁ ,x₂) і називають одним терміном “екстремум”. Означені таким чином екстремуми локальні, бо мова йде про максимуми та мінімуми лише в достатньо малому околі точки М₀(a₁, a₂).

Необхідна умова екстремуму.

Якщо диференційована функція f досягає екстремуму в точці М₀, то в цій точці = 0; де k = 1, 2,  n.

Необхідну умову екстремуму можна перефразувати так:

В точці мінімуму або максимуму диференційованої функції градієнт дорівнює нулю.

Або

В точці екстремуму перетворюються в нуль похідні по всім напрямкам.

Рівність частинних похідних нулю виражає лише необхідну, але не достатню умову екстремуму функції багатьох змінних.

Наприклад, частинні похідні в “сідлових” точках М₀ (х₀; у₀):

f_x (х₀; у₀) = 0; f_y(х₀; у₀) = 0, але очевидно ніякого екстремуму в точці М₀ (х₀; у₀) нема. Такі “сідлові” точки є двовимірними аналогами точок перегину функції однієї змінної. Задача полягає в тому, щоб відокремити їх від точок екстремуму. Іншими словами необхідно знати достатню умову екстремуму

.

z M(x₀; y₀)

у

0

x

Достатні умови екстремуму.

Нехай - стаціонарна точка функції , причому ця функція двічі диференційована в деякому околі точки і всі її другі частинні похідні неперервні в точці . Тоді:

а). Якщо як функція має сталий знак при будь яких наборах значень , не рівних одночасно нулю, то функція має в точці екстремум, а саме:

максимум при 0 і

мінімум при  0.

б). Якщо є знакозмінною функт

ією , тобто набуває як додатних так і від’ємних значень, то точка не є точкою екстремуму функції

в). Якщо  0

 0

причому існують такі набори значень не рівних одночасно нулю, для яких значення другого диференціала дорівнює нулеві, то функція в точці може мати екстремум, але може і не мати його.

У випадку функції двох змінних достатні умови екстремуму можна сформулювати по іншому.

Нехай - стаціонарна точка функції і ; ; ; , тоді

1). Якщо   0, то - точка екстремуму, причому

при  0 – точка максимуму

при  0 – точка мінімуму

2). Якщо   0, то в точці екстремуму нема.

У випадку  = 0 функція f в стаціонарній точці екстремум може мати або ні. Необхідні додаткові дослідження.

Зауваження: Точки в яких = 0 називаються стаціонарними або критичними точками функції

Наприклад: Знайти стаціонарні точки

Розв’язання:

, то координатами стаціонарній точки будуть розв’язки системи

Алгоритм обчислення екстремумів функції двох змінних

1). Обчислимо стаціонарні точки, розв’язавши систему двох рівнянь з двома невідомими

Зауваження: Частіш за все для розвязання такої системи застосовують чисельні (наближені) методи.

2). Обчислимо значення частинних похідних другого порядку в знайдених стаціонарних точках

,

; ; ;

3). Визначимо “знак” виразу

Якщо   0 і  0,  0, то в стаціонарній точці (а; в) матимемо мінімум.

Якщо   0 і  0,  0, то в стаціонарній точці (а; b) матимемо максимум.

Якщо   0, то в стаціонарній точці не буде ні максимуму ні мінімуму.

Інші випадки  = 0 потребують додаткових досліджень.

Зауваження: Для функції n змінних стаціонарні точки обчислюють з розвязку системи рівнянь.

Приклад 1. Знайти екстремум функції

Маємо

Скориставшись необхідною умовою екстремуму, знаходимо стаціонарну точку

або   М₀ (21;20)

Знайдемо значення других похідних у точці М₀

, тоді

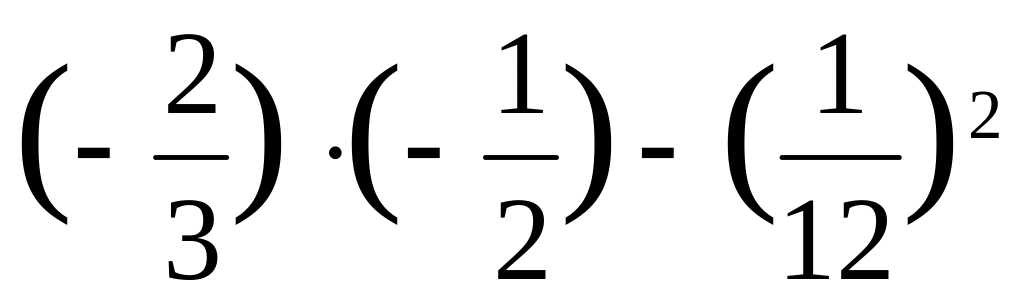= =  0

Оскільки А  0, то в точці М₀ (21; 20) функція має максимум

Приклад 2. Знайти екстремуми функції

Розв’язання:

; ; 

(1; 1); (1; -1); (-1; 1); (-1; -1).

; ; , обчислимо їх значення в кожній критичній точці та перевіримо в ній виконання достатньої умови екстремуму.

Наприклад, в точці (1; 1): ; В= 0 ; С =-2 

 = (-2)² - 0 = 4  0; А = -2  0  (1; 1) є точкою максимуму. Аналогічно (-1; -1) – точка мінімуму

для яких  0, екстремуму нема, тобто ці точки є сідловими.

Приклад 3. Невелика фірма виробляє два види товарів G₁ і G₂ та продає їх по цінам 1000 і 800 відповідно. Функція витрат має вигляд: C= 2Q₁² + 2Q₁ Q₂ + Q₂² де Q₁ і Q₂ позначають об’єми випуску відповідно товарів G₁ і G₂. Необхідно знайти такі значення Q₁ і Q₂ ,при яких прибуток фірми буде максимальним.

Розв’язання

В зв’язку з тим , що фірма невелика, вона не може монопольно встановлювати ціни і повинна орієнтуватись на ринкові ціни, які не залежать від об’ємів виробництва Q₁ і Q₂ ( ці об’єми занадто малі).Тому сумарний доход R від продажу товарі

R= 1000Q₁ + 800Q₂ Прибуток S являє собою різницю між доходом R і витратами C , тому :

S = R – C = (1000Q₁ + 800Q₂) - (2Q₁² + 2Q₁Q₂ + Q₂² ), або

S(Q_1, Q₂ ) = 1000Q₁ + 800Q₂ - 2Q₁² - 2Q₁ Q₂ - Q₂²

Дослідимо отриману функцію на екстремуми по відповідному алгоритму

1). (Q_1, Q₂ ) = 1000 - 4Q₁ - 2Q₂

(Q_1, Q₂ ) = 800 - 2Q₁ - 2Q₂

200 = 2Q₁ ; Q₁ = 100 ; Q₂ = 300 ; Таким чином стаціонарна точка має координати М₀ =(Q_1, Q₂ )=(100; 300)

2). Залишається з’ясувати: матимемо ми в стаціонарній точці максимум , мінімум чи не матимемо ні того ні іншого. Для розв’язку обчислимо частинні похідні другого порядку

Складаємо вираз:

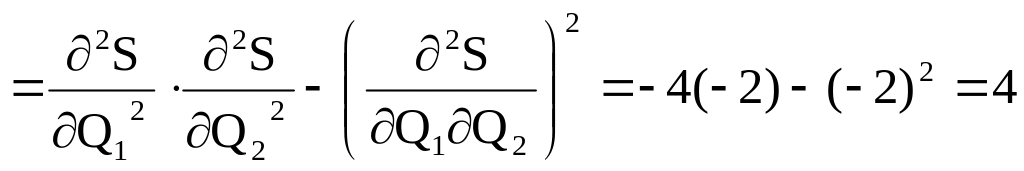  0

окрім того :  0;  0,

тому в стаціонарній точці має місце максимум.

Підставляючи координати стаціонарної точки в функцію прибутку, отримаємо:

S(100; 300) = 1000100 + 800300 - 2100² - 2100300 - 300² = 170000

Це і буде величина максимального прибутку, що досягається при об’ємах виробництва Q₁ = 100 ,Q₂ = 300

Приклад 4. Фірма реалізує частину товару на внутрiшньому ринку , а другу частину поставляє на експорт. Зв’язок ціни товару Q₁ та його кількості Р₁, проданого на внутрішньому ринку, описується кривою попиту з рівнянням Р₁+ Q₁ = 500. Аналогічно для експортних товарів їх ціна Q₂ та кількість Р₂ пов’язані залежністю 2 Р₂ +3 Q₂ =720

Сумарні витрати задаються виразом : С = 50 000 + 20(Q₁+ Q₂)

Необхідно розрахувати якої цінової політики повинна дотримуватись фірма, щоб її прибутки були максимальними .