2.2. Неперервна (одновимірна) випадкова величина

На початку цього розділу ми ознайомилися з по­няттям випадкової величини, і там було зазначено, що випадкова величина Х називається неперервною, якщо її можливі значення суцільно заповнюють деякий скінченний або нескінченний проміжок на числовій прямій. Наведене поняття неперервної випадкової величини ми далі уточнимо. Нагадаємо також, що в разі, коли випадкова величина є дискретною, то закон розподілу цієї змінної повністю визначається переліком її можливих значень та від­повідних їм імовірностей.

Однак для неперервної випадкової величини, яка має незліченну множину можливих значень, така характеристика розподілу непридатна. Дійсно, якщо випадкова величина Х має значення, що суцільно заповнюють інтервал , то записати її закон розподілу у вигляді переліку мождивих значень та відповідних їм імовірностей неможливо хоча б з тієї причини, що в цьому випадку неможливо скласти перелік її значень. Тому потрібно звернутися до загального способу характеристики розподілу такої величини. З цією метою вводиться поняття функції розподілу ймовірностей випадкової величини.

2.2.1. Функція розподілу ймовірностей

Нехай X – будь-яка випадкова величина і x – до­вільне дійсне число.

Означення. Функцією розподілу ймовірностей (функцією розподілу) випадкової величини X називається ймовірність того, що в результаті випробування вона набуде значення, меншого за число x, тобто

(2.11)

Геометрично рівність (2.11) можна трактувати так: є ймовірність того, що випадкова величина X набуває значень, які зображаються на числовій прямій точками, що лежать зліва від точки x.

Функцію розподілу ймовірностей випадкової величини називають ще інтегральною функцією.

Тепер уточнимо означення неперервної випадкової величини: випадкову величину називають неперервною, якщо її функція розподілу є неперервна і кусково-диференційовна.

Нагадаємо, що функція є кусково-диференційовна, якщо вона має непе­рервну похідну всюди, крім, можливо, скінченного числа точок.

Наприклад, такою функцією є 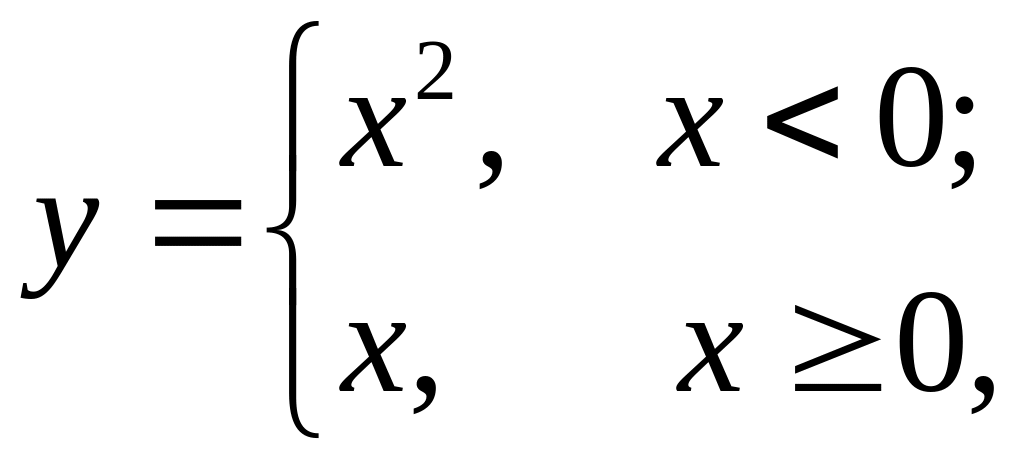яка має неперервну похідну для всіх і для всіх . У точці похідна цієї функції має розрив першого роду, бо і , а сама функція є неперервна в цій точці. (Проілюструйте наведенні міркування на графіку даної функції).

Зауважимо ще раз, що поняття функції розподілу ймовірностей вводиться для будь-якої випадкової величини Х, у т. ч. дискретної, тільки в цьому випадку вона не є неперервною.

Приклад 2.9. Дискретна випадкова величина X має закон розподілу ймовірностей, що заданий таблицею:

	-2	1	4	6
	0,2	0,1	0,3	0,4

Знайти функцію розподілу і нарисувати її графік.

Розв’язання. Якщо то , бо подія неможлива.

Якщо то бо подія X < x є рівносильна події Х = –2, яка має ймовірність 0,2.

Якщо то бо подія є сумою двох несумісних подій: , що має ймовірність , і , яка має ймовірність

Якщо то бо подія у даному випадку є сумою трьох несумісних подій: , яка має ймовірність яка має ймовірність , і X = 4, яка має ймовірність

Якщо то бо подія є вірогідною.

Отже, функція розподілу заданої дискретної випадкової величини має такий ана­літичний вигляд:

Графік цієї функції (рис. 2.1) показує, що функція розподілу дискретної випадкової величини має «східчастий» характер.

Р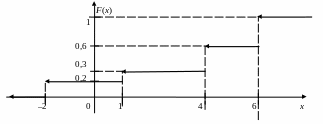 ис. 2.1. Графік функції розподілу дискретної випадкової величини до прикладу 2.9

Властивості функції розподілу:

1. Значення функції розподілу належать відрізку [0, 1], тобто:

0 F(x) 1.

Це випливає з того, що є імовірність події і її значення належать проміжку .

2. Якщо x₁ < x₂, то , тобто F(x) – неспадна функція.

Справді, нехай . Подія є сумою двох несумісних подій та , тобто . За теоремою додавання ймовірностей несумісних подій маємо:

.

Оскільки , то , що і потрібно було обгрунтувати.

3. , тобто функція F(x) – неперервна зліва.

Доведення цієї властивості опускаємо.

4. Якщо можливі значення випадкової величини Х належать інтервалу , то при і при .

Дійсно, якщо , то подія є неможлива, величина Х не набуває значень, які менші за число , і тому .

Якщо , то подія є вірогідна, оскільки всі можливі значення величини Х є менші , і тому .

Зауважимо, що звідси випливає таке твердження: якщо можливі значення неперервної випадкової величини розміщені на всій осі Ох, то виконуються такі співвідношення:

, .

5. Імовірність того, що випадкова величина X набуде значення з проміжку [а, b), дорівнює приросту її функції розподілу на цьому проміжку, тобто:

. (2.12)

Дане твердження одержуємо з рівності

(див. доведення властивості 2), поклавши в ній і .

6. Якщо випадкова величина Х неперервна, то ймовірність того, що вона набуде будь-якого окремого значення, дорівнює нулю, тобто для будь-якого значення х₀.

Справді, прийнявши у наведеній у попередній властивості нерівності і , маємо:

.

Якщо , то з неперервності функції випливає, що , а це означає, що .

Отже, говорити про ймовірність того, що неперервна випадкова величина набуде одного певного зі своїх можливих значень немає сенсу, а слід говорити тільки про ймовірність попадання її значень у деякий (навіть як завгодно малий) проміжок.

Дане твердження повністю відповідає вимогам практичних задач, наприклад, при виготовленні деталей з’ясовують імовірність того, що розміри деталей не виходять за дозволені межі, і не ставлять питання про імовірність їх співпадання з проектними розмірами.

7. Якщо випадкова величина Х неперервна, то для будь-яких дійсних чисел а і b, правильні рівності:

(2.12´)

Дані рівності випливають безпесоредньо з (2.12) та властивості 6, бо, наприклад,

.

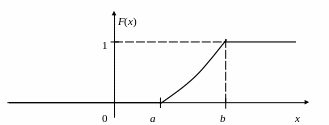
Наведені властивості функції розподілу неперервної випадкової величини дозволяють описати її графічне зображення. Припустімо, що всі значення випадкової величини Х зосереджені в інтервалі (а, b). Тоді графік функції розподілу F(x) буде такий, як на рис. 2.2.

Рис. 2.2. Графік функції розподілу неперервної випадкової величини

Приклад 2.10. Випадкову величину X задано функцією розподілу:

Н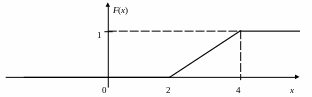 арисувати її графік та обчислити ймовірності:

Розв’язання. Будуємо графік функції (рис. 2.3):

Рис. 2.3. Графік функції розподілу до прикладу 2.10

Шукані ймовірності обчислюємо за формулою (2.12′):

131