2.1.3. Чисельні характеристики

Закон розподілу ймовірностей повністю характер­ризує дискретну випадкову величину, однак він не завжди відомий, і ми вимушені обмежуватися в цих випадках меншими відомостями про неї. Поряд із тим, іноді навіть зручніше користуватися числами, які описують випадкову величину сумарно, і вони називаються чисельними характе­ристиками цієї величини. Розглянемо основні з них.

А. М а т е м а т и ч н е с п о д і в а н н я. Припустімо, що дискретна випадкова величина X може набувати значень з імовірностями , тобто вона описується законом розподілу у формі таблиці (див. табл. 2.1).

Означення. Математичним сподіванням M(X) дискретної випадкової величини X називається сума добутків усіх можливих її значень на їх імовірності, тобто

(2.3)

Якщо множина значень дискретної випадкової величини X є нескінченна і зліченна, то

причому математичне сподівання існує, якщо ряд справа у рівності збіжний абсолютно.

Зауважимо, що значення математичного сподівання випадкової вели­чини не є випадкове [М(Х) – стала величина].

Приклад 2.4. Закон розподілу дискретної випадкової величини Х задано таблицею:

Х = хі	-4	-3	2	3	6	8
р = рі	0,1	0,1	0,2	0,3	0,1	0,2

Обчислити М(Х).

Розв’язання. За формулою (2.3):

Математичне сподівання має такі основні властивості:

1. Математичне сподівання сталої величини дорівнює цій величині, тобто якщ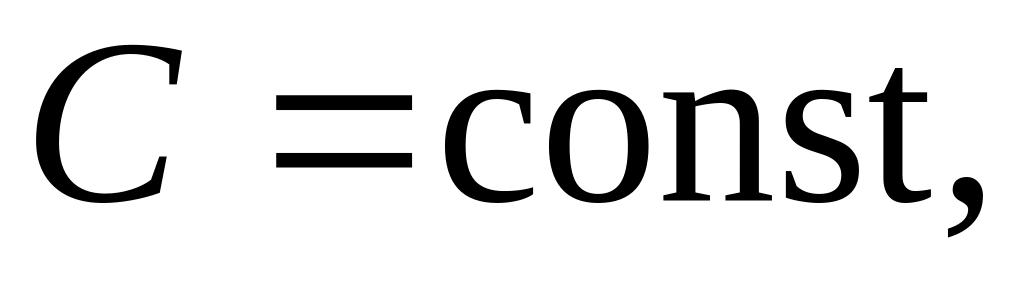о то .

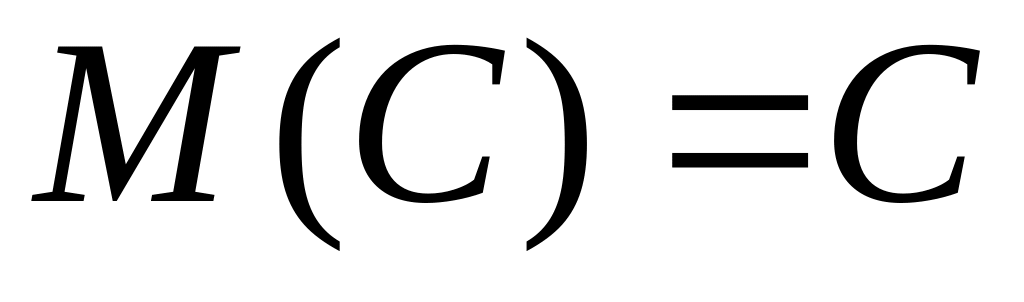Дійсно, сталу величину Х розглядатимемо як дискретну випадкову величину Х, яка набуває одного значення C з імовірністю р=1. Тому

.

2. Сталий множник виноситься за знак математичного сподівання, тобто якщо то

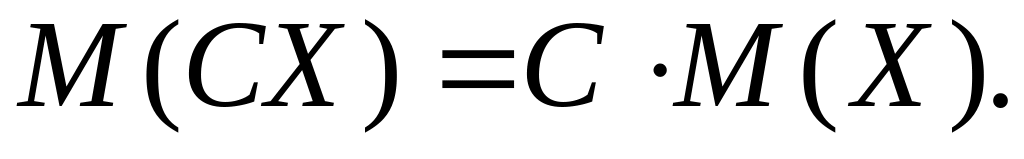
Нехай дискретна випадкова величина Х задана законом розподілу

			...
			...

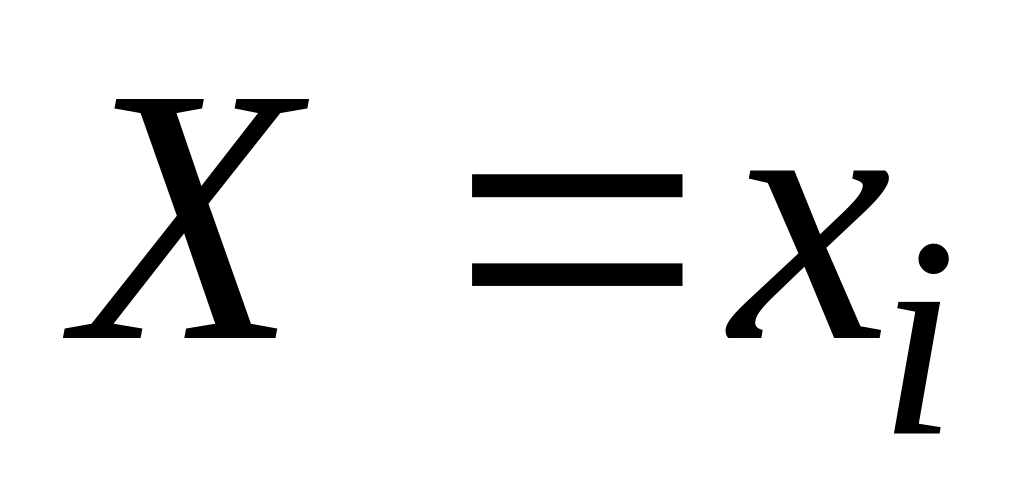
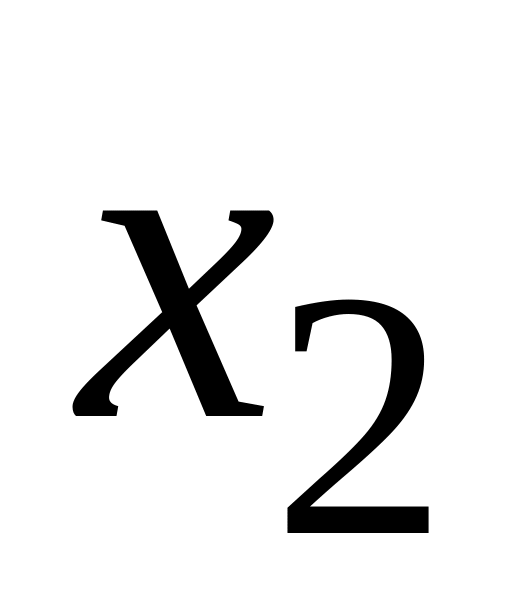
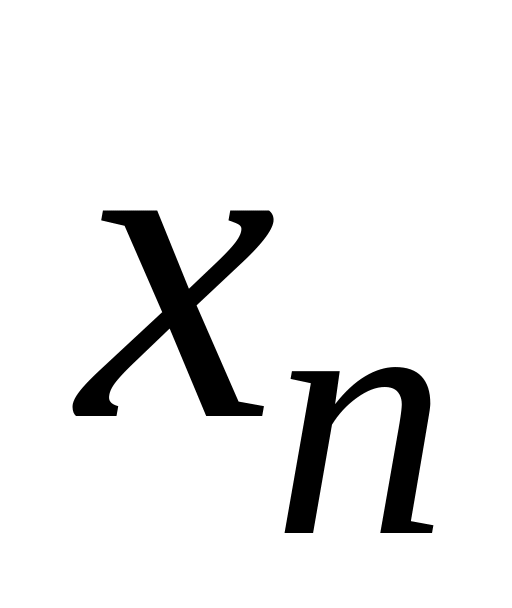
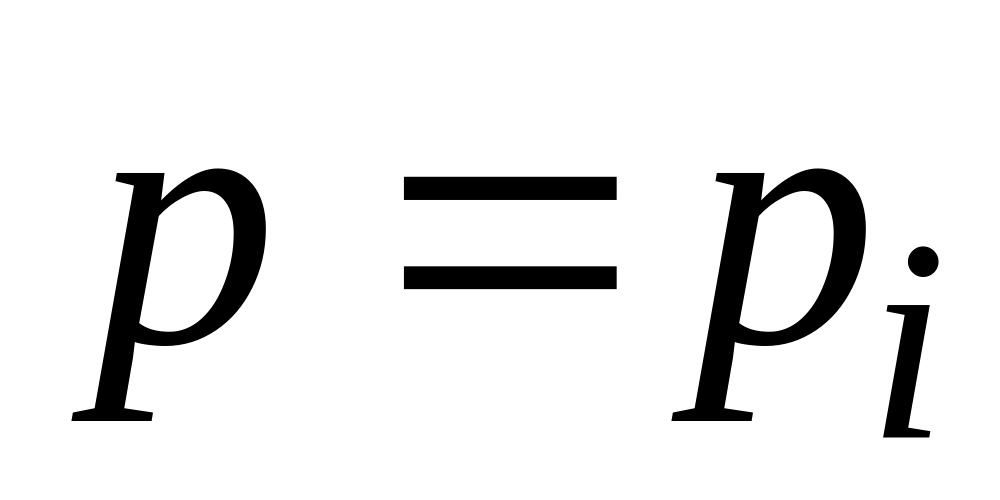
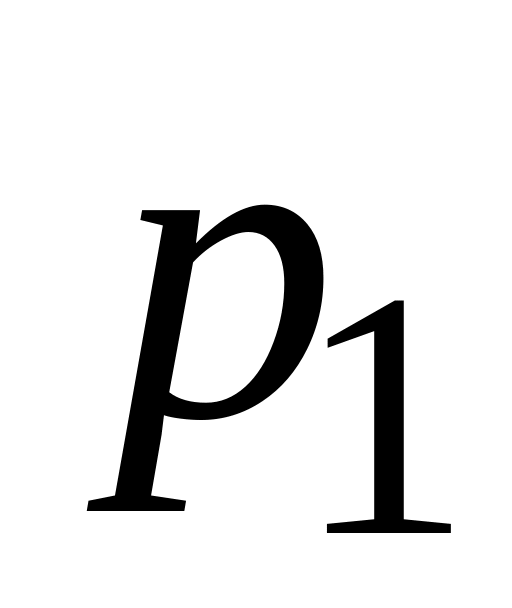
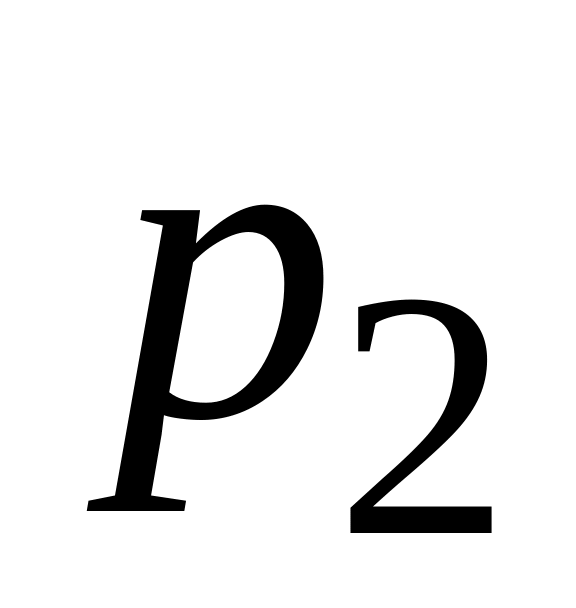
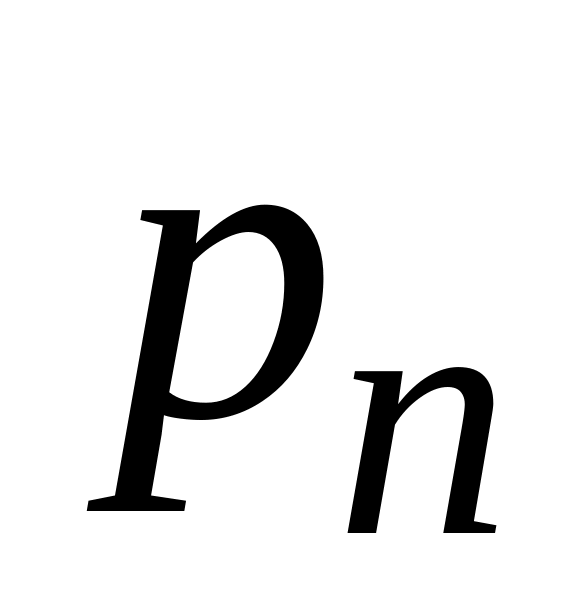
Добуток сталої величини С на дискретну випадкову величину Х є дискретна випадкова величина СХ, яка набуває значень з імовірностями . Тому

.

3. Математичне сподівання алгебраїчної суми двох (або кількох) ви­падкових величин дорівнює алгебраїчній сумі математичних споді­вань цих величин, тобто .

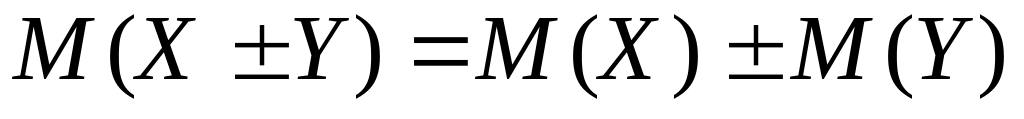Нехай випадкові величини Х та Y задані законами розподілу:

			...						...
			...						...

Запишемо всі можливі значення величини та їх імовірності .

За формулою (2.3) маємо:

.

Далі обгрунтуємо рівності:

Імовірність того, що випадкова величина Х набуде значення дорівнює . Подія може відбутися, якщо величина набуде значень або , ..., або і ці події є несумісні. Тому за правилом додавання ймовірностей несумісних подій маємо, що

.

Аналогічно, подія (її ймовірність ) є сумою несумісних подій ..., (їх імовірності відповідно дорівнюють і тому за тим же правилом додавання імовірностей несумісних подій

.

Використовуючи ці рівності маємо:

Врахувавши властивість 2, одержуємо:

.

4. Математичне сподівання добутку двох незалежних випадкових величин (або кількох взаємно незалежних випадкових величин) дорівнює добуткові математичних сподівань цих величин, тобто якщо 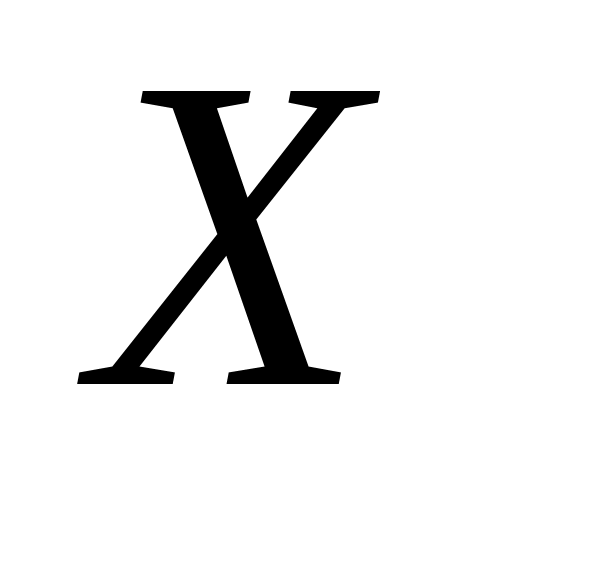і Y – незалежні випадкові величини, то .

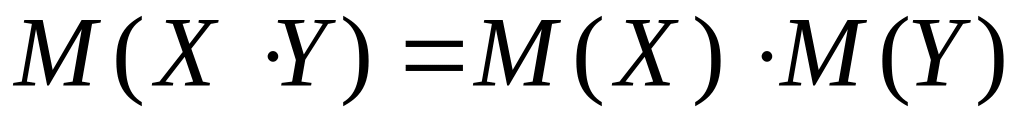Нехай випадкові величини Х та Y задані законами розподілу:

			...						...
			...						...

Можливі значення випадкової величини є: . Позначивши через - відповідні ймовірності цих значень, за формулою (2.3) маємо:

.

Враховуючи, що випадкові величини Х і Y – незалежні (це рівносильно тому, що події і є незалежні), маємо:

.

Тому математичне сподівання випадкової величини XY можемо записати у вигляді:

Зауваження. Властивості 3 і 4 поширюються на випадок довільного числа дискртених випадкових величин, а саме:

• математичне сподівання алгебраїчної суми декількох випадкових величин дорівнює сумі їх математичних сподівань, тобто:

;

• математичне сподівання добутку декількох взаємно незалежних випадкових величин дорівнює добутку їх математичних сподівань, тобто

.

Сформульовані твердження можна довести методом математичної індукції.

Імовірнісний зміст математичного сподівання: математичне споді­вання випадкової величини Х наближено дорівнює середньому арифметич­ному зваженому її спостережуваних значень.

Справді, розглянемо дискретну випадкову величину Х, закон розподілу якої задано табл. 2.1. Нехай проводиться N незалежних експериментів, у кожному з яких випадкова величина Х набуває деякого значення з множини {x₁, x₂, …, x_n}. Припустімо, що значення х₁ набуте N₁ разів, значення x₂ набуте N₂ разів, …, значення x_n набуте N_n разів. Тоді середнє арифметичне зважене обчислимо за формулою:

Відношення є відносна частота (статистична ймовірність) події і тому

тобто середнє арифметичне зважене спостережуваних значень випадкової величини дорівнює сумі добутків її можливих значень на відповідні їм відносні частоти.

Вивчення статистичної ймовірності випадкової події показало, що за необмеженого збільшення числа експериментів N відносна частота w_і цієї події буде наближатися до її ймовірності , тобто за великих N маємо наближену рівність w_і ≈ p_i. Тому і середнє арифметичне зважене буде в цьому випадку також наближатися до математичного сподівання М(Х), тобто

. (2.3)

А це означає, що за досить великого числа експериментів середнє арифметичне спостережуваних значень випадкової величини Х можна при­йняти рівним її математичному сподіванню.

Зауважимо, що математичне сподівання М(Х) випадкової величини Х є точка числової прямої, в околі якої «розсіяні» її значення

Приклад 2.5. Молокозавод має договори на постачання молока з трьома фермерами і двома агрофірмами. Імовірність виконання договору одним фермером становить 0,8, а однією агрофірмою – 0,6. Знайти середню кількість постачальників сировини, які виконають договори.

Розв’язання. Нехай X – число фермерів і Y – число агрофірм, що виконають договори. Складемо закони розподілу цих дискретних випадкових величин.

Для випадкової величини X маємо: і можливі значення Імовірності обчислюємо за формулою Бернуллі:

Перевірка:

Закон розподілу випадкової величини X має форму такої таблиці:

Х = xi	0	1	2	3
р = pix	0,008	0,096	0,384	0,512

Для випадкової величини Y маємо: і можливі значення . Імовірності обчислимо також за формулою Бернуллі:

Перевірка:

Закон розподілу випадкової величини Y має вигляд:

Y = yi
р = piy	0,16	0,48	0,36

За ймовірнісним змістом математичного сподівання середнє число поста­чальників молока наближено дорівнює , тобто

Отже, середнє число постачальників дорівнює 3–4.

Зауваження. У разі проведення послідовності експериментів (випро­бувань) за схемою Бернуллі математичне сподівання числа появ події (випадкова величина Х) у цих випробуваннях обчислюється за спро­щеними формулами:

• математичне сподівання числа Х появ події в одному випробуванні дорівнює ймовірності р появи події в цьому випробуванні, тобто

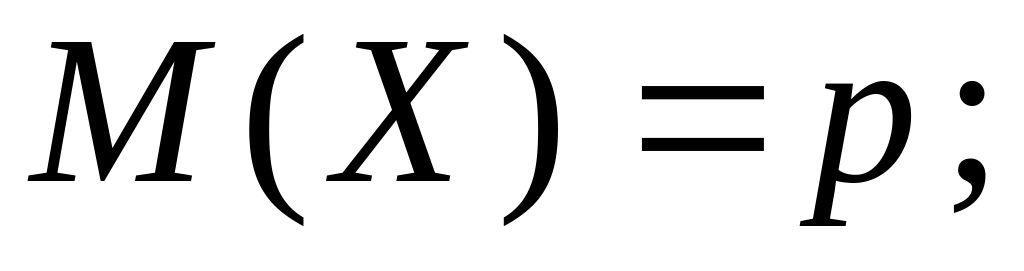
• математичне сподівання числа Х появ події в n випробуваннях за схемою Бернуллі дорівнює добуткові числа n випробувань на ймо­вірність р появи події в одному випробуванні, тобто

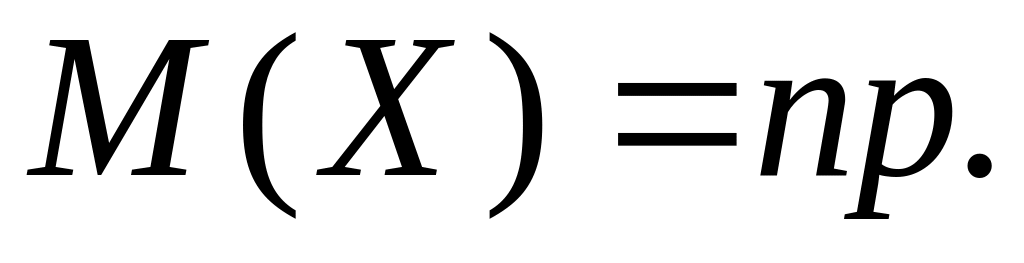
Справді, оскільки випадкова величина Х – число появ події А в одному випробуванні може набути тільки одного з двох значень: з імовірністю і з імовірністю , то

.

Якщо випадкова величина Х – число появ події А в п випробуваннях за схемою Бернуллі, а - число появ події А в одному і-му випробуванні, то

.

За властивістю 3 математичного сподівання

.

Приклад 2.6. Імовірність погашення банківського кредиту кожним клієнтом ста­новить 0,7. Знайти математичне сподівання випадкової величини X – числа клієнтів серед вибраних 10-ти, які своєчасно і в повному обсязі повернуть кредити банкові.

Розв’язання. Оскільки своєчасне погашення кредиту одним клієнтом не залежить від того, чи поверне кредит інший, і ймовірність своєчасного погашення кредиту кожним клієнтом є однакова, то маємо послідовність випробувань за схемою Бернуллі. У даному випадку і тобто в середньому 7 із 10-ти клієнтів погасять кредити своєчасно.

Б. Д и с п е р с і я. Як зазначалося в п. А, математичне сподівання дискретної випадкової величини є точка числової прямої, в околі якої розсіяні її можливі значення. На практиці часто потрібно оцінити це розсіювання. Дане питання вирішується за допомогою дисперсії.

Нехай X – дискретна випадкова величина, закон розподілу якої записано у формі таблиці (табл. 2.1).

Означення. Відхиленням дискретної випадкової величини X від її мате­матичного сподівання називається різниця

Відхилення є також дискретна випадкова величина, яка має такий закон розподілу (табл. 2.5):

Таблиця 2.5

xi – M(X)
р = pi

Зауважимо, що математичне сподівання відхилення Х – М(Х) дорівнює нулю:

З останньої рівності випливає, що середнє значення розсіювання випадкової величини X в околі її математичного сподівання неможливо характеризувати за допомогою зваженої суми відхилень , бо ці різниці мають різні знаки і в сумі вони взаємно анулюються. У такому разі можна було б узяти зважену суму абсолютних значень цих різниць . Однак на практиці середнє значення розсіювання значень випадкової величини Х в околі її математичного сподівання М(Х) частіше оцінюють за допомогою величини [X – M(X)]², яка має такий закон розподілу (табл. 2.6):

Таблиця 2.6

[Х – M(X)]2 = [xi – M(X)]2
р = pi

Означення. Дисперсією дискретної випадкової величини X називається математичне сподівання квадрата відхилення цієї величини від її математичного сподівання, тобто

(2.4)

Використавши властивості математичного сподівання, формулу (2.4) можна звести до вигляду:

.

Формулу одержимо з формули , перетворивши її праву частину:

.

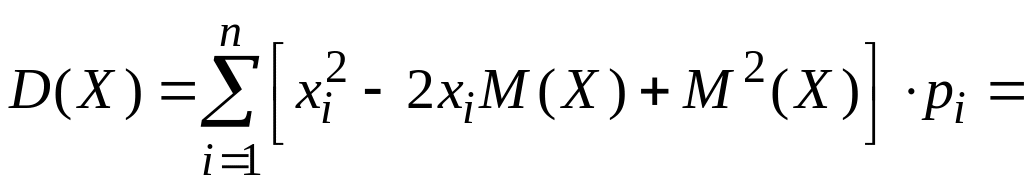
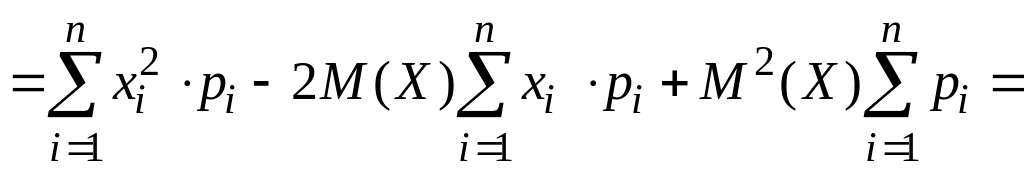
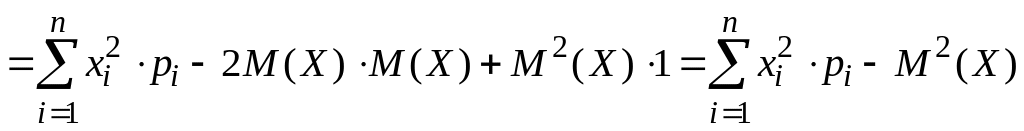Із формули випливає, що дисперсія дискретної випадкової величини дорівнює різниці між математичним сподіванням квадрата цієї величини і квадратом її математичного сподівання.

У випадку, коли множина різних значень дискретної випадкової величини Х є нескінченна і зліченна, то

або

за умови, що числові ряди в правих частинах цих формул є збіжні.

Дисперсія має такі властивості:

1. Дисперсія сталої величини дорівнює нулю, тобто якщо то

Дійсно, за означенням дисперсії

.

Оскільки , то

.

2. Сталий множник виноситься у квадраті за знак дисперсії, тобто якщо то .

За формулою (2.4)

.

Враховуючи властивість 2 математичного сподівання одержимо:

.

3. Дисперсія суми двох незалежних випадкових величин (або кількох взаємно незалежних величин) дорівнює сумі дисперсій цих величин: .

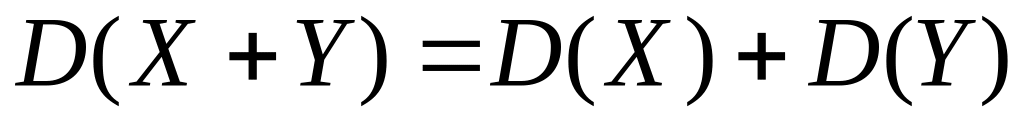Справді, за формулою

.

Врахувавши властивості математичного сподівання, маємо:

.

Зауваження. Дана властивість поширюється на випадок довільного числа випадкових величин: якщо - взаємно незалежні випадкові величини, то

.

3. Дисперсія різниці двох незалежних випадкових величин дорівнює сумі дисперсій цих величин: .

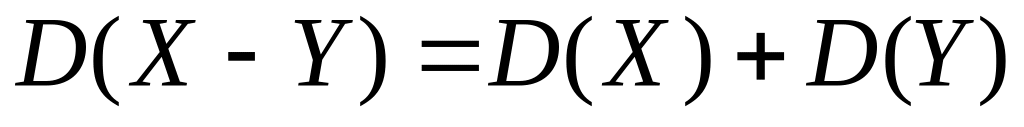Цю властивість обгрунтуємо, використавши властивості 2 і 3 дисперсії:

Зокрема, якщо С – стала величина, то .

Зауваження. У разі проведення послідовності n експериментів (випро­бувань) за схемою Бернуллі дисперсія випадкової величини Х – числа появ події А в цих випробуваннях обчислюється за формулою:

де р = const – імовірність появи події А в окремому експерименті, q = 1 – p.

Наведена формула для обчислення дисперсії випливає з таких міркувань. Якщо Х – число появ події А в серії з п випробувань за схемою Бернуллі і - число появ цієї події в і-му випробуванні , то

.

Величини - взаємно незалежні, тому відповідно із зауваженням до властивості 3 дисперсії маємо:

.

Математичне сподівання числа появ події А в одномі випробуванні дорівнює ймовірності р появи цієї події: .

Випадкова величина може набувати тільки двох значень: з імовірністю р і з імовірністю . Тому

.

Звіси випливає, що

.

У результаті

.

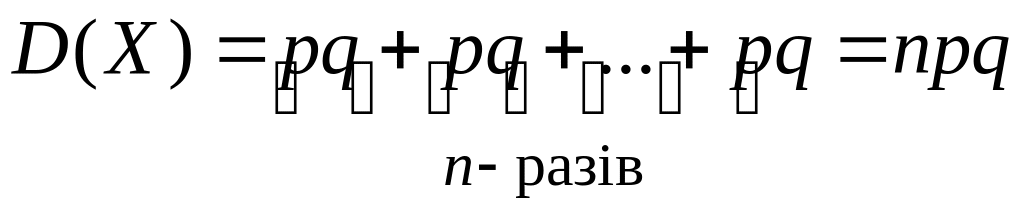В. С е р е д н є к в а д р а т и ч н е в і д х и л е н н я. Викорис­товуючи дисперсію для характеристики розсіювання випадкової величини, стикаємося з однією незручністю: якщо випадкова величина вимірюється в деяких одиницях, то дисперсія вимірюватиметься у квадратах цих одиниць. Тому доцільно мати характеристику розсіювання значень випадкової величини тієї ж вимірності, що й сама величина. Такою характеристикою є середнє квадратичне відхилення.

Означення. Середнім квадратичним відхиленням дискретної випадкової величини X називають корінь квадратний із дисперсії і позначають тобто

(2.5)

Відзначимо основну властивість середнього квадратичного відхилення: якщо , де – взаємно незалежні ви­падкові величини, то

Дана рівність випливає безпосередньо з означення середнього квадратичного відхилення і властивостей дисперсії. За властивістю дисперсії

,

Оскільки , то остаточно маємо, що

Приклад 2.7. Кожна з чотирьох електролампочок має дефект із імовірністю ( – імовірність того, що лампочка дефекту не має). Послідовно беруть по одній лампочці, угвинчують у патрон і вмикають електричний струм. Якщо під час увімкнення струму лампочка перегорить, то вгвинчують наступну. Написати закон розподілу випадкової величини X – числа лампочок, які будуть випробувані, та обчислити і

Розв’язання. Описана в задачі дискретна випадкова величина X набуває можливих значень: Імовірності подій , і = 1, 2, 3 обчислюємо за формулою (2.2):

Для обчислення ймовірності події Х = 4 використовуємо той факт, що ця подія є сумою двох несумісних подій: – під час послідовного випробування 4-х лампочок три з них перегорять, а четверта не перегорить; – під час послідовного випробування 4-х лампочок усі вони перегорять. Тому

Отже, закон розподілу випадкової величини Х має вигляд:

Х = xi	1	2	3	4
р = pi	0,9	0,09	0,009	0,001

Далі обчислюємо:

=

Г. М о д а і м е д і а н а.

Означення. Модою дискретної випадкової величини Х називається те її значення , ймовірність набуття якого є найбільшою.

Означення. Медіаною дискретної випадкової величини Х називається те її значення у законі розподілу, для якого сума ймовірностей можливих значень зліва і справа від нього не перевищує 0,5.

Математичне сподівання, мода, медіана та дисперсія характеризують найбільш важливі риси розподілу випадкової величини, а саме, відповідно його центральну тенденцію та ступінь розсіювання можливих значень величини навколо середнього значення. Крім цих характеристик, у теорії ймовірностей застосовуються деякі інші чисельні характеристики відповід­ного призначення, кожна з яких характеризує випадкову величину з позиції тих чи інших особливостей її розподілу.

Д. П о ч а т к о в і і ц е н т р а л ь н і м о м е н т и.

Означення. Початковим моментом s-го порядку дискретної випадкової ве­личини називають математичне сподівання величини і позначають :

. (2.6)

Якщо закон розподілу випадкової величини Х задається табл. 2.1, то

,

бо можливими значеннями випадкової величини є , а ймовірності їх набуття дорівнюють відповідно.

Зокрема, , , і для обчислення дисперсії маємо таку формулу:

.

Означення. Центральним моментом s-го порядку дискретної випадкової величини X називається математичне сподівання величини і позначається :

(2.7)

Якщо закон розподілу випадкової величини Х задано табл. 2.1, то

бо можливими значеннями випадкової величини є , а ймовірності набуття цих значень дорівнюють відповідно. Зокрема, .

Приклад 2.8. обчислити початковий і центральний моменти 3-го порядку за даним законом розподілу ймовірностей дискретної випадкової величини Х, що пред­ставлений у формі таблиці:

Х = хі	–8	–4	–1	1	4	8
р = рі	0,1	0,2	0,2	0,2	0,2	0,1

Розв’язання. За формулою (2.6), маємо:

За формулою (2.7) і, враховуючи, що М(Х) = 0, маємо:

Між центральними і початковими моментами існує зв’язок: одні вира­жаються через інші. Зокрема, виконується рівність

яка випливає з таких обчислень:

Аналогічно доводимо, що

Справді, користуючись формулою для куба різниці, знайдемо:

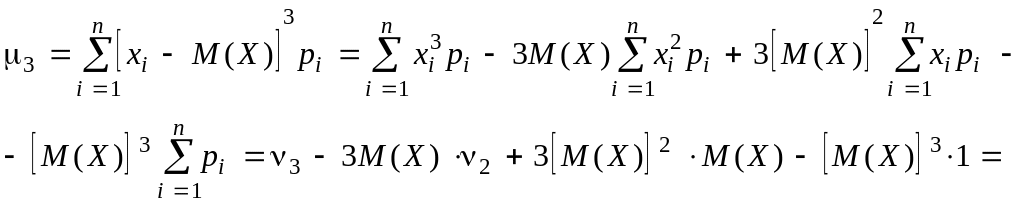
Зауважимо, що третій центральний момент використовується для характеристики асиметрії розподілу. Якщо розподіл симетричний відносно математичного сподівання, то всі центральні моменти непарного порядку (якщо вони існують) дорівнюють нулю. Тому природно за характеристику асиметрії обрати який-небудь із непарних центральних моментів – найпрос­тіше . Але незручність використання полягає в тому, що його вимірність є кубом розмірності випадкової величини. Щоб усунути цю незручність, за характеристику асиметрії обирають безвимірну характе­ристику – відношення третього центрального моменту до куба середнього квадратичного відхилення, яке називають коефіцієнтом асиметрії, або просто асиметрією.

Е. А с и м е т р і я і е к с ц е с.

Означення. Асиметрією дискретної випадкової величини Х називається число , яке обчислюється за формулою:

. (2.8)

Для симетричного розподілу А = 0. Якщо A > 0 (А < 0), то маємо розподіл із правосторонньою (лівосторонньою) асиметрією.

Четвертий центральний момент використовується для характеристики ступеня концентрації можливих значень випадкової величини Х навколо центру розподілу, або, іншими словами, для характеристики гостро­вершинності чи плосковершинності розподілу (застосовується зазвичай для характеристики неперервних випадкових величин). Ця властивість харак­теризується за допомогою так званого ексцесу.

Означення. Ексцесом дискретної випадкової величини Х називається число , яке обчислюється за формулою:

. (2.9)

Число 3 віднімається від відношення тому, що для найбільш поширеного нормального розподілу (про нього буде мова в пункті 2 цього розділу) відношення = 3; криві або ймовірнісні многокутники розподілу, які є більш гостровершинні, ніж нормальний, мають додатний ексцес, а більш плосковершинні – від’ємний ексцес. Чисельною характеристикою Е ко­ристуються здебільшого для симетричних або близьких до нього розподілів.