Залежи с подошвенной водой

Теория конусообразования Маскета-Чарного допускает использование уравнений (13.4.4) и (13.4.5) при возмущенных первоначальных границах раздела ВНК и ГНК. Используя методику определения предельных безводных и безгазовых дебитов для вертикальной скважины, дренирующей нефтегазовую залежь с подошвенной водой и верхним газом (см. §11.3.4), и уравнения (13.4.4) и (13.4.5) можно получить строгое решение аналогичной задачи для горизонтального ствола.

Возьмем производные по ординате ξ потенциалы (13.4.4) и (13.4.5):

(13.4.6)

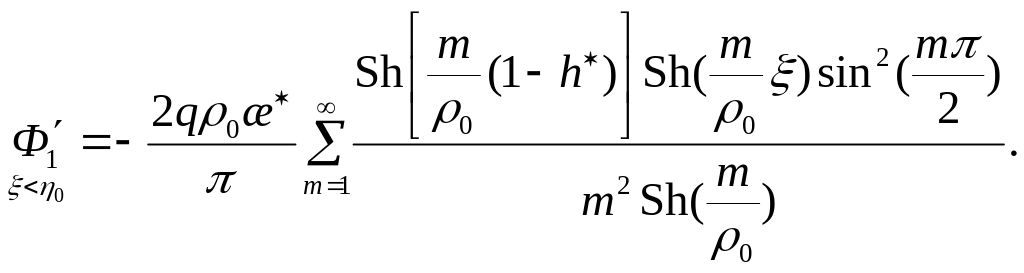(13.4.7)

Линию, проходящую через точечный сток (см. рис. 13.8) параллельно кровле и подошве можно принять за непоницаемую перегородку. Таким образом формально получаем два пласта с толщинами h₁ и h₂. При дренировании верхнего пласта h₁ образуется конус газа, а для нижнего пласта h₂ – конус воды.

Чтобы определить предельные безводные и безгазовые дебиты, необходимо знать ординаты вершин конусов в их предельно-устойчивом состоянии. Сделать можно следующими способами:

– обозначая сумму ряда в уравнении (13.4.4) через и строя графическое ее изображение как функции при фиксированных параметрах , методом касательной определить ординату (см.рис.11.9);

– строя графические изображения функции и ее производной , формула (13.4.7), от ординаты , по точке их пересечения находим ;

– приравнивая и и задавая различные значения , методом итерации (на ПК) определяется значение

В соответствии с теорией конусообразования Маскета-Чарного потенциал вдоль устойчивой границы раздела двух жидкостей (профиль конуса) изменяется по линейному закону. Для нашего расчетного блока имеем [2,7]:

(13.4.8)

Решая совместно (13.4.4) и (13.4.8) при получаем формулу для безразмерного удельного расхода:

(13.4.9)

Для определения ординаты верхнего пласта выполняется аналогичная процедура. Тогда безразмерный удельный дебит λ₁ рассчитывается по формуле (13.4.9) с заменой на и на ; минимальный из этих дебитов λ=min[λ₁, λ₂] принимается как одновременно предельный безводный и безгазовый.

Исследование рядов (13.4.1) и (13.4.2) на сходимость дано в работе [4,7] и иллюстрируется табл.13.3 (Δ – есть отношение остаточного члена ряда к сумме предыдущих).

Как видим, степень погрешности формул (13.4.1) и (13.4.2) зависит от параметра ρ_о и числа принятых членов m в бесконечных рядах. Так при (сильно анизотропные пласты) при m=1 погрешность составляет не более 0,19 %; при m=4 и ρ₀=10 погрешность Δ=8%. Поэтому для практических расчетов в приведенных рядах при 2<ρ₀≤10 достаточно удержать не более m=4 членов.

Таблица 13.3

Погрешность формул (13.4.1) и (13.4.2)

m	Ρ0
	1	2	10
	Δ %
1	0,19	4,30	55
2	0,40.10-3	0,19	28
3	0,19.10-4	0,75.10-2	15
4	-	-	8

Сравнивая ряды в уравнениях (13.4.1) и (13.4.2) с аналогичными рядами в уравнениях потенциалов для вертикальных скважин [7,30], находим почти их полную аналогию. Отличие заключается в выражениях параметра размещения ρ. Исходя из равных объемов дренирования для вертикальной скважины и горизонтального ствола πR h₀=2 _кLh₀ следует выражение для эквивалентного радиуса нашего расчетного блока

(13.4.10)

где

L – длина горизонтального ствола.

Для вертикальной скважины выражение для параметра . Внося (13.4.10) вместо R_к и делая некоторые преобразования, получаем формулу для эквивалентного параметра размещения скважин

(13.4.11)

что дает право использовать полученные результаты для притока к вертикальной скважине применительно к горизонтальному стволу, в особенности, если принять последний как линию стоков. В этом случае в полученных нами уравнениях следует принять .

В соответствии с изложенным за расчетные предельные удельные дебиты принимаем λ₁ и λ₂ для точечного стока [7,8] дренирующего нефтегазовую залежь с круговым контуром питания, табл. 13.4. В этом случае оптимальное положение скважины стока, обеспечивающее одновременно безводный и безгазовый предельный дебит, определяется соотношением[7,8]

(13.4.12)

Расчетные значения функции (13.4.12) приведены в табл. 13.4 и представлены графиками, рис. 13.8.

Таблица 13.4