Результаты расчетов погрешности d0 по формуле (11.49)

Параметры
	1		2	4	8
r0=0,05; =0,8; x0=0,97 r0=1; =0,1; x0=0,60 r0=4; =0,1; x0=0,43 r0=10; =0,1; x0=0,32 r0=100; =0,1; x0=0,26	3 40 57 68 74		1,5 20,0 214.5 34,0 37.0	0,75 10,0 14.3 17,0 18,5	0,38 5,0 7,1 8,5 9.3

Как видно из таблицы для малых значений r₀ и больших значений вскрытия h погрешность формул (11.45) и (11.48) незначительна (первая строка), тогда как с уменьшением вскрытия и увеличением r₀ погрешность растет. Однако при ³8 погрешность формул (11.45) и (11.48), даже для больших значений r₀, не превосходит 10%. Заметим, что в работе [29] оценивается погрешность d<10% при >10.

В работе [29] при определении депрессии исходим из двучленной формулы притока

, (11.50)

где

Q=Q_пр – предельный безводный дебит газовой скважины, который авторами [29] определялся при линейном законе фильтрации.

Здесь мы покажем способ определения ΔР_пр при линейном законе фильтрации (В=0), который не требует определения предельного расхода Q_пр.

Из уравнения (11.50) при В=0 следует

, (11.51)

где

А – коэффициент фильтрационного сопротивления, определяемый как по результатм исследования скважин, так и аналитически (см. §9.2.3)

(11.52)

S=С₁+С₀+С_ск – суммарные добавочные фильтрационные сопротивления, обусловленные соответственно относительным вскрытием пласта, перфорацией колонны и скин-эффектом.

Внося выражение (11.46) в (11.51), получаем

(11.53)

Произведение параметров АQ₀ в соответствии с формулами (11.52) и (11.41) составит:

. (11.54)

Вводя безразмерные параметры

(11.55)

и внося (11.54) в (11.53), после ряда преобразований находим выражение для безразмерной депрессии

(11.56)

где

(11.57)

Размерная депрессия определится из соотношения (11.55): .

Таким образом, для определения ΔР_пр необходимо знать средневзвешенное пластовое давление Р₀, плотности ρ_в и ρ_г, геометрию пласта, безразмерный предельный дебит по жидкости q_ж, а также безразмерную ординату вершины конуса, метод определения которых изложен в § 11.2.2.

11.5. Решение задач конусообразования по двухзонной схеме притока

11.5.1. Расчет предельных дебитов несовершенных скважин и депрессий в однородно-анизотропном круговом пласте с подошвенной водой в случае притока вязкопластичной нефти. Методика расчета предельных безводных дебитов для притока неньютонговских нефтей остается такой же, как и для обычных вязких нефтей. Принимая двухзонную схему притока нефти с подошвенной водой (см. рис. 11.2), записывается условие устойчивости для двух точек поверхности раздела жидкостей и вводя коэффициент структурномеханической вязкости нефти η(τ₀) и ординату вершины устойчивого конуса воды, получаем

. (11.5.1)

Используя решение IX (47) и IX (48') [12] для притока вязкопластичной нефти к несовершенной скважине, при r=0 получаем [12]:

, (11.5.2)

где

. (11.5.3)

Здесь функция определяется рядом IX (48’) [12] при =0.

Предельный безразмерный безводный дебит находится из совместного решения уравнений (11.5.2) и (11.5.3) при x=x₀ по формуле:

, (11.5.4)

где

; (11.5.5)

. (11.5.6)

Значение ординаты x₀ можно определить графическим путем из уравнения (11.5.3) или из совместного решения уравнения (11.5.3) и его производной по параметру .

Заметим, формула (11.5.4) имеет такой же вид, как и формула для притока нъютоновской жидкости, только вместо функции фигурирует формула , определяемая по уравнению (11.5.3).

Изложим методику определения предельного безводного дебита. Пусть заданы следующие параметры пласта: ; 8 – отношения радиуса контура питания к начальной толщине пласта; æ^*=0,25; 2,5 – коэффициенты анизотропии; =0,1; 0,8 – относительные вскрытия пласта. Требуется рассчитать предельные безводные дебиты для случаев притока нъютоновской и ненъютоновской нефти.

Находим следующие безразмерные параметры:

.

При .

При .

Здесь  — радиус внутренней зоны, равный =h (см. рис. 11.2).

Для вязко-пластичной жидкости расчеты будем производить по формулам (11.5.2) и (11.5.3) с использованием табл. 11.1 для определения функции . Для фиксированных значений и задаваемых значений x по формуле (11.5.3) находим значения функции и строим зависимость от (рис.11.9).. Значение функции и ординаты x₀, соответствующие предельно-устойчивому положению конуса, находим графическим путем, т. е. методом касательной (рис. 11.9). Предельные значения дебита подсчитываем затем по формуле (11.5.4). Для сравнения рассчитывались значения предельных дебитов в случае притока нъютоновской жидкости и обычных вязких в равных условиях [12]. При этом дебиты определялись по графикам (см. рис. 11.3).

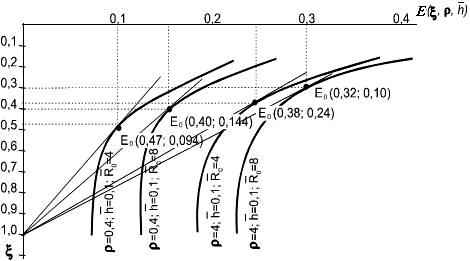
Рис. 11.9. Графическое решение уравнения (11.5.3).