
- •Казунина г.А. , Пинчина л.В. Элементы математической статистики с применением Excel [электронный ресурс]: учеб. Пособие, КузГту.- 2009
- •Д.М. Левин, д. Стефан, т.С. Кребиль, м.Л. Беренсон. Статистика для менеджеров с использованием Microsoft Excel/ Москва, Санкт-Петербург, Киев, “Вильямс”, 2005, 1310 с.
- •Интервальные оценки ( доверительные интервалы) параметров распределения ( стр.230-234)
- •Проверка гипотезы о виде распределения генеральной совокупности
- •Нормальный закон распределения
- •Лабораторная работа № 2.
- •Выборочный коэффициент корреляции служит оценкой коэффициента корреляции и определяется выражением
- •2. Нахождение параметров уравнения линейной регрессии по методу наименьших квадратов
- •По заданной ковариационной функции стационарного случайного процесса найти
- •Принцип максимума л.С. Понтрягина
- •Шаг 4. Находим фазовые траектории при различных возможных значениях управления.
- •Исключая время, получаем уравнение для нахождения фазовой траектории
- •Вопросы к экзамену.
По заданной ковариационной функции стационарного случайного процесса найти
а)
спектральную плотность
![]() :
:
![]()
б)
время корреляции (эффективную длительность
автокорреляционной функции)
![]()
![]() ,
,
с)
эффективную ширину спектра
![]() :
:
![]()
д) среднюю мощность случайного процесса
![]()
ВАРИАНТЫ
1)
![]() ,
2)
,
2)
![]()
3)
![]() 4)
4)
![]()
По заданной спектральной плотности стационарного случайного процесса
 найдите:
найдите:
а)
автоковариационную функцию
![]()
б) дисперсию
с) эффективную ширину спектра:
На вход линейной динамической системы подается случайный сигнал, заданный спектральной плотностью или автоковариационной функцией. Найдите характеристики сигнала на выходе системы:
 ,
,
 ,
среднюю мощность случайного процесса.
Сравните
дисперсии
( средние мощности ) на входе и выходе
системы:
,
среднюю мощность случайного процесса.
Сравните
дисперсии
( средние мощности ) на входе и выходе
системы:
 и
и
 ,
сравните эффективную ширину спектра
и эффективное время корреляции на входе
и выходе системы. При решении задачи
используйте связь между спектральной
плотностью на входе и выходе системы:
,
сравните эффективную ширину спектра
и эффективное время корреляции на входе
и выходе системы. При решении задачи
используйте связь между спектральной
плотностью на входе и выходе системы:
![]()
![]()
ВАРИАНТЫ (выбрать одно уравнение и один вид входного сигнала по указанию преподавателя)
Дифференциальные уравнения линейных систем:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
Возможные входные сигналы:
а) белый шум,
б) низкочастотный белый шум
![]()
![]() и
и
![]() ,
,
с) сигнал с автоковариационной функцией
![]() ,
,
д) сигнал с автоковариационной функцией
РГР 6. Линейные дифференциальные уравнения. Качественная теория. Фазовые портреты.
Литература
Алексеев Д.В., Казунина Г.А. Дифференциальные уравнения с элементами теории устойчивости: учеб. пособ.[электронный ресурс].- КузГТУ.- Кемерово.- 2010
Демидович Б.П. Лекции по математической теории устойчивости [электронный ресурс]: СПб.- Лань, 2008
ВАРИАНТЫ
1.Построить фазовые портреты для автономных дифференциальных уравнений первого порядка. Разбить уравнения на классы качественно эквивалентных и для каждого класса схематично построить интегральные кривые:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)![]() 8)
8)
![]() 9)
9)
![]()
10)
![]() 11)
11)
![]()
12)![]() 13)
13)
![]()
2.а) Преобразовать линейные дифференциальные уравнения второго порядка в равносильную систему линейных уравнений и записать в матричной форме,
б) Найдите собственные значения матрицы системы и определите по ним жорданову форму матрицы и тип фазового портрета,
в) Найдите точные уравнения фазовых траекторий и схематично постройте их,
с) Сделайте вывод об устойчивости нулевого решения.
ВАРИАНТЫ
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
РГР 6. Решение систем линейных дифференциальных уравнений методом матричной экспоненты
Литература
Алексеев Д.В., Казунина Г.А. Дифференциальные уравнения с элементами теории устойчивости: учеб. пособ.[электронный ресурс].- КузГТУ.- Кемерово.- 2010
Демидович Б.П. Лекции по математической теории устойчивости [электронный ресурс]: СПб.- Лань, 2008
3.Решите однородные системы линейных дифференциальных уравнений второго порядка различными методами
а)
с использованием матричной экспоненты
![]()
б)
операторным методом. Начальные условия
заданы в момент
![]()
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
РГР 6. Линейные дифференциальные уравнения.
Решение систем линейных неоднородных уравнений методом матричной экспоненты
Литература
Алексеев Д.В., Казунина Г.А. Дифференциальные уравнения с элементами теории устойчивости: учеб. пособ.[электронный ресурс].- КузГТУ.- Кемерово.- 2010
Демидович Б.П. Лекции по математической теории устойчивости [электронный ресурс]: СПб.- Лань, 2008
Решите
неоднородные системы, используя метод
матричной экспоненты:
![]()
ВАРИАНТЫ:
1)![]() 2)
2)
![]()
3)
![]()
РГР 8. Анализ линейных дифференциальных уравнений высших порядков.
Литература
Алексеев Д.В., Казунина Г.А. Дифференциальные уравнения с элементами теории устойчивости: учеб. пособ.[электронный ресурс].- КузГТУ.- Кемерово.- 2010
Демидович Б.П. Лекции по математической теории устойчивости [электронный ресурс]: СПб.- Лань, 2008
а) перепишите дифференциальные уравнения высших порядков в равносильную систему уравнений первого порядка.
б) запишите систему в матричной форме.
в) найдите собственные значения и жорданову форму матрицы системы.
г) установите, из каких элементарных блоков более низких порядков формируется жорданова форма.
ВАРИАНТЫ:
1)
![]() 2)
2)
![]() 3)
3)
![]()
РГР9. Элементы теории устойчивости
Литература
Алексеев Д.В., Казунина Г.А. Дифференциальные уравнения с элементами теории устойчивости: учеб. пособ.[электронный ресурс].- КузГТУ.- Кемерово.- 2010
Демидович Б.П. Лекции по математической теории устойчивости [электронный ресурс]: СПб.- Лань, 2008
Казунина Г.А. и др. Элементы теории функций комплексной переменной: учеб. пособ. – КузГТУ.- 2008 (Последний параграф по критерию Михайлова)
Исследуйте устойчивость нулевого решения для линейных дифференциальных уравнений и систем, используя критерии а) Гурвица
б) Михайлова
с) анализируя знак вещественных частей собственных значений матрицы (если это возможно).
 ,
,
2)
![]() ,
,
3)
![]()
4)
 5)
5) 6)
6)
Исследовать, при каких значениях параметров нулевое решение асимптотически устойчиво

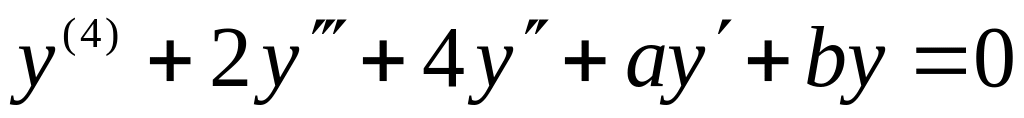

4)
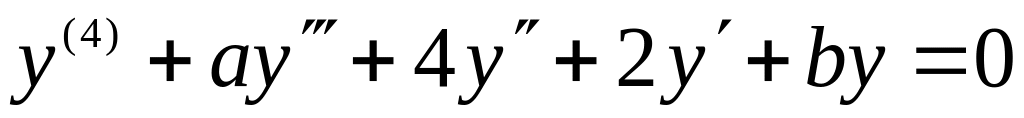
Исследуйте на устойчивость нелинейные системы дифференциальных уравнений:
а) найдите положения равновесия ( неподвижные точки )
б) постройте линеаризованную систему в окрестности каждой неподвижной точки и определите характер неподвижных точек
с) схематично постройте фазовые траектории в окрестности положений равновесия. В том случае, если неподвижная точка является центром, проведите дополнительные исследования.
ВАРИАНТЫ
 2)
2)

3)![]() 4)
4)
![]()
5)
![]() 6)
6)

7)
 8)
8)
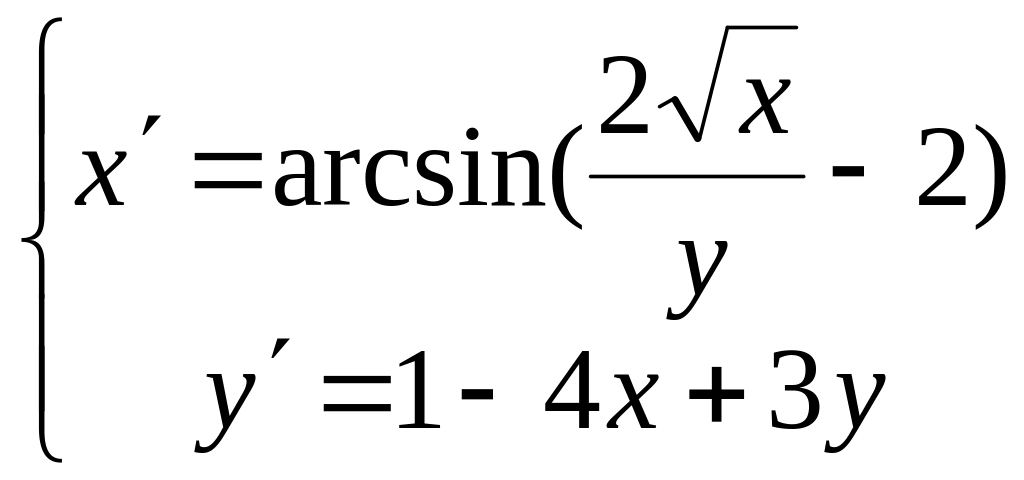
9)
![]() 10)
10)
![]()
11)
 12)
12)

4.Исследовать, при каких значениях параметров нулевое решение системы является устойчивым
ВАРИАНТЫ
 2)
2)

 4)
4)

РГР10. Элементы вариационного исчисления. Экстремали. Принцип максимума Л.С. Понтрягина
Литература
Гюнтер Ф.М. Курс вариационного исчисления [электронный ресурс]
Простейшей вариационной задачей называют задачу нахождения экстремума функционала
![]()
на
множестве непрерывно дифференцируемых
функций
![]() ,
заданных на отрезке
,
заданных на отрезке
![]() и удовлетворяющих условиям
и удовлетворяющих условиям
![]() .
.
Функция, которая доставляет экстремум функционалу, называется экстремалью. Если функция дважды непрерывно дифференцируема на и является экстремалью, то она необходимо удовлетворяет уравнению Эйлера:
![]() .
.
В некоторых случаях решение уравнения Эйлера упрощается по сравнению с общим случаем
Функция
 в
выражении для функционала явно не
зависит от
в
выражении для функционала явно не
зависит от
 :
:
 ( это уравнение не является дифференциальным)
;
( это уравнение не является дифференциальным)
;
Функция
 зависит только от
:
зависит только от
:
 .
Общим решением этого уравнения являются
прямые линии
.
Общим решением этого уравнения являются
прямые линии

Функция
 не
зависит от
не
зависит от
 :
:

Функция явно
 не
зависит от
не
зависит от
 :
:
![]() .
.
ВАРИАНТЫ
1.Найти экстремали функционала, удовлетворяющие заданным граничным условиям.
ВАРИАНТЫ (в скобках указаны ответы)
(![]() )
)
(![]() )
)
(![]() )
)
(![]() )
)
Материальная точка перемещается вдоль плоской кривой
 ,
соединяющей точки
,
соединяющей точки
 и
и
 со
скоростью
со
скоростью
 ,
а точки имеют координаты
,
а точки имеют координаты
(Ответ:
![]() )
)
Задача о брахистохроне. Найдите плоскую кривую, соединяющую точки
 и
и
 , при скатывании вдоль которой под
действием силы тяжести материальная
точка перемещается из
в
за наименьшее время. Ответ:
, при скатывании вдоль которой под
действием силы тяжести материальная
точка перемещается из
в
за наименьшее время. Ответ:

Найти экстремали функционала в задаче с подвижными границами
Простейшая
задача вариационного исчисления с
подвижными границами состоит в определении
функции
![]() и
точек
и
точек
![]() ,
для которых функционал достигает
экстремума при условии
,
для которых функционал достигает
экстремума при условии
![]() .
.
Поскольку в этой задаче значения искомой функции на концах отрезка не зафиксированы, то для определения произвольных постоянных в решении уравнения Эйлера вводятся условия, которые называют условиями трансвесальности:
![]()
![]() .
.
Если на одном из концов искомой функции задано обычное граничное условие, то условие трансверсальности следует записывать только для другого конца.
Если
граничное
условие на одном из концов отсутствует,
,
то это означает, что граничная точка
может
перемещаться по вертикальной прямой и
вместо условия трансверсальности
записывают условие
![]() (
в этой граничной точке).
(
в этой граничной точке).
ВАРИАНТЫ:
(Ответ:
![]() )
)
(Ответ:
![]() )
)
(Ответ:![]() )
)


