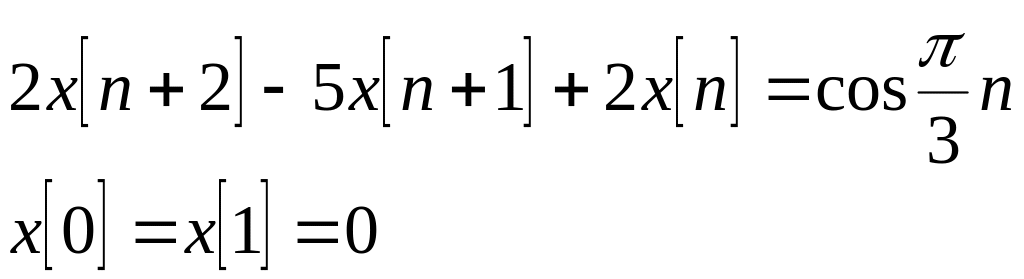Лабораторная работа № 2.

ВЫБОРОЧНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ

Коэффициент корреляции двух случайных величин определяет степень линейной корреляционной зависимости между ними

.

. Если , то случайные величины связаны точной линейной зависимосью.

Выборочный коэффициент корреляции служит оценкой коэффициента корреляции и определяется выражением

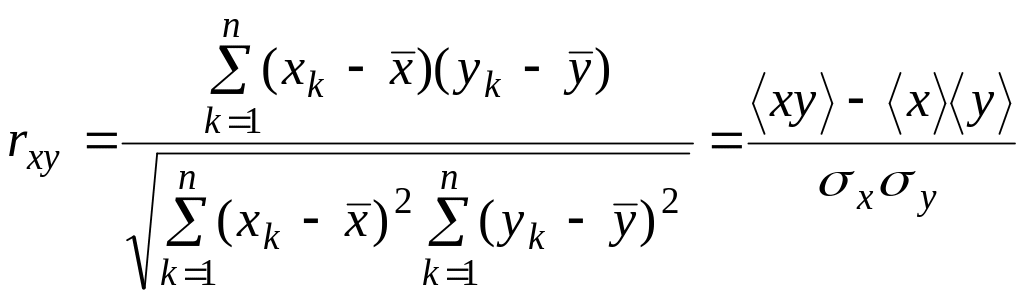, где означает усреднение.

Можно непосредственно вычислять коэффициент по этой формуле, но удобнее выполнять действия по следующему алгоритму (стр. 196-198 или учебное пособие [2] ) .

Полученное при помощи средств EXCEL значение коэффициента корреляции данных массивов равно . Выбираем

на панели инструментов.

ШАГ 5. Проверяем гипотезу о статистической значимости выборочного коэффициента корреляции (стр. 265-266)

Выдвигаем основную гипотезу : и соответствующую альтернативную гипотезу . На заданном уровне значимости находим теоретическое значение статистики критерия согласно выражению

.

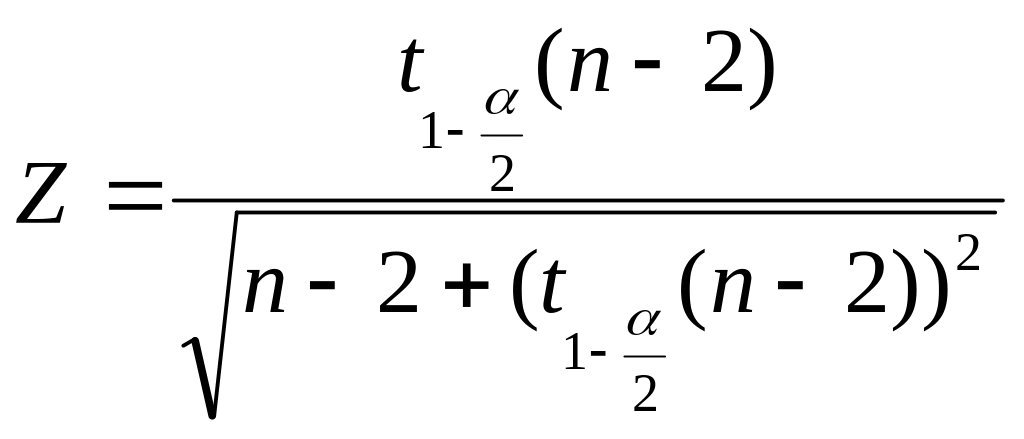Выбрав уровень значимости , находим по таблице (стр. 414) квантиль распределения Стьюдента и вычисляем значение статистики .

Основная гипотеза принимается, если выполняется соотношение и отвергается в случае .

В рассматриваемом случае . Поэтому основная гипотеза отклоняется и принимается гипотеза . Таким образом, коэффициент корреляции на выбранном уровне значимости отличен от нуля. Это свидетельствует о наличии корреляционной зависимости между случайными величинами. Значение коэффициента корреляции близко к единице , что говорит о близости зависимости между случайными величинами к линейной зависимости.

2. Нахождение параметров уравнения линейной регрессии по методу наименьших квадратов

( стр. 291- 298 )

Пусть коэффициент корреляции между двумя случайными величинами значимо отличается от нуля и близок к единице. Предполагаем ( выдвигаем гипотезу ) , что эти случайные величины связаны « в среднем» линейной зависимостью :

РЕГРЕССИЯ – оптимальная зависимость, то есть модель, обеспечивающая аппроксимацию эмпирических данных с наибольшей точностью. Справедливо соотношение

Коэффициенты являются параметрами линейной регрессионной модели. Величина - случайная ошибка наблюдений, причем математическое ожидание

Для нахождения оценок параметров модели используем метод наименьших квадратов. Согласно этому методу в качестве оценок параметров выбирают такие, которые обеспечивают минимум суммы квадратов отклонений наблюдаемых значений случайных величин от их математических ожиданий. Другими словами параметры должны быть такими, чтобы сумма

принимала наименьшее значение. Записываем необходимые условия существования экстремума для функции двух переменных , приравнивая к нулю частные производные

В результате для нахождения оценок получаем систему уравнений:

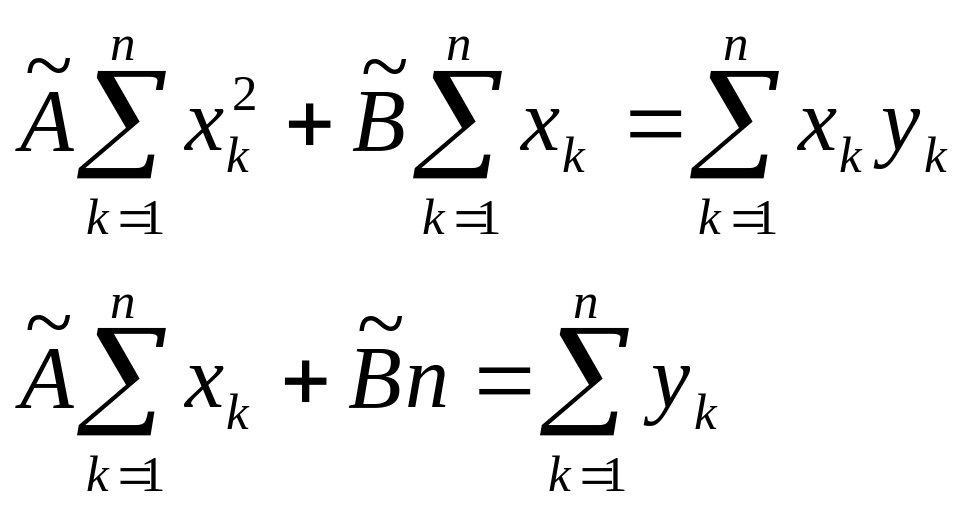
Решение системы имеет вид :

, .

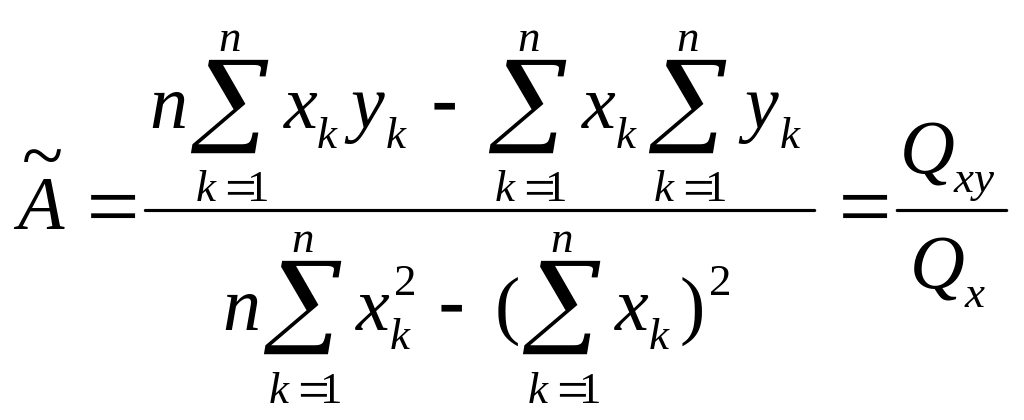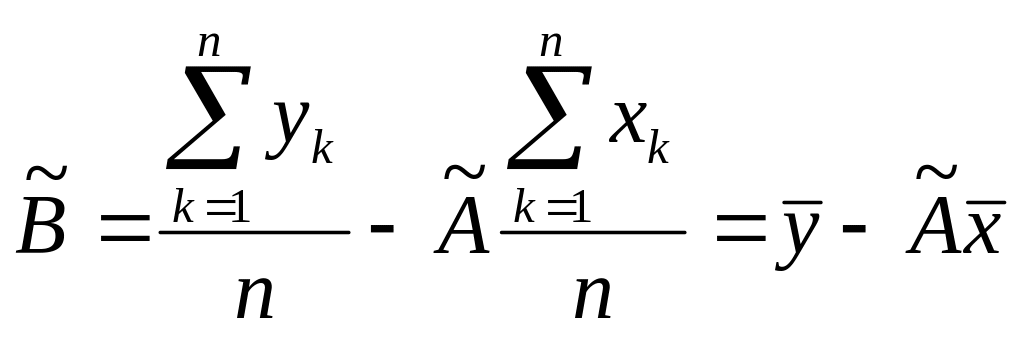Аналогично находим оценки

. При этом .

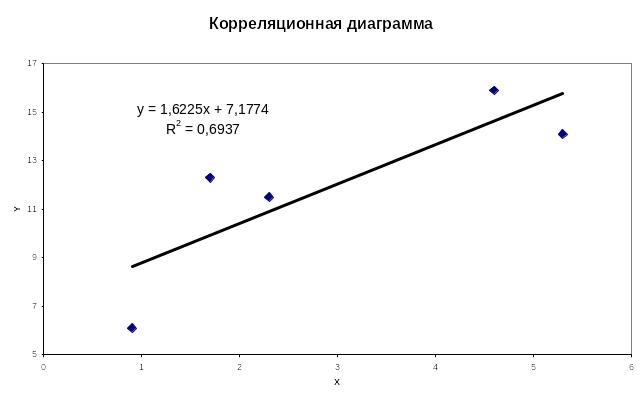
Для рассмотренной задачи

0,9	6,1
1,7	12,3
2,3	11,5
4,6	15,9
5,3	14,1

имеем оценки

И уравнения регрессии имеют вид

Достаточно легко написать программу для получения оценок по методу наименьших квадратов как для линейной , так и для других зависимостей. Но существует много готовых программных средств, решающих эту задачу. Так средства EXCEL позволяют непосредственно получить уравнение линейной регрессии по рядам данных:

Регрессионная модель называется адекватной, если предсказанные по ней значения переменной согласуются с результатами наблюдений. Оценка адекватности может быть проведена следующим образом.

Непосредственный анализ остатков, то есть разностей между наблюдаемыми значениями и вычисленными согласно уравнению регрессии :

.

Если модель адекватна, то остатки, которые являются реализациями случайных ошибок наблюдений, должны быть нормально распределенными случайными величинами с нулевым средним и одинаковыми дисперсиями . Другими словами для случайной величины - остатков – необходимо выполнить лабораторную работу № 1(найти среднее, дисперсию, среднеквадратичное отклонение) и доказать, что на заданном уровне значимости (нулевое значение попадает в доверительный интервал для математического ожидания).

Пример построения прямой регрессии в Excel.

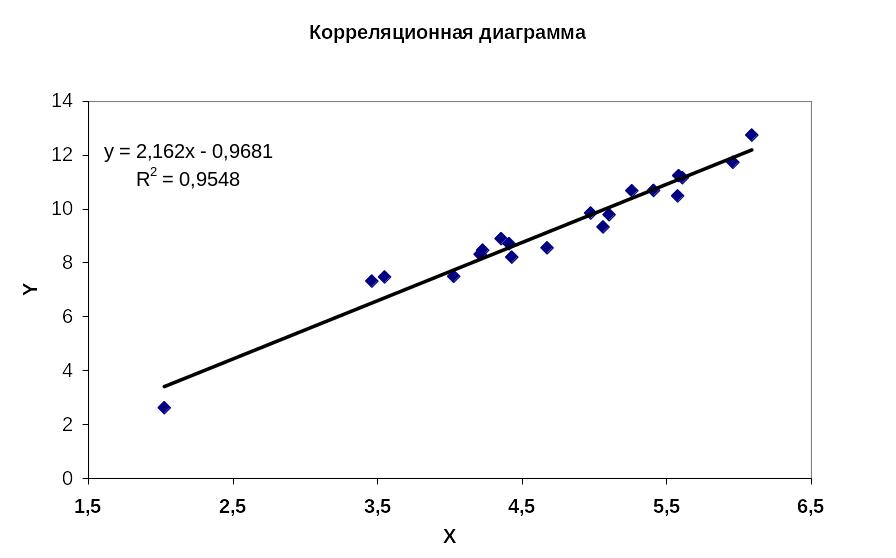
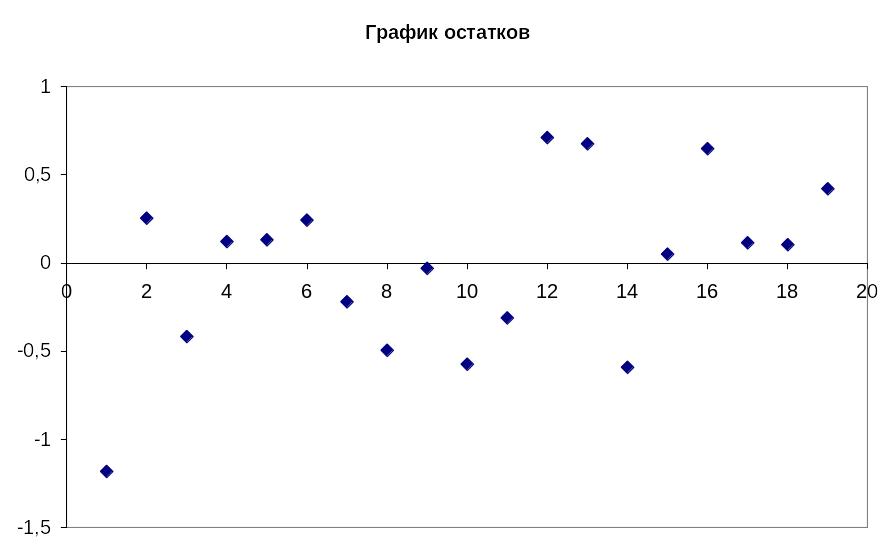
Данные описательной статистики для случайной величины “остатки”

Среднее	6,66134E-16
Стандартная ошибка	0,108822029
Медиана	0,109108445
Мода
Стандартное отклонение	0,486666907
Дисперсия выборки	0,236844679
Эксцесс	0,294111648
Асимметричность	-0,602186657
Интервал	1,892506228
Минимум	-1,181791019
Максимум	0,710715209
Сумма	1,33227E-14
Счет	20
Уровень надежности(95,0%)	0,227767194

Из приведенных зависимостей и расчетов видно, что предложенная регрессионная модель адекватна: остатки распределены около нулевого среднего. Значение стандартной ошибки задает доверительный интервал для , содержащий значение .

Статистическую значимость регрессионной модели можно проверить по коэффициенту регрессиии .

Линейная регрессионная модель называется незначимой, если параметр . Проверку основной гипотезы против альтернативной гипотезы можно провести двумя способами.

СПОСОБ 2 . Находим границы доверительного интервала для параметра :

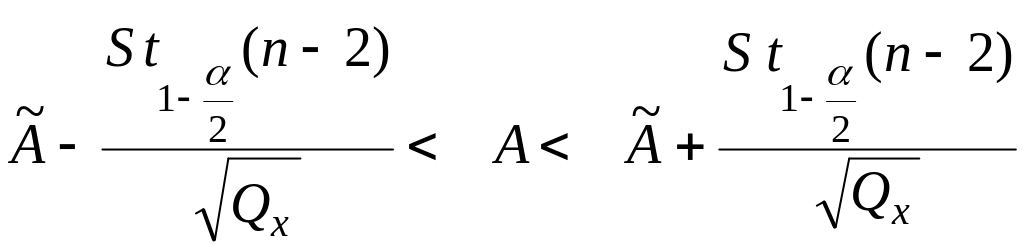
Если для данного уровня значимости доверительный интервал содержит значение , то принимается основная гипотеза и регрессия считается статистически незначимой. В том случае, когда доверительный интервал не содержит нулевое значение параметра, основная гипотеза отклоняется и регрессионная модель считается статистически значимой

Например : или .

Таким образом, на заданном уровне значимости нулевое значение параметра не попадает в доверительный интервал и регрессия признается статистически значимой

Полезной и важной характеристикой линейной регрессии является коэффициент детерминации , который вычисляют по формуле

.

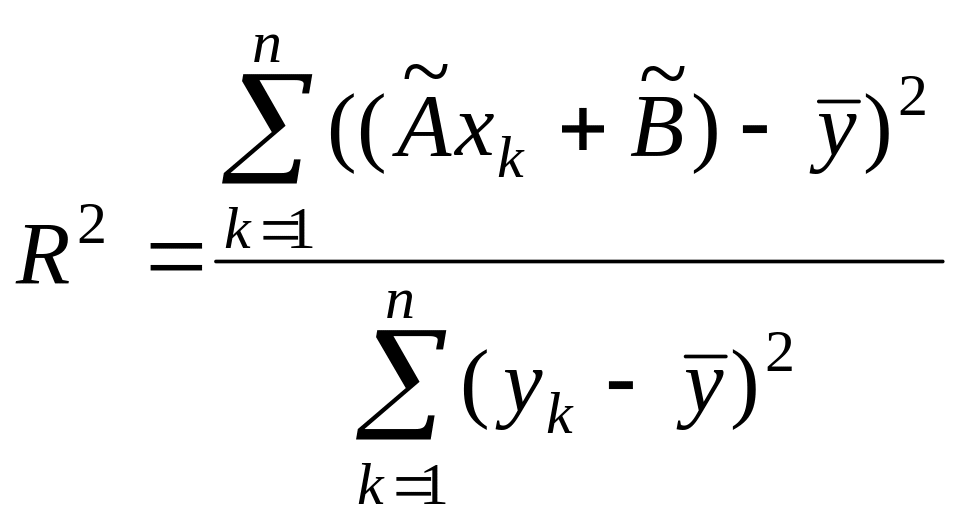Этот коэффициент показывает долю разброса результатов наблюдений около средего значения случайной величины , которую можно объяснить построенной регрессионной моделью , и может быть использован для характеристики не только линейной регрессии, но и для нелинейной. Как видно из определения коэффициента, чем меньше остаточная сумма квадратов , тем ближе значение коэффициента к единице и тем точнее выбранная модель регрессии описывает результаты наблюдений. Значение корня является оценкой коэффициента корреляции между результатами наблюдений и их значениями, вычисленными согласно принятой регрессионной модели. В случае линейной регресссии справедливо . Отметим, что именно значение коэффициента детерминации указывается в EXCEL в качестве характеристики качества аппроксимации.

Ниже приведена выдача из Excel: , для подробного анализа которой следует обратиться к книге [3]. Отметим только, что красным цветом выделен 95% доверительный интервал для коэффициента регрессии : .

	ВЫВОД ИТОГОВ
	Регрессионная статистика
	Множественный R		0,956037
	R-квадрат		0,914006
	Нормированный R-квадрат		0,909229
	Стандартная ошибка		0,500003
	Наблюдения		20
	Дисперсионный анализ
			df	SS		MS		F			Значимость F
	Регрессия		1	47,83		47,83		191,3179			4,96562E-11
	Остаток		18	4,500049		0,250003
	Итого		19	52,33004
			Коэффициенты	Стандартная ошибка		t-статистика		P-Значение			Нижние 95%		Верхние 95%
	Y-пересечение		-0,43605	0,718975		-0,60648		0,5517664			-1,946557679		1,074464255
	Переменная X 1		2,047796	0,14805		13,83177		4,966E-11			1,736753836		2,358837984

РГР 2. Характеристики динамических звеньев

Литература

1. Казунина Г.А. и др. Дискретные и интегральные преобразования: КузГТУ. – 1999

2. Казунина Г.А. Преобразования Фурье. Преобразования Лапласа: учеб. пособие [электронный ресурс].- КузГТУ.- 2009

Для динамических систем, заданных дифференциальными уравнениями, найти следующие характеристики:

1. Передаточную функцию 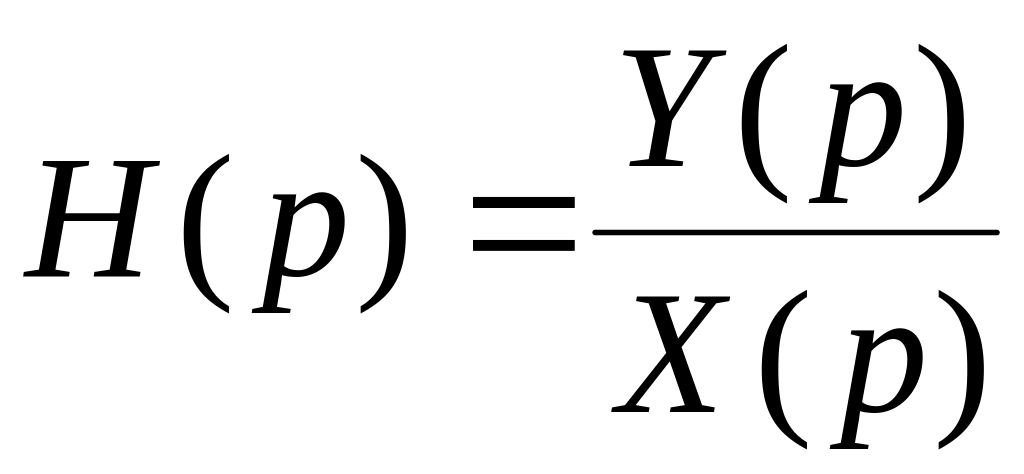- отношение изображения по Лапласу выходного сигнала к изображению входного сигнала при нулевых начальных условиях

2. Импульсную переходную характеристику систем

( реакцию системы на импульсное входное воздействие)

3. Переходную характеристику системы (реакцию системы на ступенчатое воздействие)

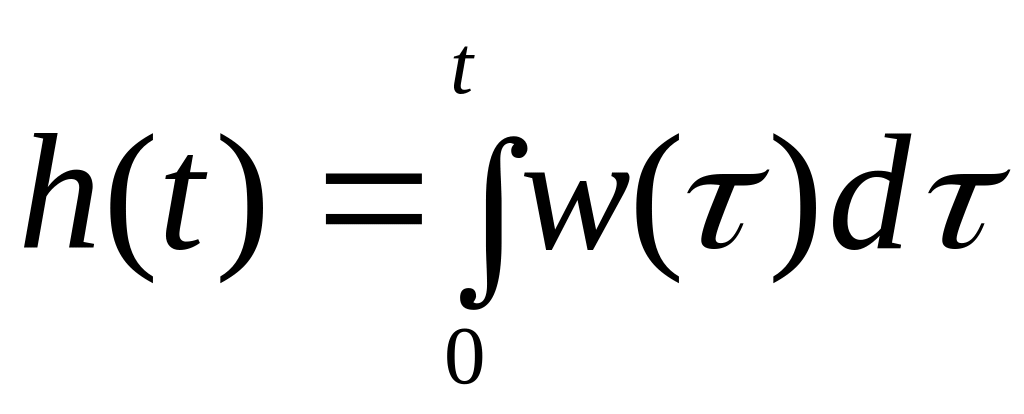
4. Найти реакцию системы на входное воздействие двумя способами а) операторным методом, б) методом свертки

А)

В)

5. Найти частотную передаточную функцию 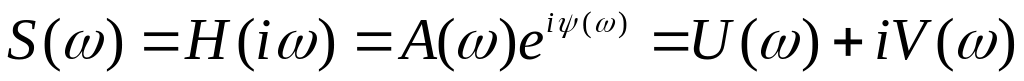, а также

А) амплитудно – частотную характеристику

В) фазово-частотную характеристики

.

С) Постройте графики функций . Примечание: последний график можно построить как функцию параметра ω, используя компьютер.

Пример выполнения задания (вариант 10).

1. Из уравнения 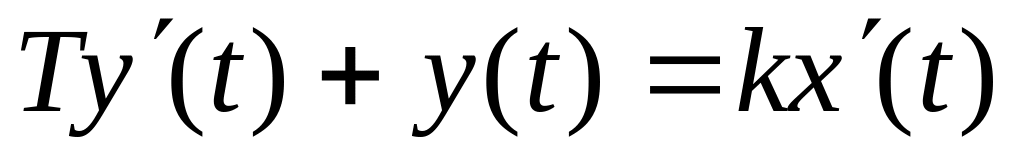, переходя к изображениям Лапласа при нулевых начальных условиях, находим передаточную функцию:

.

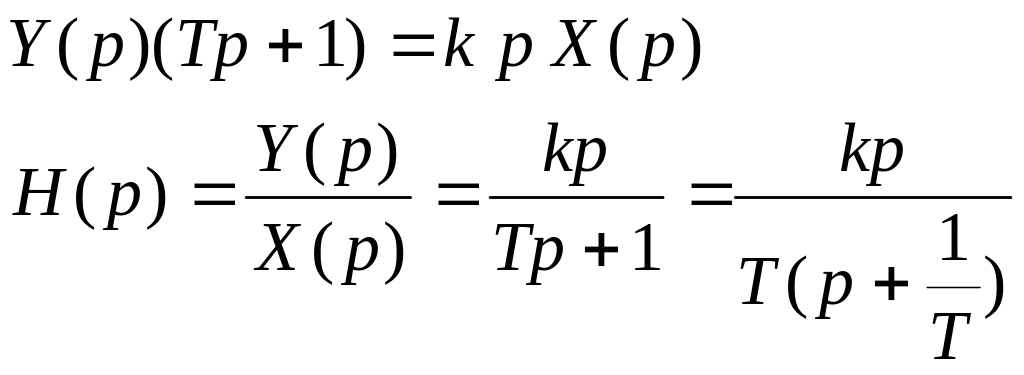2. Поскольку передаточная функция не является правильной дробью, то для перехода к оригиналу выделяем целую часть и остаток

.

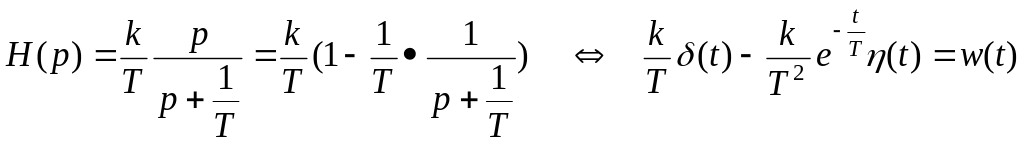3. В результате импульсная переходная характеристика имеет вид

.

Переходную характеристику находим как интеграл от импульсной переходной характеристики:

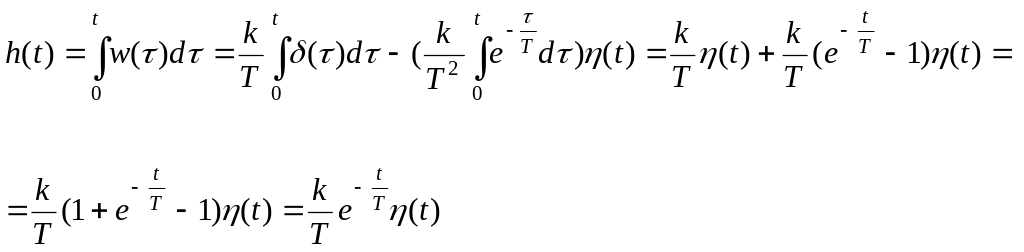
4.Реакцию системы на внешнее воздействие находим двумя способами. Так для сигнала получаем:

Способ 1.

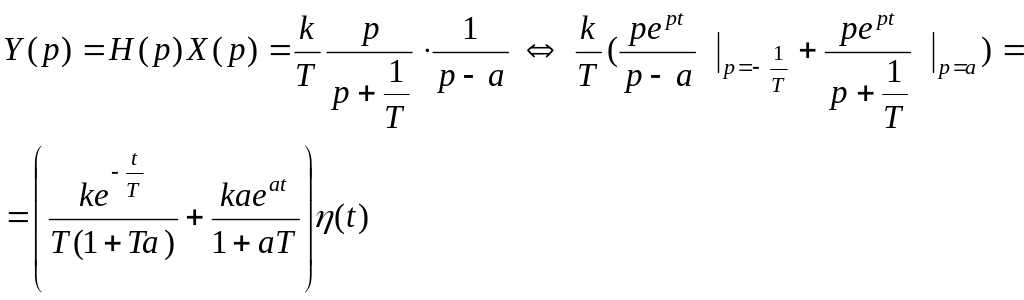Способ 2 Используем формулу свертки с импульсной переходной или переходной характеристикой, например, формулу Дюамеля:

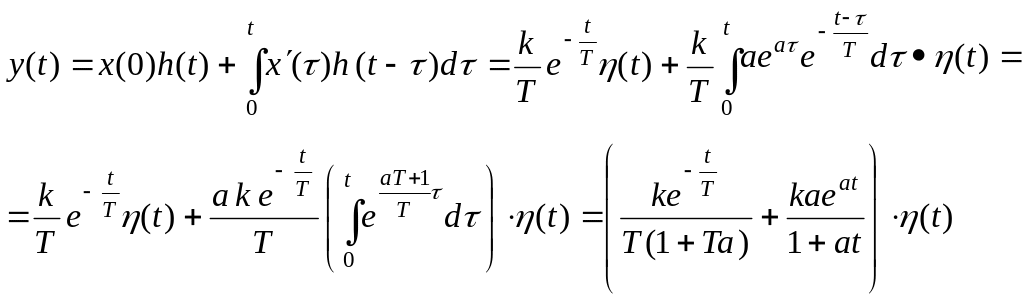
Для входного сигнала получаем:

Способ1.

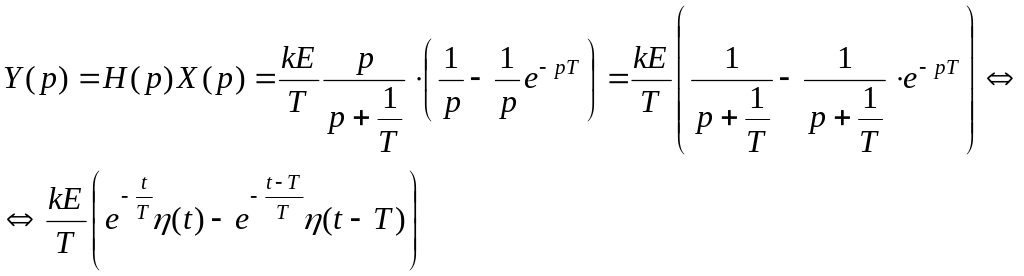
Способ 2.

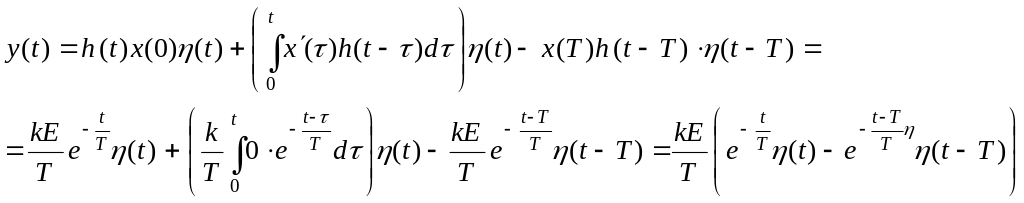
5.Находим частотную переходную характеристику

;

А) Амплитудно-частотная характеристика

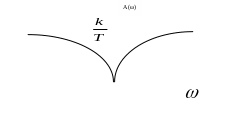
Б) Фазово-частотная характеристика

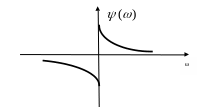
С) Амплитудно-фазовая характеристика строится как кривая в координатах . Кривую можно построить аналитически, исключив параметр ω из системы уравнений:

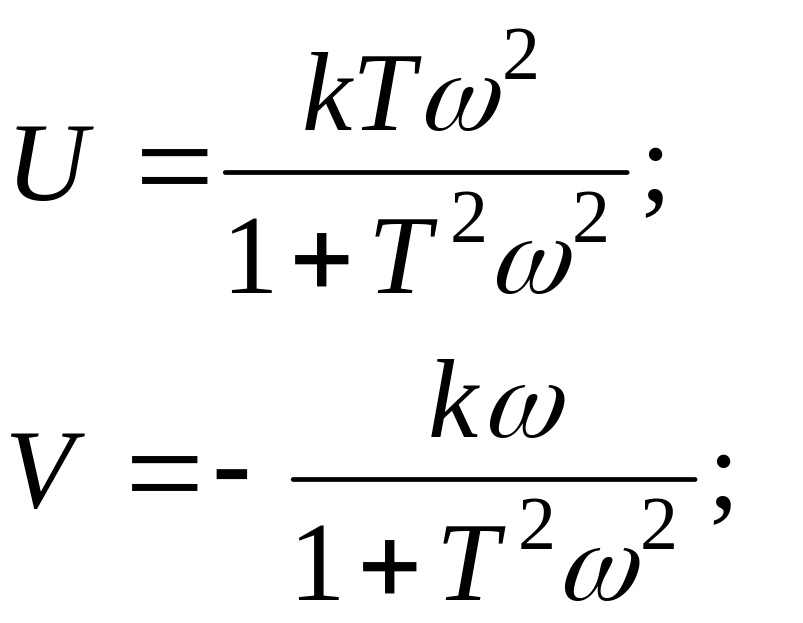
Окончательно получаем смещенную окружность

ВАРИАНТЫ

1) , 2)

3) 4)

5) 6)

7) 8)

9) 10)

РГР 2. Z – преобразования и разностные уравнения

Литература

1. Казунина Г.А. и др. Дискретные и интегральные преобразования: КузГТУ. – 1999

2. Казунина Г.А. Преобразования Фурье. Преобразования Лапласа: учеб. пособие [электронный ресурс].- КузГТУ.- 2009

-преобразованием для числовой (действительной или комплексной) бесконечной последовательности называют функцию комплексной переменной которая определяется как разложения в ряд Лорана в окрестности бесконечно удаленной точки :

Если функция является решетчатой функцией и удовлетворяет условию то ряд Лорана сходится в области то есть вне круга с центром в начале координат и радиусом Функция является в этой области аналитической функцией.

Пример 1. Найти Z-преобразование функции .

Разложение функции в ряд Лорана имеет вид:

Так как данный ряд является геометрической прогрессией со знаменателем и первым членом прогрессии, равным , то сумма ряда равна:

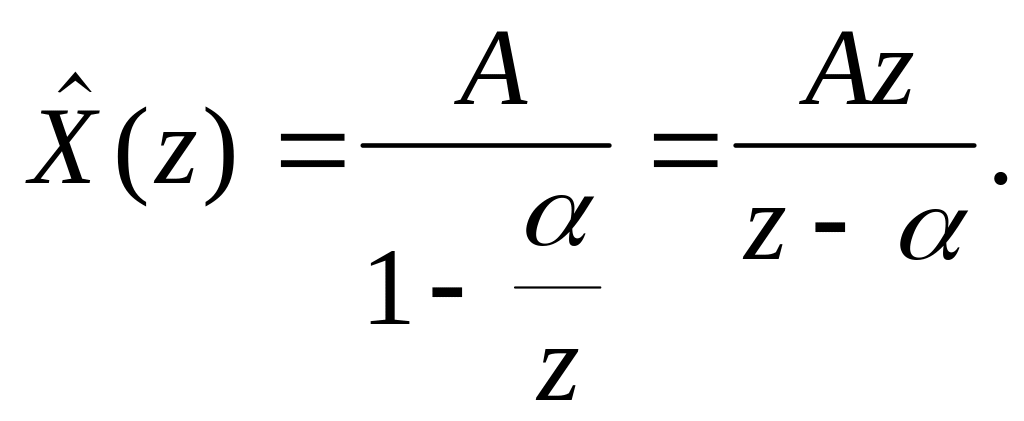
Область сходимости ряда:

В дальнейшем будем обозначать соответствие между решетчатой функцией и ее Z- преобразованием следующим образом:

Пример 2. Найти Z-преобразование для функции

Разложение функции в ряд Лорана имеет вид:

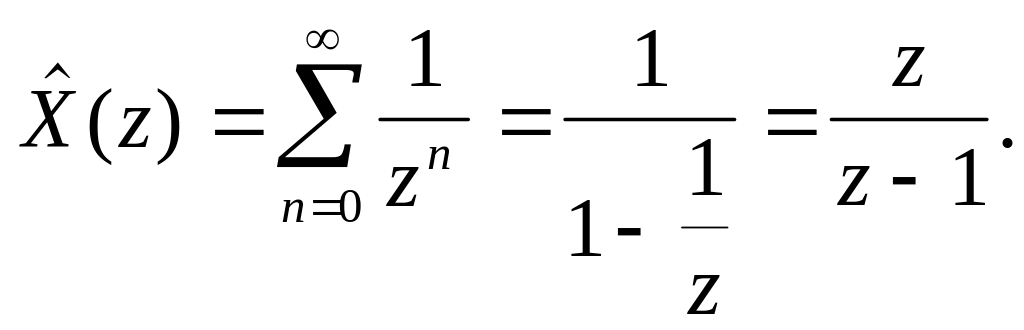
Область сходимости ряда определяется соотношением: или Полную таблицу преобразований найдите в указанной выше литературе.

Восстановить решетчатую функцию-оригинал (общий член последовательности) можно используя общую формулу для коэффициентов ряда Лорана в окрестностях :

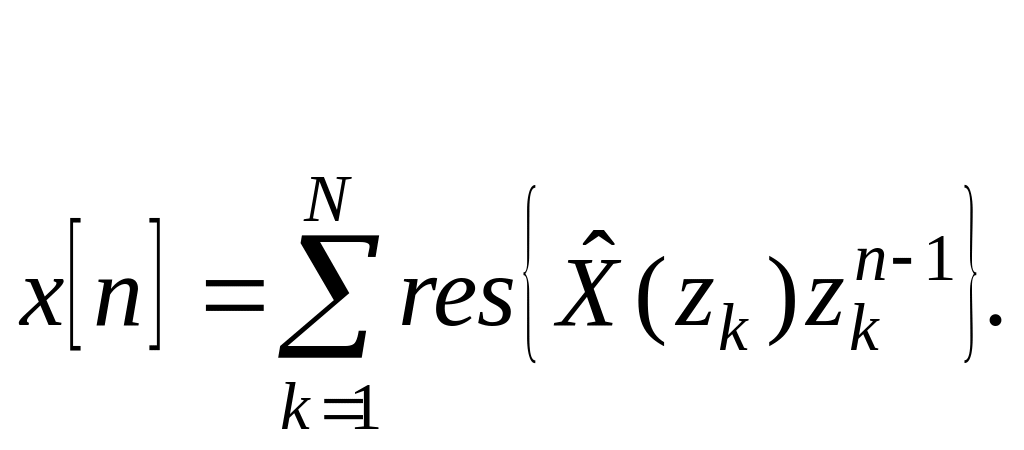
Сумма вычетов берется по всем особым точкам, лежащим в конечной части плоскости.

Пример. Восстановить решетчатую функцию

Функцию x[n] восстанавим по формуле для коэффициентов ряда Лорана:

С учетом того, что данная функция имеет простые полюсы в точках z = 2 и z = 3, получаем:

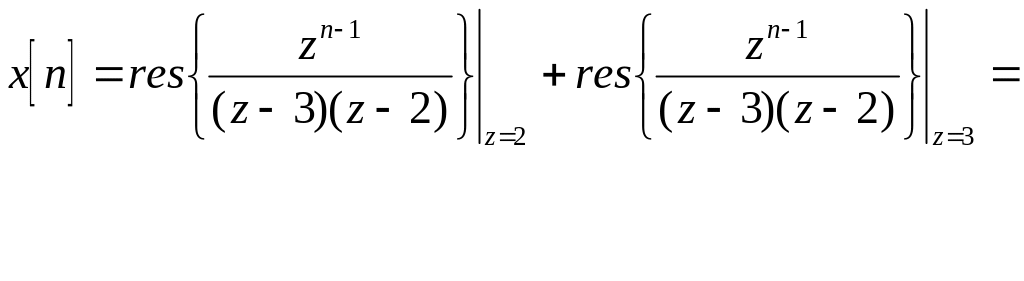
Некоторые свойства преобразований:

1. ,

2. 

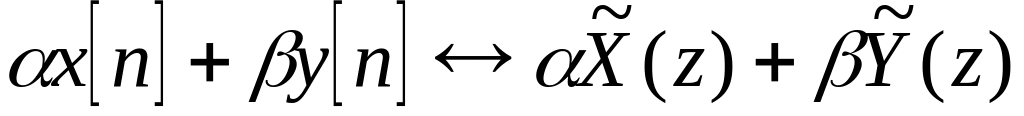ВАРИАНТЫ

Решите линейные разностные уравнения и системы уравнений:

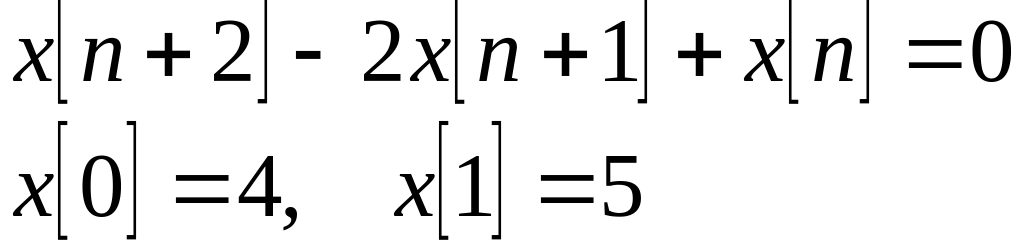1. Ответ:

2)

Ответ: .

3. 

Ответ:

3. Ответ: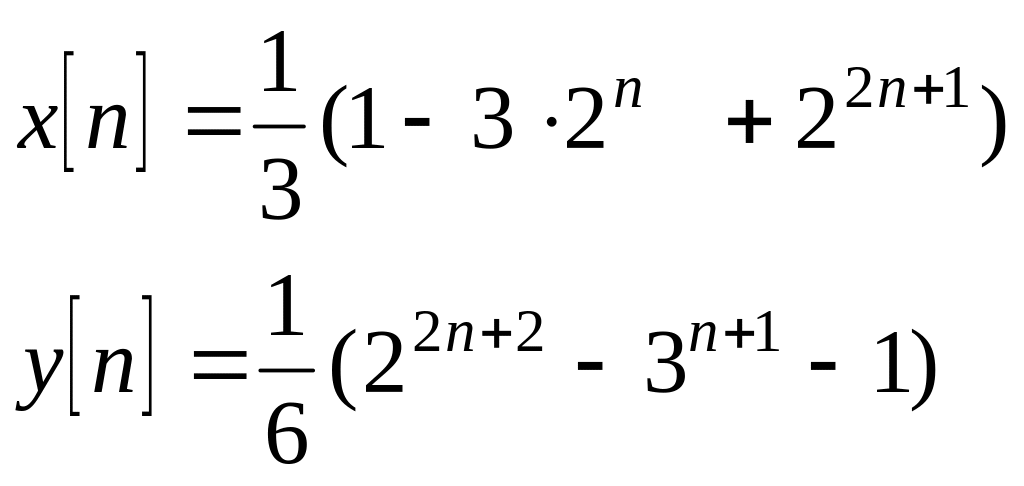

РГР4. Случайные процессы. Корреляционная теория.

Литература.

1. Сборник задач по математике для втузов, часть 3 « Теория вероятностей и математическая статистика» под ред. Ефимова А.В. М., « Наука», 1990 (имеется в библиотеке университета).

2. Вентцель Е.С. Теория вероятностей. – М: Высшая школа, 1999

3. Хрущева И.В. Основы математической статистики и теории случайных процессов [электронный ресурс]: учеб. пособие.- СПб.: Лань, 2009