46

Контрольная точка 1

1. Элементы математической статистики (2 лабораторных работы)

2. Z – преобразования и решение разностных уравнений

3. Характеристики динамических звеньев

Контрольная точка 2

4.Случайные процессы. Корреляционная теория.

5.Качественная теория решений ДУ. Фазовые портреты

6.Матричный способ решения систем линейных однородных дифференциальных уравнений порядка

Контрольная точка 3

7.Матричный способ решения систем линейных неоднородных дифференциальных уравнений порядка

8.Анализ систем линейных ДУ порядка

9.Элементы теории устойчивости

Контрольная точка 4

10.Элементы вариационного исчисления

РГР 1. Элементы математической статистики

Литература:

1. Сборник задач по математике для втузов, часть 3 « Теория вероятностей и математическая статистика» под ред. Ефимова А.В. М., « Наука», 1990 (имеется в библиотеке университета). Все ссылки даны на страницы этого задачника.

2. Казунина г.А. , Пинчина л.В. Элементы математической статистики с применением Excel [электронный ресурс]: учеб. Пособие, КузГту.- 2009

3. Д.М. Левин, д. Стефан, т.С. Кребиль, м.Л. Беренсон. Статистика для менеджеров с использованием Microsoft Excel/ Москва, Санкт-Петербург, Киев, “Вильямс”, 2005, 1310 с.

Лабораторная работа № 1

« Статистическое описание результатов наблюдений. Числовые оценки выборочного распределения. Интервальные оценки для математического ожидания и дисперсии. Проверка гипотезы о виде распределения»

1. Получите выборку из чисел

2. Постройте вариационный ряд (упорядочите элементы выборки по величине). При этом можно использовать соответствующую команду на панели инструментов Excel.

3 .Представьте выборку в виде группированного статистического ряда (с.178- 181)

• определите размах выборки

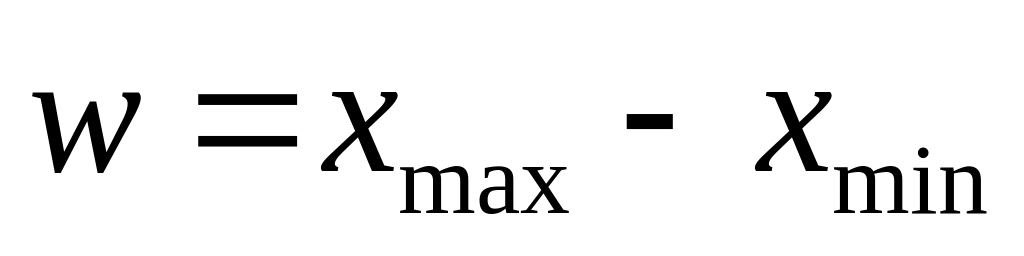
• определите число интервалов группировки одним из способов:

• а) Способ 1: выбираете число интервалов 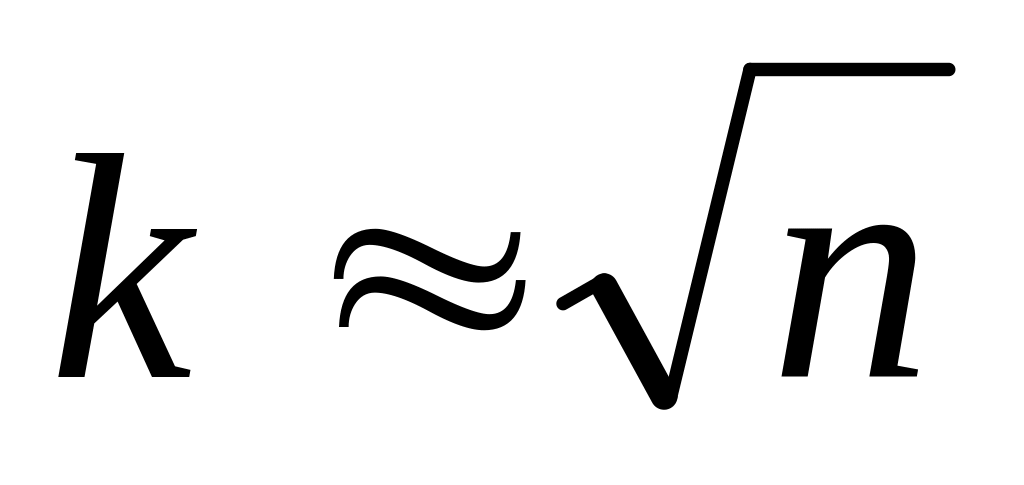, а затем находите шаг (ширину интервала группировки) 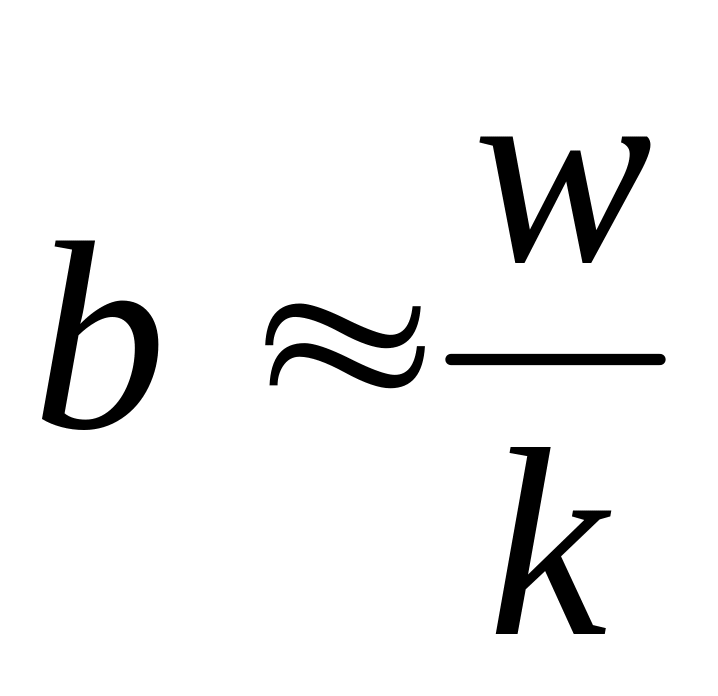, б) Способ 2: выбираете шаг (ширину интервала группировки) по формуле .

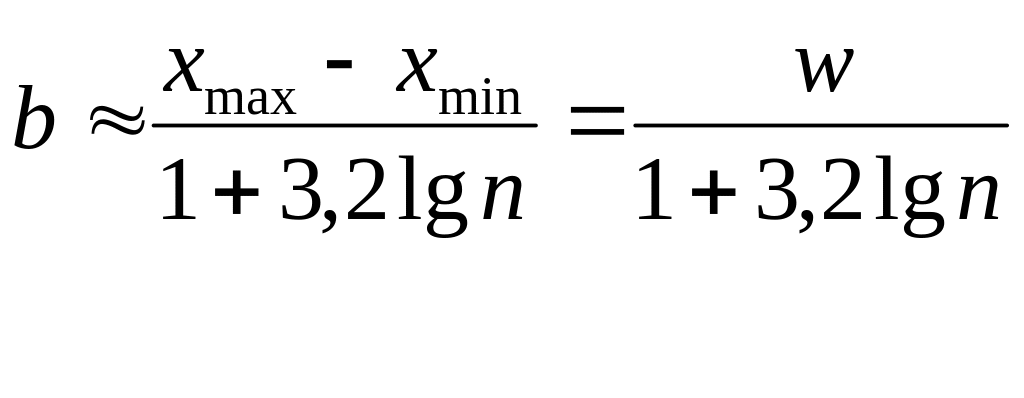• Определите границы интервалов группировки , и так далее до тех пор, пока наибольший элемент выборки не попадет в последний интервал ( наилучшая ситуация, если он точно совпадает с верхней границей последнего интервала)

• Найдите середину каждого интервала

• Определите частоты 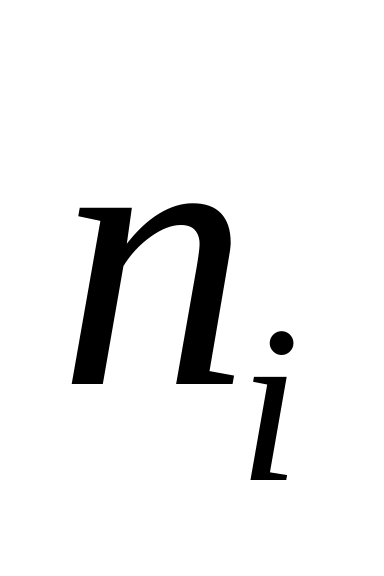- число элементов выборки, содержащихся в каждом 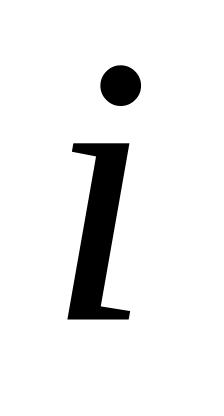-м интервале. При этом элемент, совпадающий с верхней границей интервала, условимся относить к следующему интервалу.

• Найдите накопленные частоты 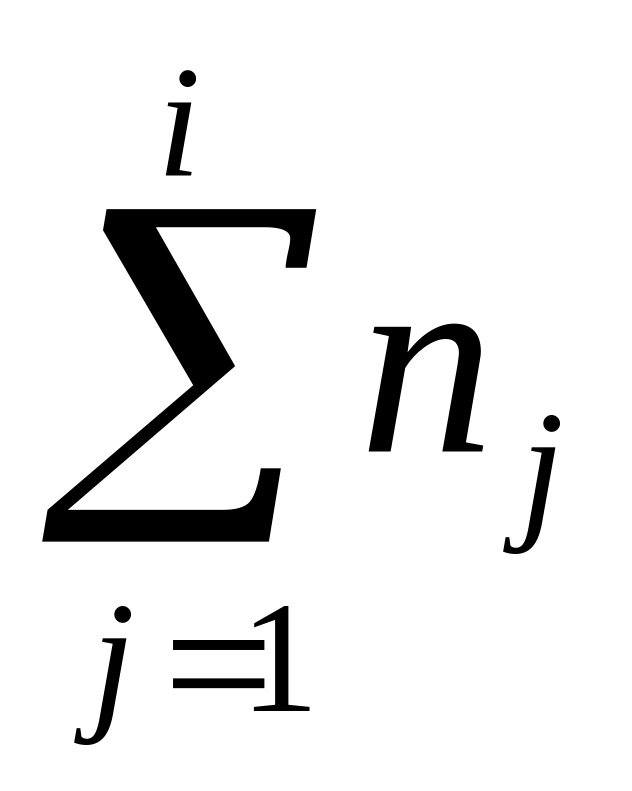. При этом сумма частот по всем интервалам должна совпадать с объемом выборки 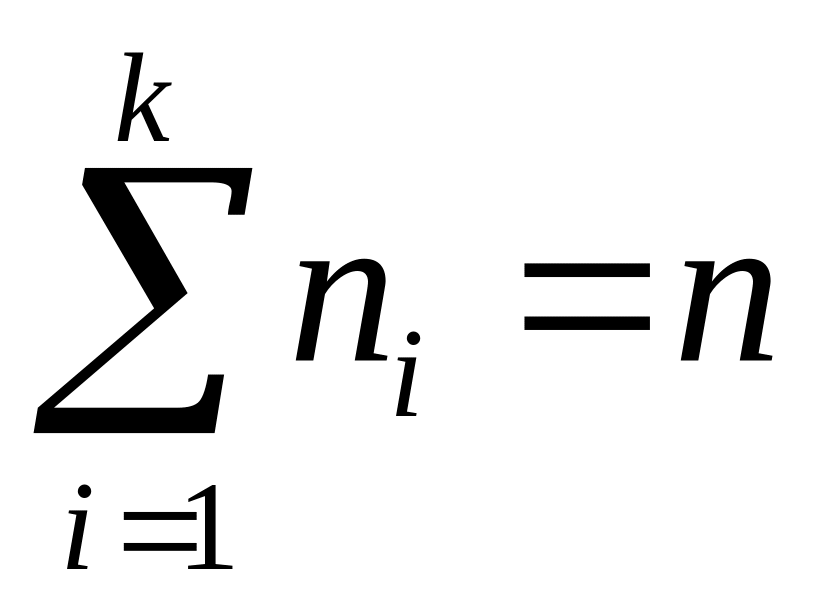. Если сумма частот по всем интервалам не совпадает с объем выборки, то следует проверить, правильно ли найдены частоты.

• Найдите относительные частоты , которые служат оценкой вероятности попадания элемента выборки в данный интервал

• Найдите относительные накопленные частоты 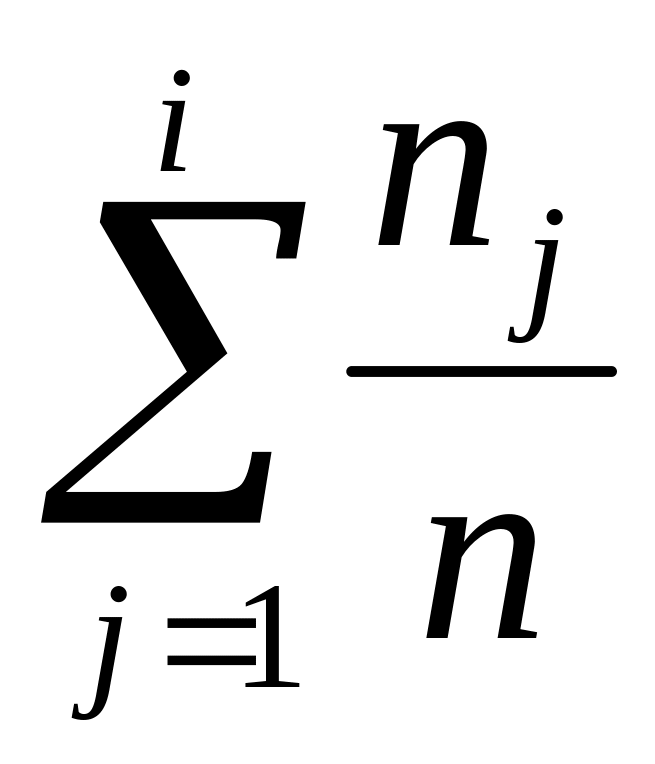. Значения накопленных частот служат оценкой функции распределения и определяют эмпирическую ( выборочную) функцию распределения

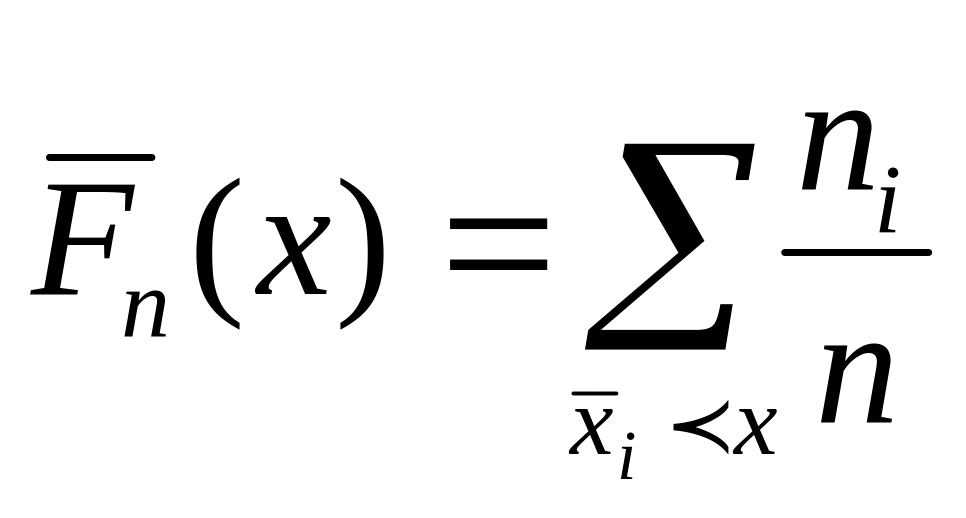
• Все полученные характеристики заносим в таблицу, которую называют статистическим рядом ( табл. 1.1 на стр. 181)

Номер интервала	Границы интервала	Середина Интервала	Частота	Накопленная Частота	Относитель- ная частота	Накопленная Относитель- ная частота

• Представить выборку графически (стр. 182-183)

• строим полигон частот- ломаную с вершинами в точках ( )

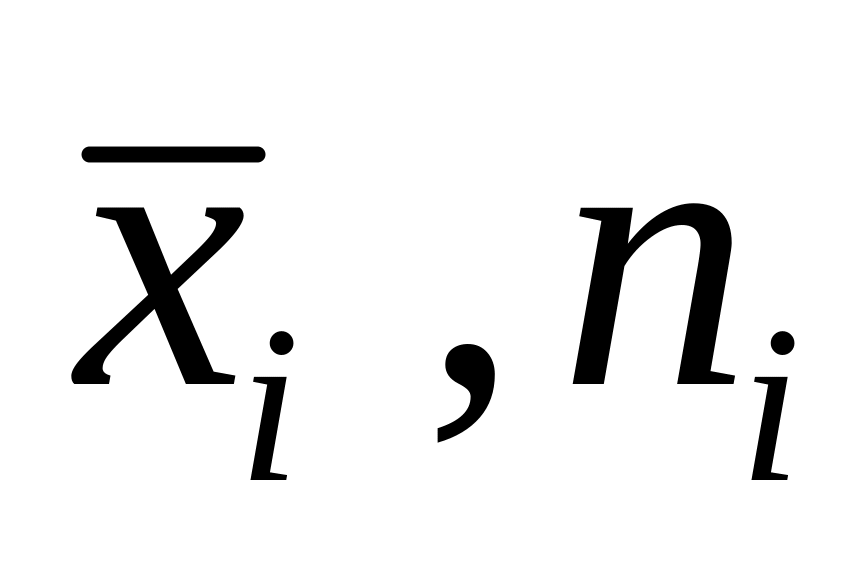• строим полигон относительных частот- ломаную с вершинами в точках ( )

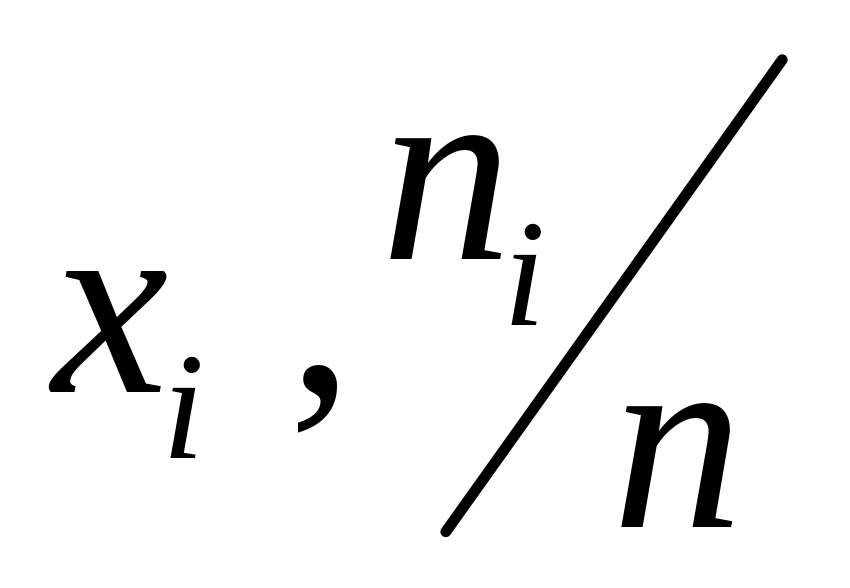• строим гистограмму - кусочно-постоянную функцию, которая на каждом интервале группировки принимает значение 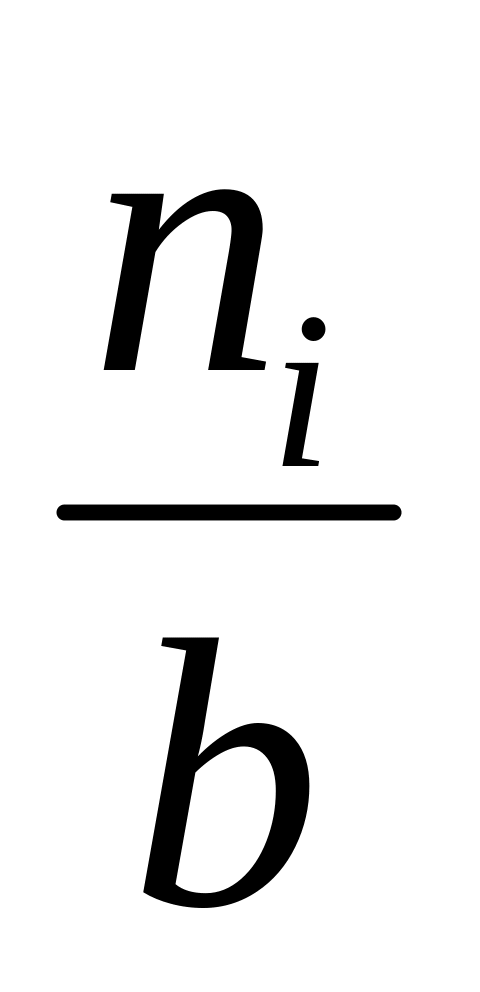. Площадь ступенчатой фигуры под графиком гистограммы равна объему выборки .

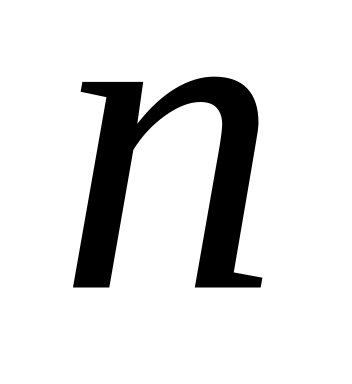Полигон относительных частот является статистическим аналогом функции плотности вероятности. Гистограмма и полигон частот отличаются от указанной характеристики растяжением в раз. Поэтому все данные функции также являются характеристиками закона распределения генеральной совокупности .

Примечание. Все перечисленные выше операции можно провести вручную или с использованием компьютерных программ. Самое доступное математическое обеспечение – Microsoft Excel при помощи команд: . При этом карманы (интервалы группировки) надо задать отдельно.

Пример выдачи данных.

4,050013		Размах		Шаг		Интервалы группировки
6,389652		9,538387		0,9538
6,633733						5,0038
6,763927						5,9576
6,919323						6,9114
7,095465						7,8652
7,329342						8,819
7,452228						9,7728
7,634686		Карман	Частота	Интегральный %		10,7266
7,647574		5,0038	1	1,00%		11,6804
7,69012		5,9576	0	1,00%		12,6342
7,83211		6,9114	3	4,00%		13,58
7,884502		7,8652	8	12,00%
8,052372		8,819	15	27,00%
8,083358		9,7728	23	50,00%
8,096873		10,7266	14	64,00%
8,128401		11,6804	19	83,00%
8,142575		12,6342	11	94,00%
8,36074		13,58	5	99,00%
8,398764		Еще	1	100,00%
8,418712
8,452986
8,495559

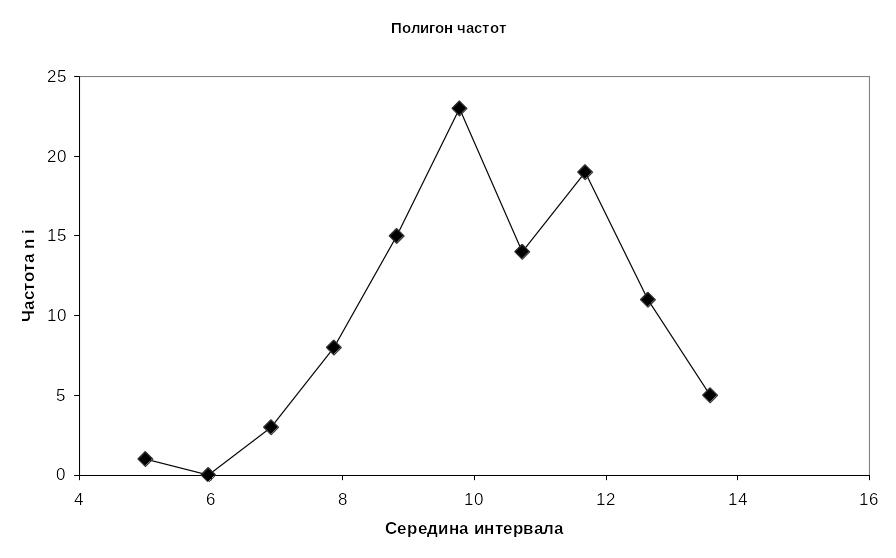
5. Определяем основные числовые характеристики выборочного распределения

• Оценкой математическоо ожидания является выборочное среднее

,

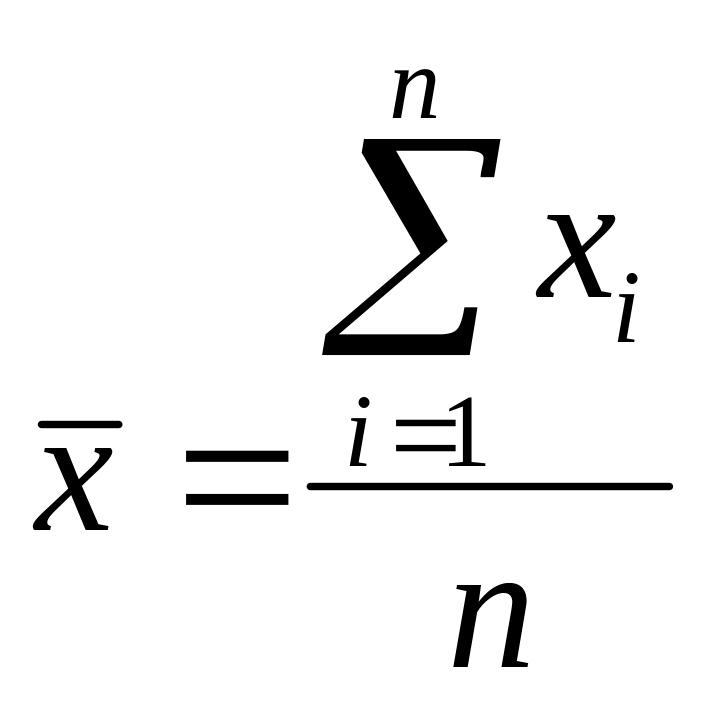если каждый элемент выборки встречается один раз.

• Если элемент выборки 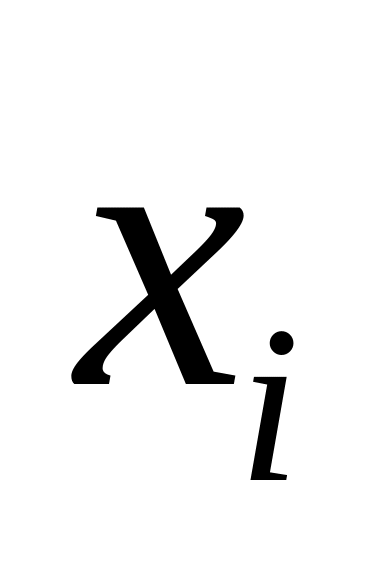имеет частоту , то выборочное среднеенаходят по формуле

.

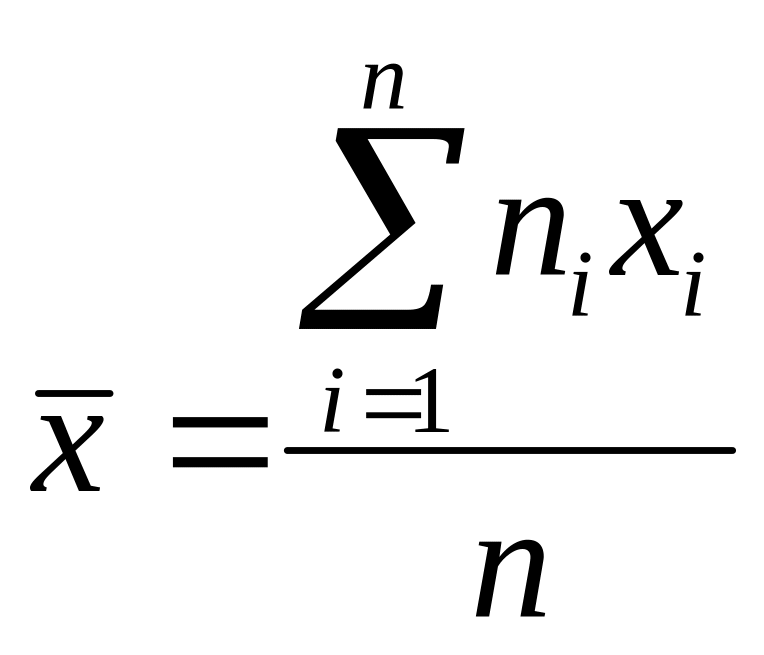В том случае, если выборка группированная, то вместо элемента выборки в этой формуле берут середину интервала, а за частоту берут число элементов, попадающих в данный интервал.

• Выборочная дисперсия служит оценкой дисперсии распределения генеральной совокупности и определяется по следующим формулам

Если каждый элемент выборки встречается только один раз и объем выборки достаточно велик ( ), то следует использовать формулу

• .

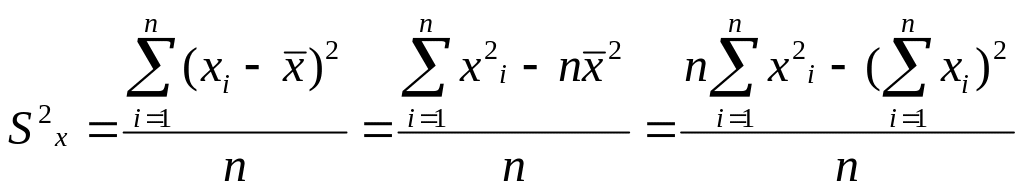Для выборок малого объема несмещенную (исправлннную) дисперсию следует вычислять по формуле

• 

Если частота каждого элемента , то для выборок большого объема следует использовать формулу

.

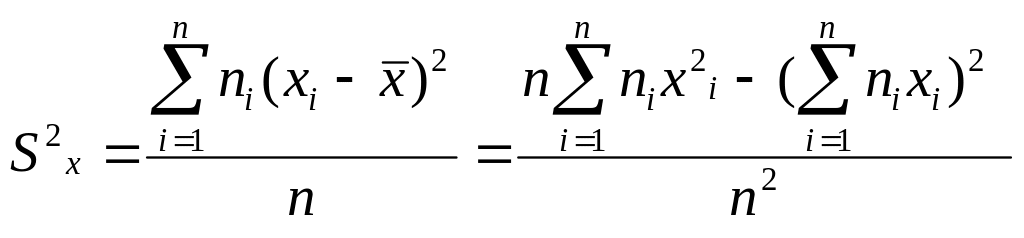Для группированных выборок в этой формуле нужно использовать середину интервала и число элементов, попадающих в этот интервал.

Для вычислений вручную подробнее см. стр. 189-191

Все перечисленные операции можно выполнить в Excel согласно командам

Пример выдачи данных:

Столбец1
Среднее	9,899346449
Стандартная ошибка	0,177148981
Медиана	9,79959739
Мода	11,52953362
Стандартное отклонение	1,771489807
Дисперсия выборки	3,138176135
Эксцесс	0,060472776
Асимметричность	-0,273471727
Интервал	9,531831893
Минимум	4,050012901
Максимум	13,58184479
Сумма	989,9346449
Счет	100
Уровень надежности(95,0%)	0,351502073