Теоретическая часть

Наиболее естественным аппаратом приближения периодических функций f(x) являются частные суммы их ряда Фурье. Однако последовательности не являются равномерно сходящимися на всем классе непрерывных функций. Тем не менее, исходя из частных сумм Фурье, можно построить последовательности полиномов (полиномы Фейера, Джексона, Валле - Пуссена, Бернштейна - Рогозинского и др.), которые равномерно сходятся для любой непрерывной периодической функции.

Одним из наиболее общих способов построения таких полиномов является суммирование рядов Фурье, сущность которого заключается в том, что с помощью заданных двух треугольных матриц чисел и , где n=0,1,2,... и k=0,1,...,n, каждой 2p - периодической функции f(x) ставится в соответствие полином вида

(4.1)

где и - коэффициенты Фурье функции f(x). Таким образом, каждой парой матриц L и M определяется конкретный линейный метод U(L,M) суммирования рядов Фурье.

Будем считать, что и .

Рассмотрим некоторые конкретные примеры линейных методов суммирования.

А) Метод частных сумм ряда Фурье. Он получается при . В этом случае

(4.2)

Б) Метод средних арифметических (метод Фейера) получается при Тогда

(4.3)

В) Метод Валле - Пуссена получим, полагая

В этом случае

(4.4)

Г) В случае, когда получаем метод Рогозинского . Тогда

(4.5)

Указания к выполнению лабораторной работы

1. Отладить программу для функции, не имеющей никаких особых точек.

2. Приблизить функцию с помощью всех выше указанных методов. Результаты приближения сравнить.

3. Погрешность приближения оценить в метрике пространства .

Контрольные вопросы

1. Для чего нужны методы суммирования рядов Фурье?

2. Каковы достаточные условия существования ряда Фурье для функции f(x)?

Варианты заданий

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

20. 

21. 

22. 

23. ;

24. 

25. 

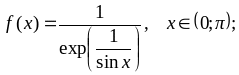
Лабораторная работа № 5

Разложение функций в ряд по ортогональным многочленам

Цель работы: исследование приближения функций посредством их разложения в ряды по ортогональным многочленам.

Постановка задачи. Приблизить функцию f(x), разложив ее в ряд Фурье - Чебышева первого и второго рода, а также в ряд Фурье - Лежандра. Исследовать точность и устойчивость разложений, оценить влияние особых точек функции на устойчивость и точность.

Теоретическая часть

Рассмотрим многочлены Чебышева первого рода

(5.1)

Для многочленов (5.1) справедливо рекуррентное соотношение

(5.2)

Многочлены Чебышева (5.1) ортогональны на сегменте [-1,1] с весовой функцией . Справедливо соотношение

(5.3)

Следовательно, ортонормированные многочлены Чебышева первого рода выражаются через многочлены (5.1) следующим образом:

(5.4)

Если функция f(x) задана на сегменте [-1,1] и интегрируема с весом , то, определяя коэффициенты Фурье - Чебышева

(5.5)

этой функции, поставим в соответствие ряд Фурье по многочленам Чебышева первого рода

(5.6)

Многочлены Чебышева второго рода определяются формулой

(5.7)

Рекуррентное соотношение для многочленов Чебышева второго рода имеет вид

(5.8)

Многочлены (5.6) ортогональны на сегменте [-1,1] с весом Справедливо соотношение

Следовательно, ортонормированные многочлены Чебышева второго рода выразятся по формуле

(5.9)

Пусть на сегменте [-1,1] задана функция f(x), интегрируемая с весом Тогда, определяя коэффициенты Фурье по формуле

, (5.10)

поставим в соответствие функции f(x) ее ряд Фурье по многочленам Чебышева второго рода

(5.11)

Многочлены Лежандра определяются формулой Родрига

(5.12)

Многочлены Лежандра ортогональны на сегменте [-1,1] с весом h(x)=1. Справедливо соотношение

Следовательно, ортонормированные многочлены Лежандра имеют следующий вид

(5.13)

Если функция f(x) интегрируема на сегменте [-1,1], то можно определить коэффициенты Фурье по многочленам Лежандра

(5.14)

и поставить этой функции в соответствие ряд Фурье - Лежандра

(5.15)

Указания к выполнению лабораторной работы

1. Исследовать точность приближения заданной функции с помощью разложения в ряды по ортонормированным многочленам, рассматривая n-тые частные суммы разложений вида (5.6), (5.11) и (5.15).

2. Значения многочленов Лежандра вычислять по рекуррентной формуле (1.7).

3. Погрешность оценить в метрике .

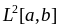Контрольные вопросы

1. При выполнении каких условий, налагаемых на приближаемую функцию f(x), ряды Фурье - Чебышева и Фурье - Лежандра будут сходиться к f(x)?

2. Что такое ортогональная и ортонормированная система функций?

3. Обоснуйте справедливость формул (5.5), (5.10) и (5.14), определяющих коэффициенты разложения функции в ряд по ортонормированным многочленам.

Варианты заданий

1. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

20. 

21. 

22. 

23. 

24. 

25. 

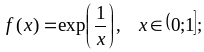
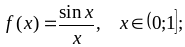
    Лабораторная работа № 6

    Приближение функций локальными сплайнами

Цель работы: исследование приближения функций одной переменной с помощью локальных сплайнов.

Постановка задачи. Аппроксимировать функцию f(x) локальными сплайнами. Исследовать точность и устойчивость приближения. Оценить влияние особых точек функции на точность и устойчивость.

Теоретическая часть

Сплайнами называют функции, «склеенные» из «кусков» многочленов. Функция s(t), заданная и непрерывная на отрезке [a,b], называется сплайном порядка m с узлами если на каждом из промежутков представляет собой алгебраический многочлен степени, не превосходящей m, т.е.

для (6.1)

а в каждой из точек некоторые производные могут иметь разрыв.

Сплайн s(t) порядка m имеет дефект в узле , если в точке непрерывны функции а производная в точке терпит разрыв. Число называется дефектом сплайна s(t).

В качестве простейшего сплайна порядка m можно рассмотреть функцию, построенную следующим образом.

На сегменте [-1,1] рассмотрим узлы многочлена Чебышева . Отобразим их на каждый из сегментов , причем таким образом, что узел переходит в точку , а узел - в точку . По полученным узлам на каждом сегменте построим многочлен Лагранжа порядка m. За счет выше указанного выбора узлов мы как бы склеиваем полиномы. В результате получим непрерывную функцию - сплайн.