Лекция 22
3.27. Размещение полюсов замкнутой цифровой системы с помощью обратной связи по состоянию
Аналогично задаче рамещения полюсов непрерывной системы проблема размещения полюсов замкнутой системы ставится следующим образом.
Дано: уравнения ОУ в переменных состояния
(1)
,
(2)
где
n-
вектор состояния полностью измерим.
Закон управления с обратной связью по
состоянию имеет вид
,
где
-
коэффициент обратной связи по состоянию.
При этом уравнение замкнутой цифровой
системы
содержит системную матрицу
,
собственные значения zi которой, другими словами, полюсы замкнутой сситемы зависят от выбора коэффициента .
Требуется найти коэффициент обратной связи по состоянию так, чтобы эти полюсы были равны полюсам желаемой системы zi*. Эта задача может быть решена в рамках MATLAB с помощью процедуры acker.
3.28. Цифровой (дискретный) лкр-регулятор
Кроме того, возможно определение коэффициентов для цифрового ЛКР-регулятора, исходя из квадратичного критерия качества
,
(2а)
где Q и R симметричные неотрицательно определенные весовые матрицы.
Матрица Q определяет стоимость штрафа, назначаемого за отклонение переменных состояния относительно их знчений в состоянии равновесия. Матрица R определяет стоимость штрафа, наначаемого за величину (уровень) управляющего воздействия. Эти матрицы устанавливаются пректировщиком системы. Цель управления принудить переменные состояния быть как можно ближе к нулю, в то время как штрафуется управляющее воздействие.
Итак,
задача цифрового ЛКР управления
заключается в том, чтобы найти такое
управление u[i]
(см. рис. ниже), которое минимизирует
критерий качества
при условии, что объект управления
описыватся уравнением
и
задано начальное состояние
.
Оптимальное решение представляет собой обатную связь по состоянию
,
где векторный коэффициент обратной связи по состоянию имеет вид
.
В последнем выражении матрица P является решением линейного алгебраического разностного уравнения
.
При
этом замкнутая система независимо от
выбора весовых матриц является устойчивой,
т.е. все собственные значения матрицы
замкнутой системы
имеют модули, меньшие единицы и значение
оптиального критерия качества равно
.
Итак,
минимизирует
.
Пример.
При
объектах высокого порядка для определения
P
и
целесообразно применить команду dlqr
системы MATLAB.
3.29. Цифровой наблюдатель состояния
Если не измерим, то для реализации обратной связи по состоянию как в задаче размещения полюсов, так и в задаче ЛКГ управления, выбирают другой закон управления
,
в
котором оценка состояния
определяется с
помощью цифрового наблюдателя состояния,
описываемого уравнением
.
(3)
Здесь
.
При этом ошибка
оценки
может быть представлена уравнением
,
(*)
в
котором матрица наблюдателя равна
.
Коэффициент
выбирается исходя
из желаемого расположения полюсов
наблюдателя, т.е. корней характеристического
уравнения
.
Можно
выбрать
так, чтобы все
полюсы наблюдателя располагались в
начале координат комплексной плоскости
.
При этом
и переходный
процесс в наблюдателе заканчивается
за конечное число периодов дискретизации.
Такой наблюдатель получил название
апериодического
наблюдателя.
При использовании закона управления с
обратной связью по оценке состояния
цифровая система имеет полюсы, являющиеся
объединением полюсов, котрые соответствуют
выбранному значению коэффициента
,
и полюсов наблюдателя, соответствующих
выбранному значению
.
Эта теорема
разделения,
разумеется, справедлива как для задачи
размещения полюсов, положение которых
выбирается проектировщиком системы,
так и для цифровой задачи ЛКГ управления,
когда расположение полюсов находится
путем решения оптимизационной задачи.
3.30. Оптимальный цифровой наблюдатель состояния (Фильтр Калмана)
Пусть
на ОУ первого порядка (n
= 1) влияет
случайное возмущающее воздействие f[i]
(так называемый шум
объекта) в
виде белого шума c
нулевым математическим ожиданием и
дисперсией
,
так что скалярное уравнение состояния
имеет вид
.
(4)
Управляемая
величина
=x[i]
в результате прохождения через датчик
искажается случайным
шумом датчика
s[i]
в виде белого шума c
нулевым математическим ожиданием и
дисперсией
.
В результате на выходе датчика образуется
наблюдаемая последовательность
,
(5)
называемая
в дальнейшем измеренной величиной.
Также предположим, что математическое
ожидание начального состояния объекта
равно нулю, т.е.
.
В 1949 г. американский ученый Винер разработал процедуру решения задачи фильтрации применительно к непрерывным стационарным системам.
Около полувека назад американский ученый Калман предложил искусную стратегию, позволяющую уменьшить дисперсию ошибки оценивания вектора состояния, обусловленную шумами объекта и датчика. Эта стратегия является вариантом (версией) наблюдателя состояния, рассмотренного в предыдущем параграфе. Там для определения оценки состояния на один период дискретизации вперед
используется
полученное по прошлым измерениям с
помощью уравнения ОУ предсказанное
значение состояния
,
которое корректирутся слагаемым,
пропорциональным разности между
фактически измеренной управляемой
величиной
и ее предсказанным значением
.
Здесь стратегия аналогичная, однако,
вследствие того, что как предсказанное
значение состояния, так и фактически
измеренная управляемая величина
подвержены искажению шумами (возмущение
и шум измерения), желательно найти такую
их комбинацию, которая минимизирует
общую неопределенность относительно
оценки состояния. Хотя, подобно
наблюдателю, основная идея - дополнить
предсказанное значение фактически
измеренными данными, чтобы получить
более полную оценку вектора состояния.
Мы в начале введем обозначения для одной величины, которая описывает состояние объекта в момент i+1:
предсказанное значение состояния
,
и для другой величины, которая описывает измерение в момент i+1:
предсказанное значение измеряемой величины
,
определяемое
по всем предыдущим измерениям вплоть
до
:
.
При этом
из (4) и
из (5) будем называть истинным
состоянием
и фактическим
измерением
соответственно. Кроме
того, введем в рассмотрение « лучшую
оценку состояния»
,
которая является линейной комбинацией предсказанного значения и измеренного значения состояния.
Обладание
этими уравнениями половина дела. В
последнем уравнении «коэффициент
усиления Калмана»
должен быть выбран
так, чтобы минимизировать общую
неопределенность в
путем линейной
комбинации с соответствующими весами
двух частей информации, которая нам
доступна: 1) лучшей оценке
,
основанной на предудущих измерениях и
динамических свойствах объекта
управления, и 2) фактическом измерении
.
Обозначение
означает, что
оценка
получена с использованием всех предыдущих
измерений вплоть до
.
Заметим, что
истинное состояние x
заранее неизвестно.
Наша
цель найти оптимальное значение для
коэффициента усиления Калмана
.
Чтобы добиться
этого, запишем оценку
=
как
(6)
в стандартной присущей наблюдателю форме (3), используя (4) и (5). Определяя ошибку оценки , легко показать, используя (1), (2) и (6), что
.
(7)
Как
видим, в отсутствие шумовых слагаемых
и
уравнение
существенно упрощается до полученного
ранее уравнения для ошибки оценки (*)
.
В данном случае
есть скалярная величина.
При этом ключевым моментом является «лучший» метод выбора коэффициента усиления Калмана. Т.к. все сигналы, входящие в выражение для ошибки (7) являются случайными, то и сама ошибка есть случайная последовательность. Поэтому в качестве критерия точности оценивания выбираем дисперсию ошибки оценки в момент i+1
.
(8)
Математическое ожидание ошибки в соответствии с уравнением (7)
.
Здесь
мы учли, что математические ожидания
шумов объекта и датчика равны нулю.
Т.к. математическое ожидание начального
состояния объекта равно нулю, то, выбирая
также равным нулю начальное состояние
фильтра Калмана
,
получаем нулевое значение математического
ожидания ошибки оценивания для всех
значений i
> 0,
=
-
=0.
Тогда из (7) и (8) имеем
.
(9)
В (9) математические ожидания перекрестных величин равны нулю, т.к. по предположению шумы датчика и объекта, и ошибка оценки некоррелированы между собой:
.
Дифференцируя (9) по и приравнивая результат нулю, мы получаем уравнение
.
Отсюда минимум дисперсии будет иметь место, если выбран как
.
(10)
При этом минимальная дисперсия ошибки оценки
,
(11)
причем
.
Мы ввели аргумент
i+1
для
,
т.к. в общем случае минимизация должна
осуществляться в каждый дискретный
момент времени, и динамические свойства
объекта (в данном случае параметр a)
и статистические свойства шумов могут
явно зависеть от времени.
Из
(10) вытекает, что, если значение
большое (большой
шум объекта) и значение
малое (малый шум датчика), то
1. В этом
случае
согласно
надо доверять результатам измерений,
т.е.
.
Альтернативно, если шум датчика
доминирует, нужно отдать предпочтение
предсказанному значению
,
взяв
0. Уравнение (10)
дает оптимальный баланс между этими
крайними значениями. Файл kalman.m
в Matlab6.5.
Обсуждение проблем построения фильтра Калмана касалось лишь объекта первого порядка. Однако для объекта n-го порядка результаты получаются подобным образом с точными векторно-матричными аналогиями уравнений, рассмотренных выше. Алгебраические выражения выглядят более сложными, но все основные рассуждения остаются теми же самыми. Моделям (4) и (5) соответствуют выражения
(11а)
(11b)
и
структурная схема, представленная на
рис. ниже. Здесь
оператор сдвига в сторону запаздывания
на один период дискретизации,
и
̶ дискретные гауссовские белые шумы
(белые случайные последовательности)
со с нулевыми математическими ожиданиями
и ковариационными матрицами:
Кроме
того, предполагается, что начальное
состояние x[0]
имеет нормальное распределение с
математическим ожиданием
и ковариацией
Обобщение уравнений (6) и (9) приводит к векторно-матричным уравнениям
(12)
(13)
Здесь
матрица
дисперсий векторной ошибки оценки в
момент i+1,
матрица дисперсий векторного шума
объекта,
матрица дисперсий векторного шума
датчика. Минимума дисперсии
добиваемся,
выбирая матричный
коэффициент фильтра Калмана в виде
.
При этом сам минимум дисперсии ошибки определяется выражением
,
где
и
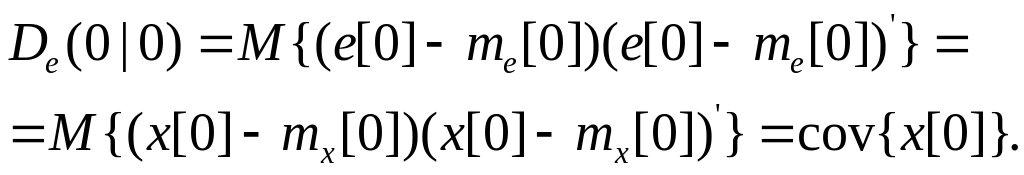
Замечание.
Фильтр Калмана в (12) обладает тем
свойством, что состояние в момент i
определяется
по известным значениям
Можно построить фильтр, в котором для
оценивания
используются
Соответствующие
уравнения имеют вид
(14)
где
,
(15)
На рис. ниже показана структурная схема фильтра Калмана, построенная с использованием уравнений (14).
Пример. Рассмотрим объект первого порядка
,
.
Пусть
дисперсия шума измерения
=1,
и среднее значение
=2
и диперсия
.
Состояние
постоянно и
должно быть определено из зашумленных
данных. Фильтр Калмана в соответствии
(14) и (15) описывается следующими уравнениями:
(16)
,
(17)
Дисперсия и коэффициент усиления Калмана убывают со временем. На рисунках ниже показано как изменяется ошибка оценки при использовании фильтра Калмана и уравнения (16) при постоянном значении . При большом постоянном значении =0.08 ошибка быстро убывает, однако в установившемся состоянии дисперсия довольно велика, При небольшом постоянном значении =0.01 ошибка убывает медленно, но в установившемся состоянии дисперсия меньше. Файл kalman.mdl в MATLAB 6.5.
Итак, минимизирует
