
Лекция 2
.pdfПроф. Власов А.Н. Материалы лекций по курсу «ОБЩАЯ ФИЗИКА» 2015
1-й семестр.
Лекция № 2
Тема лекции:
Кинематика
План:
1.Кинематика и механическое движение….……………….…………………..…1
2.Число степеней свободы системы…………...………………………………….4
3.Скорость материальной точки…………………………………………….…….8
4.Ускорение материальной точки ……………….……………………..……...…12
5.Тангенциальное и нормальное ускорение..….……………………………...…14
6.Вращательное движение…………………………… ..…………………..….....16
7.Кинематика твѐрдого тела………………………………………………………21
1.Кинематика и механическое движение
Вкинематике изучаются пространственно-времен- ные характеристики механического движения. При этом причины движения, т. е. взаимодействия между телами, не рассматриваются.
Механическое движение – это перемещение объекта в пространстве со временем. Это движение имеет строго определенное содержание только при указании, относительно каких тел перемещается рассматриваемый объект. Поэтому для описания механического движения необходимо ввести систему отсчета.
1
Система отсчета включает тело отсчета для фиксации положения рассматриваемого объекта и эталонный процесс для фиксации времени.
Эталонный процесс фиксации времени реализуется в часах. С помощью часов отмечаются моменты времени, соответствующие мгновенным положениям движущегося тела.
Совокупность тела отсчета, системы координат и часов называется системой отсчета.
Пространство и время не существуют отдельно от материи.
Пространство выражает порядок сосуществования материальных объектов, время отражает порядок смены явлений.
Не существует явлений, которые протекали бы вне пространства и времени. Пространство и время, как формы существования материи, органически связаны между собой: наблюдаемый мир четырехмерен.
Три измерения — пространственные, одно измерение
связано со временем.
Примером простейшей системы координат служит
прямоугольная декартова система координат. Она реа-
лизуется тремя взаимно перпендикулярными плоскостями, жестко связанными с телом отсчета. Точка их пересечения называется началом координат, а линии их пересечения — координатными осями.
2
Координатами точки служат три расстояния от нее до координатных плоскостей, обычно обозначаемые x , y ,
z 0
.
x
Соответствующие координатные оси обозначаются
, 0 y , 0 z .
Чаще всего используется «правовинтовая» система декартовых координат. Если в такой системе посмотреть с
конца орта |
|
||
e |
|||
|
|
|
z |
оси |
x |
к |
оси |
на оси |
x |
и |
y |
будет |
y , то кратчайший поворот от происходить против часовой
стрелки. Это соответствует связям между ортами коор-
динатной системы: |
|
|
|
|
|
|
, |
|
|
|
|
|
|||
e |
z |
e |
x |
,e |
y |
||
|
|
|
, |
||||
|
|
|
|
|
|
||
e |
x |
e |
y |
,e |
z |
||
|
|
|
|
||||
|
|
|
|
. |
|||
e |
y |
e |
z |
,e |
x |
||
|
|
|
|
|
|||
В кинематике число принципиально равноценных систем координат бесконечно.
Стремятся использовать такую систему, которая максимально облегчает решение рассматриваемой задачи.
Кроме декартовой системы координат используются цилиндрическая и сферическая системы (см. Лекцию № 1).
Число независимых координат, однозначно определяющих положение тела (или системы тел) в пространстве, называется числом степеней свободы тела (или системы тел).
3

2. Число степеней свободы системы
В общем случае число степеней свободы системы не совпадает с общим числом пространственных координат. Более того, величины, о которых идет речь в определении числа степеней свободы, не обязательно должны иметь смысл пространственных координат, поскольку в зависимости от условий задачи может оказаться более удобным выбор каких-либо других координат.
Любые
k
величин
q |
, q |
, ...,q |
1 |
2 |
k |
,
однозначно
определяющие положение системы, называют ее
обобщенными координатами. К примеру, это могут быть скорости точек.
У одной свободной материальной точки число обоб-
щенных (как и декартовых) координат равно трем, т. е. число степеней свободы в этом случае k 3; у N -точек
k 3N . |
|
|
|
Если точка не свободна, а движется, например, по |
|||
поверхности сферы |
заданного радиуса |
R с центром в |
|
начале координат, |
то три координаты |
x, y, z |
связаны |
между собой соотношением R 
 x2 y2 z2 .
x2 y2 z2 .
Иными словами, имеются только две независимые координаты. Задавая их, можно из приведенного выражения найти третью. В этом случае говорят, что на систему «материальная точка» наложена одна жесткая
связь.
4

Следовательно, при наличии одной жесткой связи
число степеней свободы убывает на единицу и
становится равным |
k 3 - n 3 - 1 2 , |
где n — число |
связей, т. е. достаточно ввести две координаты, например, |
||
x, y , и положение |
точки будет задано |
однозначно. В |
таком случае |
обобщенными координатами будут |
q1 x, q2 y . |
|
Если точка может двигаться вдоль заданной кривой, то число степеней свободы уменьшается до одной, так как
число |
связей |
увеличивается |
до |
n 2; |
k 3 - n 3 - 2 1. |
Например, точка |
может |
перемещаться по сфере с радиусом
плоскости xOy , т. |
е. по окружности |
лежащей в плоскости |
xOy . |
В этом случае на координаты точки
R с
x,
, оставаясь |
в |
радиусом |
R , |
y, z наложены |
|
две связи: |
R |
x |
2 |
y |
2 |
z |
2 |
— уравнение сферы и |
|
|
|
z 0 — уравнение плоскости. В качестве обобщенной координаты можно выбрать q x .
Можно также перейти к сферическим координатам и выбрать q .
В общем случае число степеней свободы тела или системы тел и, следовательно, число обобщенных координат
k 3N - n ,
5

где
тела
N — число материальных точек, входящих в состав или системы тел, n — число связей.
A
У
x |
, |
1 |
|
|
«жесткого» |
треугольника |
|
|||||||
y ,z |
, |
B x |
, y ,z |
2 |
, |
C x |
, y ,z |
|
||
1 |
1 |
|
2 |
2 |
|
3 |
3 |
3 |
|
|
с вершинами число степеней
свободы |
k 3N - n 6 |
, |
где |
||||||
наложенных |
|
|
|
|
|
на |
|||
x |
, y |
, z |
, x |
, y |
, z |
, x |
, y |
, z . |
|
1 |
1 |
1 |
2 |
2 |
2 |
3 |
|
3 |
3 |
следующий вид:
n 3 |
— |
число |
связей, |
|
|
координаты |
|
Уравнения |
связей |
имеют |
|
l |
|
x |
x |
2 |
y |
|
y |
|
|
|
2 |
z |
|
z |
|
|
2 |
|
const , |
|
2 |
|
|
|
2 |
|
|
|
|||||||||||
12 |
|
2 |
1 |
|
1 |
|
|
|
1 |
|
|
|
|
||||||
l |
|
x |
|
2 |
y |
|
y |
|
|
|
2 |
z |
|
z |
|
|
2 |
const , |
|
x |
|
|
|
|
|
||||||||||||||
13 |
|
3 |
1 |
|
3 |
1 |
|
|
|
3 |
1 |
|
|
|
|
|
|||
l |
|
x |
x |
2 |
y |
y |
|
|
|
2 |
z |
z |
|
|
2 |
const . |
|||
|
2 |
|
2 |
|
|
||||||||||||||
32 |
|
3 |
2 |
|
3 |
|
|
|
3 |
|
|
|
|
||||||
Здесь |
l |
,l |
,l |
|
12 |
13 |
32 |
треугольника.
- длины трѐх сторон рассматриваемого
«Жесткий» треугольник моделирует абсолютно твердое тело, поэтому и у произвольного свободного твердого тела число степеней свободы также будет равно 6, из которых 3 описывают поступательное, а 3 — вращательное движения тела.
Если твердое тело закреплено в точке (еще 3 дополнительных связей), то оно может лишь вращаться вокруг этой точки — остается только три степени свободы.
6
У твердого тела, могущего вращаться вокруг закрепленной оси, остается одна степень свободы, характеризуемая одной обобщенной координатой — углом поворота вокруг этой оси.
Итак, для описания механического движения тела или системы тел необходимо, прежде всего, задать систему
отсчета.
Описание механического движения тела означает описание механического движения всех отдельных малых частей этого тела.
Под малыми частями тела подразумеваются такие, которые можно считать материальными точками.
Таким образом, задача кинематического описания
движения тел или системы тел сводится к таковой для
материальной точки.
7
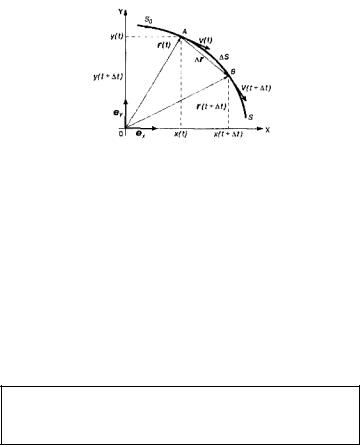
3. Скорость материальной точки
Для описания механического движения материальной точки введем систему отсчета, включающую декартову систему координат x, y, z и часы, отсчитывающие время
t (рис. 1).
Рис. 1 |
|
На рис. 1 изображена линия |
S , которую описывает |
движущаяся точка. Линия, которую описывает при своем движении точка, называется траекторией.
Введем в рассмотрение вектор, соединяющий начало
координат и положение точки в данный момент времени |
||
t . Обозначим его |
|
. Этот вектор называется радиус- |
r |
||
вектором. Очевидно, что при движении точки радиусвектор будет изменяться, т. е. он является функцией времени. Эта функция называется уравнением движения точки в векторной форме:
r r |
t x t , y t , z t xex yey zez . |
|||
|
|
|
|
|
8

Проекции |
вектора |
|
t |
r |
|||
представляют |
собой уравнения |
||
координатной форме: |
|
|
|
на оси координат
движения точки в
x x t , y y t , z z t .
Уравнения движения, как в векторной форме, так и в координатной форме содержат полную информацию о механическом движении точки.
Путь S |
— это длина отрезка траектории, проходи- |
|
мого точкой |
от некоторого начального положения |
S |
|
|
0 |
до положения ее в данный момент времени. |
|
|
Иногда применяется так называемый естественный способ описания движения. При этом задается уравнение траектории движения точки и зависимость пути от
времени S S t . Однако этот способ удобен только в
случае простых траекторий, например, прямой или окружности.
Важным понятием кинематики является вектор перемещения r (см. рис. 1). Этот вектор соединяет два
последовательных положения точки на траектории. В общем случае он равен разности радиус-векторов двух последовательных положений точки на траектории.
9

|
|
|
Путь |
S |
и перемещение |
траектория |
прямолинейна |
|
бесконечно малый отрезок пути.
r
или
совпадают, если рассматривается
Вектор перемещения используется для введения основных кинематических характеристик механического движения материальной точки — мгновенной скорости и ускорения. Эти характеристики используются также в динамике.
Рассмотрим еще раз рис. 1. Возьмем отношение вектора
перемещения точки из положения в положение
r A B
к промежутку времени t , разделяющему эти положения. Отношение
|
|
t |
|
|
|
|
r |
t t r |
|
r |
t, t t |
||
|
|
|
|
v |
||
|
t |
|
|
t |
ср |
|
|
|
|
|
|
представляет собой вектор средней скорости перемеще-
ния между точками |
A и B . |
|
|
|
|
|||
|
Мгновенная скорость |
|
материальной точки в |
|||||
|
v |
|||||||
положении A равна: |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
dr |
|
||
|
|
v lim |
|
|
r , |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
t 0 |
t |
|
dt |
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r — первая производная радиус-вектора по времени. |
||||||||
|
|
|
|
|
|
|
|
|
Из способа нахождения мгновенной скорости ясно, что она всегда направлена по касательной к траектории.
10
