Лекция №4 ММвХТ 8 ноября 12

Решение обыкновенных дифференциальных уравнений в smath studio (задача коши) Введение

Инженерные исследования динамики процессов, протекающих в механизмах, реакторах, локальных системах стабилизации параметров технологических процессов, трубопроводах, теплообменных процессах и других химических объектах приводят к дифференциальным уравнениям, т.е. уравнениям, содержащим производные. Например: уравнение колебания массы под воздействием силы, изменение концентрации растворов, уравнение накопления и стекания заряда на обкладках конденсатора.

Классические методы решения обыкновенных дифференциальных уравнений часто на практике либо приводят к сложным решениям, либо вообще неприменимы (коэффициенты или функции в дифференциальном уравнении содержат существенные нелинейности либо заданы в виде таблиц экспериментальных данных).

Поэтому большое значение приобретают методы приближенного интегрирования дифференциальных уравнений, которые в зависимости от формы представления решения можно разделить (условно) на три группы:

1) аналитические, дающие приближенное решение дифференциального уравнения в виде аналитического выражения;

2) графические, дающие приближенное решение в виде графика;

3) численные, дающие приближенное решение в виде таблицы.

Рассмотрим численные методы решения обыкновенных дифференциальных уравнений.

1. Постановка задачи численного метода решения дифференциальных уравнений

Дано обыкновенное дифференциальное уравнение первого порядка

у' = f (х, у). (1)

Тре6уется найти решение y=y(х) этого уравнения, удовлетворяющее начальному условию

у(х₀) == y₀ . (2)

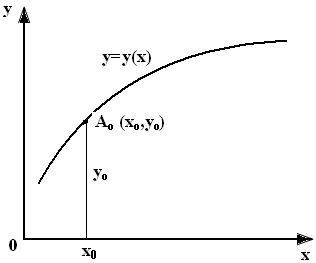
Такая задача называется задачей Коши. Геометрический смысл ее решения состоит в нахождении интегральной кривой у=у(х), проходящей через заданную точку А₀ (х₀,у₀) (рис. 1).

Существуют следующие постановки задачи Коши:

• дифференциальное уравнение первого порядка, разрешённое относительно производной:

y ' = f(x,y)

y(x₀) = y_0,

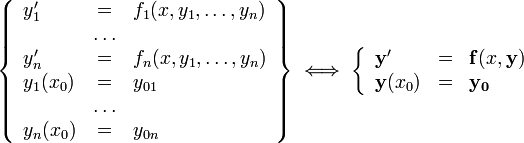
• система n дифференциальных уравнений первого порядка, разрешённая относительно производных (нормальная система n-го порядка):

• дифференциальное уравнение n-го порядка y⁽ⁿ⁾=f(x,y,y',…y^(n-1)), разрешённое относительно старшей производной y⁽ⁿ⁾:

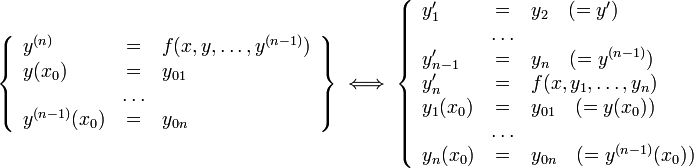
Численное решение задачи Коши состоит в нахождении значений y₁, y₂,...,у_n в точках х₁=х₀+h, х₂=х₀+2h,…, х_n=х_о+nh отрезка [a, b], где h - шаг интегрирования, х₀=а, х_n=b.

Рис. 1. График кривой у=у(х)	Рис. 2. Ломаная Эйлера

Нанеся точки (х_о,у_о), (х₁,у₁),...,(х_n,у_n) на координатную плоскость и соединив отрезками прямой, получим ломаную линию, называемую ломаной Эйлера, - приближенное изображение интегральной кривой (рис.2).

Самый простой и менее точный - метод Эйлера (метод первого порядка точности, расчетные формулы (4)). Наиболее распространенным является метод Рунге-Кутта (метод четвертого порядка точности, расчетные формулы (5)).

Последовательность вычислений по указанным методам следующая:

1. Разбиваем отрезок [а,b] на n равных частей точками х_i=х_о+ih (i = 1. 2. ..., n), где шаг h =(b-a)/n, х_о=а, х_n=b.

2. Находим решение уравнения, рассчитывая для каждого i (i=0,1,2,…,n) значения

y_i+1 = y_i + Δy_i, (3)

где Δy_i= k₁⁽ⁱ⁾ (4)

для метода Эйлера и

Δy_i=1/6(k₁⁽ⁱ⁾+2 k₂⁽ⁱ⁾+ 2k₃⁽ⁱ⁾ + k₄⁽ⁱ⁾) (5)

для метода Рунге-Кутта.

Коэффициенты k_j⁽ⁱ⁾, j=1,4 для выражений (4) и (5) определяются по следующим формулам:

k₁⁽ⁱ⁾=hf(x_i,y_i);

k₂⁽ⁱ⁾=hf(x_i+h/2, y_i+ k₁⁽ⁱ⁾/2);

k₃⁽ⁱ⁾=hf(x_i+h/2, y_i+ k₂⁽ⁱ⁾/2);

k₄⁽ⁱ⁾=hf(x_i+h, y_i+ k₃⁽ⁱ⁾).

Для выполнения вычислений по методу Рунге-Кутта вручную удобно пользоваться схемой, приведенной в табл. 33. Ориентировочную оценку погрешности метода Рунге-Кутта ε можно вычислить по формуле (6)

ε=|y_2h - y_h|/15. (6)

Метод Рунге-Кутта является одним из методов повышенной точности и, несмотря на свою трудоемкость, широко используется при численном решении, как дифференциальных уравнений, так и систем дифференциальных уравнений.

Среди встроенных функций SMath Studio для численного решения дифференциальных уравнений есть встроенная функция, реализующая метод Рунге – Кутта с постоянным фиксированным шагом. Она имеет вид: rkfixed( v,x₀,x_k,n,F). Здесь v - начальные условия, записанные в виде вектора, x₀, x_k – начальное и конечное значения аргумента, n- число шагов, F- правые части системы, записанные в виде вектора. Длина шага интегрирования определяется выражением h=(x_k-x₀)/n.

Как и большинство методов численного решения дифференциальных уравнений, метод Рунге – Кутта требует предварительного представления дифференциального уравнения n-го порядка в виде системы дифференциальных уравнений первого порядка:

Преобразование дифференциального уравнения в систему уравнений будет рассмотрен при решении примеров.

Отметим, что в последних версиях MathCad появилась функция odesolve(х, b) (ordinary differential equation solution – решение обыкновенного дифференциального уравнения), позволяющая решать уравнение без его преобразования. Здесь х – переменная интегрирования, b- верхняя граница изменения аргумента. Нижняя граница равна нулю.