3. 24. Анализ точности цифровых систем управления в установившемся режиме.
Пусть цифровая система управления служит для воспроизведения задающего воздействия v(t). При этом в идеальном случае надо обеспечить равенство управляемой величины у(t) и задающего воздействия. Практически реальная система решает эту задачу с ошибкой воспроизведения
. (86)
Для
того чтобы оценить, насколько хорошо
цифровая система воспроизводит
задающее
воздействие, надо найти величину этой
ошибки
.
Однако в рамках математической модели цифровой системы управления, ориентированной на дискретный фильтр, можно вычислить лишь управляемую последовательность
,
т.е. определить дискретные значения управляемой величины. Поэтому для оценки свойств системы с точки зрения воспроизведения сигнала v(t) приходится довольствоваться последовательностью ошибки
,
(87)
где
,
-
задающая последовательность. Очевидно,
что последовательность ошибки не дает
информацию о том, как изменяется ошибка
воспроизведения в промежутке между
моментами дискретизации, а следовательно,
не дает полного представления об этой
ошибке. Все же в тех случаях, когда период
дискретизации является небольшим по
сравнению с инерционностью объекта
управления, управляемая величина
изменяется плавно и путем интерполяции
последовательности ошибки можно получить
кривую
,
которая
будет достаточно точной оценкой ошибки
.
Однако
в
любом
случае
надо
помнить, что цель управления непрерывным
объектом заключается в обеспечений
малости ошибки
в
любой момент времени, а не только в
дискретные моменты
.
Если цифровая система является устойчивой, то последовательность ошибки
,
(88)
состоит
из переходной составляющей
,
которая с течением времени затухает,
т.е.
и
установившейся составляющей
,
которая служит для оценки точности
работы цифровой системы в установившемся
режиме и называется установившейся
ошибкой воспроизведения.
Разумеется, на самом деле установившейся
ошибкой является установившаяся
составлявшая ошибки
,
а не последовательность
.
Рассмотрим метод вычисления установившейся ошибка воспроизведения , полагая, что другие внешние воздействия, а именно шум измерения и возмущающее воздействие, отсутствуют.
3. 25. Метод, базирующийся на теореме о конечном значении z- преобразования.
Этот метод позволяет находить установившуюся ошибку при задающих воздействиях в виде степенной функции порядка l:
,
,
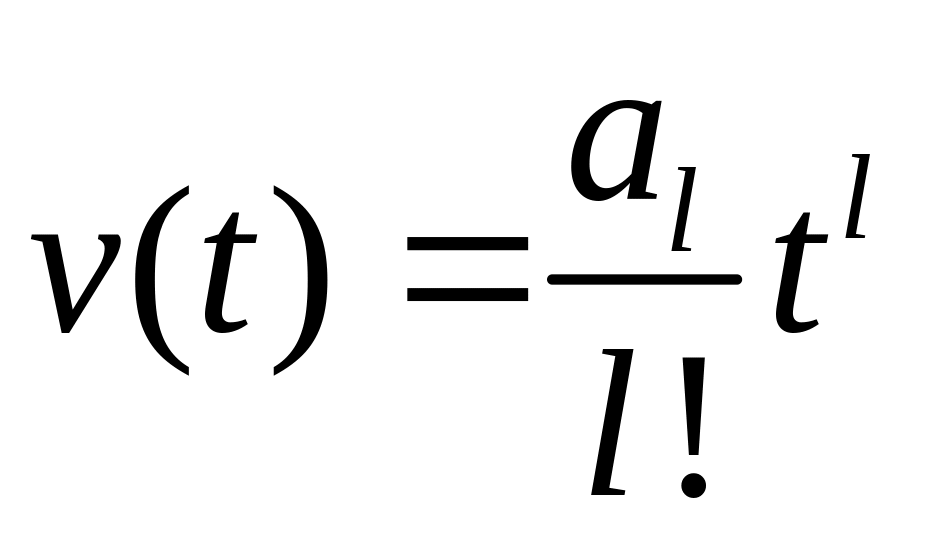(89)
При таком воздействии последовательность ошибки стремится к пределу, т.е.
,
так что установившаяся ошибка цифровой системы представляет собой последовательность равных между собой чисел (постоянную последовательность). Используя теорему о конечном значении, находим выражение
,
(90)
дающее возможность оценить установившуюся ошибку с помощью Z-преобразования
,
последовательности ошибки.
Ограничимся рассмотрением цифровой системы с единичной обратной связью, для которой
,
(91)
где
,
- Z-преобразование задающей последовательности.
Представляя передаточную функцию разомкнутой системы в стандартной форме, т. е. в виде
, ,
где - число дискретных интеграторов (диграторов), k - безразмерный коэффициент усиления, из (91) имеем
.
(92)
Заметим,
что
,
где
-
размерный коэффициент усиления.
Подставлял (92) в (90), получаем формулу
для установившегося значения ошибки
.
(93)
Используем (93) для двух частных случаев:
а)
пусть l=0,
так что в соответствие с (88) задающее
воздействие является постоянным сигналом
при
,
т. е.
,
.
При этом задающая последовательность
,
а ее Z-преобразование
.
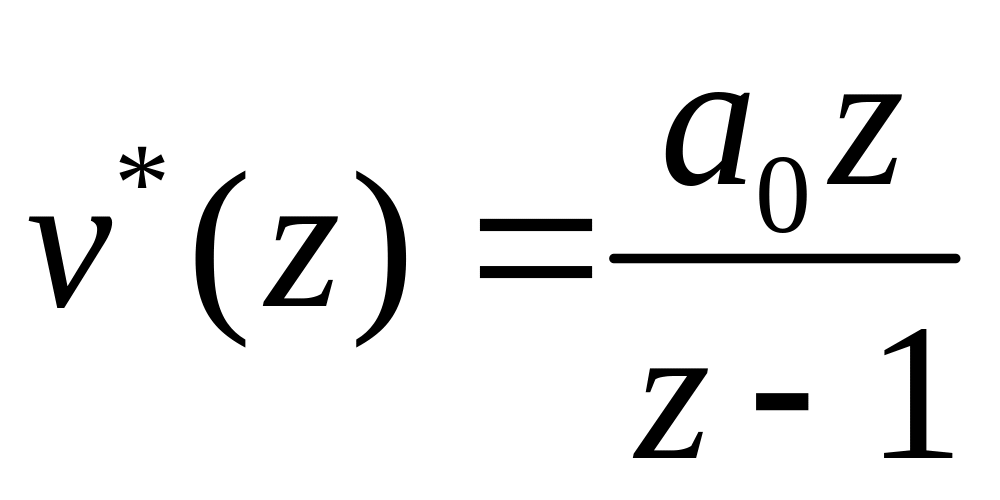Следовательно, формула (93) в этом случае принимает вид:
.
(93)
Установившаяся
ошибка при постоянном задающем воздействии
называется статической
ошибкой
и обозначается
.
Если
,
то
.
Система, для которой статическая ошибка отлична от нуля, называется статической.
Если
,
то
.
Система,
обеспечивающая безошибочное воспроизведение
постоянного задающего воздействия,
т.е. обеспечивающая равенство нуля
статической ошибки, называется
астатической
(нестатической). Таким образом, передаточная
функция
астатической
цифровой разомкнутой системы включает
в себя по меньшей мере один дигратор.
Число таких диграторов определяет
порядок астатизма цифровой системы с
единичной:
обратной связью. Если
,
то система обладает астатизмом первого
порядка; если
,
то система имеет астатизм второго
порядка и т.д.;
б)
пусть l=1,
при
этом согласно(88) задающее воздействие
представляет собой сигнал, изменяющийся
с постоянной скоростью
,
описываемый выражением
,
.
Этому сигналу соответствует задающая последовательность
,
Z-преобразование которой имеет вид
.
В
этом случае установившаяся ошибка (93),
называемая скоростной
ошибкой
или
ошибкой по скорости, определяется как
.
(94)
Если
система статическая (
),
то
.
Для системы с астатизмом первого порядка
(
)
скоростная ошибка
.
обратно
пропорциональна размерному коэффициенту
усиления
и не зависит от величины периода
дискретизации Т.
.Если же система обладает астатизмом
по крайней мере второго порядка (
),
ошибка
по скорости равна нулю.
В общем случае, когда задающее воздействие описывается степенной функцией порядка l, с помощью (92) можно установить, что
Число интеграторов в разомкнутой системе определяет класс задающих воздействий, для которых нет установившейся ошибки. Если разомкнутая система имеет интеграторов, то ошибка
в установившемся режиме будет равна нулю (при условии, что система асимптотически устойчива) для задающих воздействий, которые являются многочленами от i порядка, меньшего или равного (v-1).
Пример.
Рассмотрим разомкнутую систему
.
При этом z- преобразование ошибки замкнутой системы (рис. 25) определяется как
.
Предположим, что v - единичная ступенчатая функция. Так как замкнутая система устойчива, можно применить теорему о конечном значении, чтобы показать, что статическая ошибка равна нулю. Это легко сделать, положив z=1. Можно поступить иначе и воспользоваться тем, что разомкнутая система содержит один интегратор, т.е. полюс в точке +1.
Если v - сигнал, изменяющийся с постоянной скоростью, то установившаяся ошибка определяется соотношением:
.