Выбор постоянной времени слежения
Постоянная
времени слежения
является параметром антинакопления.
При
очень малых значениях постоянной
(большом значении коэффициента
дополнительной обратной связи
)
шум измерения сигнала
(t)
может повлечь за собой насыщение
выходного сигнала исполнительного
устройства, что приведет к случайному
уменьшению (сбросу) интегральной
составляющей. Слишком большое значение
замедляет реакцию системы (рис. 7).
Рекомендуется
выбирать значение
,
используя соотношения
или
.
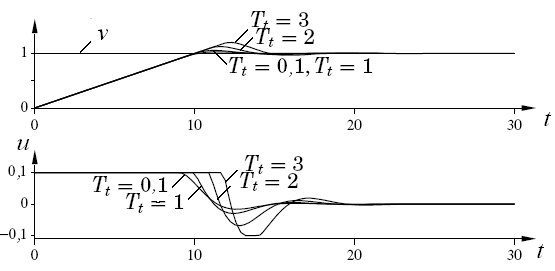
Рис. 7
8. Синтез нелинейной следящей системы методом линеаризации обратной связью
Сущность метода: линеаризация обратной связью (feedback linearization) нелинейного ОУ полностью или частично так, чтобы можно было использовать линейную теорию управления.
- Такой метод является одним из методов проектирования нелинейных систем управления.
- Основная идея этого метода: алгебраическим способом преобразовать модель динамического нелинейного ОУ коренным образом отличается от классической линеаризации (так называемой тейлоровской или якобианской линеаризации) тем, что используется обратная связь по состоянию, а не линейная аппроксимация динамики нелинейного объекта.
- Технологию линеаризации можно трактовать как метод преобразования исходной нелинейной модели ОУ в эквивалентную линейную модель более простого вида.
Идея линеаризации обратной связью сократить (аннулировать) нелинейности модели ОУ и придать системе управления желаемые линейные динамические свойства.
Линеаризация обратной связью применима к классу нелинейных диамических ОУ, допускающих описание с помощью канонической формы управляемости.
Рассмотрим ОУ, описываемый уравнением движения в канонической (аффинной) форме
y(t)
=x(t),
которое можно представить в переменных состояния как
,
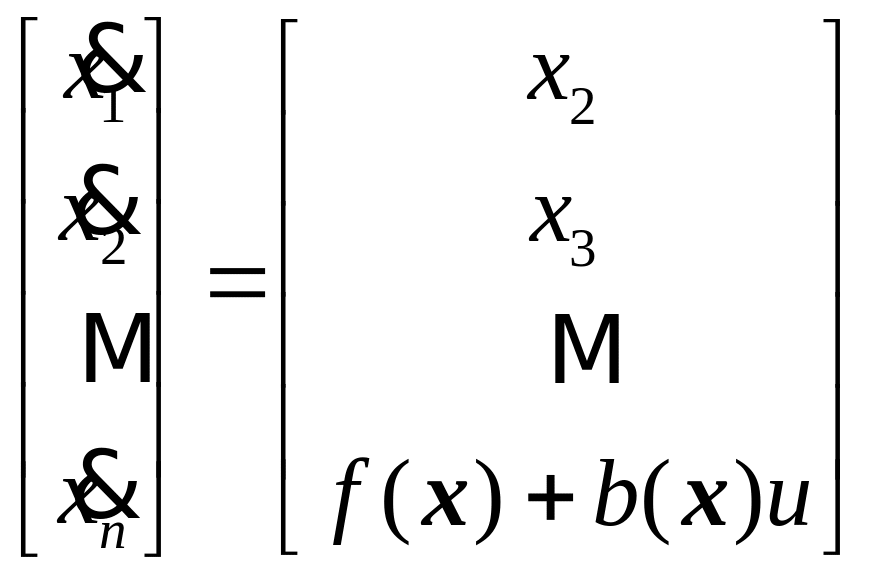(1)
где
=
вектор
состояния,
f и b нелинейные функции времени, u и y скалярные вход и выход ОУ соответственно.
Цель
управления:
принудить вектор состояния
отслеживать конкретную желаемую
траекторию
,
другими словами, заставить
y(t)
следить за
изменениями желаемого сигнала
.
Если мы определим векторную ошибку
слежения как
,
то целью управления можно считать
проектирование закона управления,
который обеспечивает
при
.
Для этого объекта, используя управляющее
воздействие в виде
,
(2)
другими словами, используя линеаризацию обратной связью, можно сократить нелинейности и найти уравнение вход-выход в форме n-кратного интегратора
.
(3)
Тогда
принимая в качестве
,
которое называют «эквивалентным
управлением (входом)»
,
(4)
где
коэффициенты вектора
выбираются так, чтобы характеристическое
уравнение
имело все корни, расположенные в ЛПП,
, закон управления (2) приводит к
асимптотически устойчивой замкнутой
системе, описываемой уравнением для
ошибки
:
,
(5)
из которого следует, что
при
.
Если
= 0 (рассматривается
задача регулирования), то эквивалентное
управление принимает вид
и тогда закон управления (2) преобразует (1) в уравнение
,
которое обеспечивает удовлетворительное поведение замкнутой системы, описываемой уравнением (1), по меньшей мере, обеспечивает асимптотическую устойчивость замкнутой системы.
Замечание. Если динамика нелинейного объекта представлена не в канонической форме управляемости, надо, используя алгебраические преобразования, вначале привести модель ОУ к канонической форме управляемости, а затем использоваь вышерассмотренную методику проектирования обратной связи по состоянию.