3. Основное уравнение метода гармонического баланса.
Если в системе, изображенной на рис. 3,
гармонически
линеаризовать нелинейный элемент,
заменив его эквивалентной передаточной
функцией
,
то она становится линейной (гармонически
линеаризованной системой) (рис. 6).
Рис. 6
Следовательно, в этом случае для анализа свойств системы можно применять методы линейной теории управления.
Как
известно, в линейной системе (при
отсутствии синусоидального сигнала на
входе) незатухающие колебания будут
возникать лишь в том случае, когда она
находится на границе устойчивости.
Таким образом, для определения
автоколебаний в исходной системе (см.
рис. 3) необходимо рассмотреть условие
границы устойчивости линеаризованной
системы. В соответствии с критерием
Найквиста в этой ситуации амплитудно-фазовая
характеристика разомкнутой системы
должна проходить через точку
,
т. е.
.
Учитывая, что
,
запишем условие границы устойчивости в виде
.
(17)
Это уравнение и представляет собой основное уравнение метода гармонического баланса, из которого можно определить параметры автоколебаний. Если (17) не имеет положительных вещественных решений относительно A и , то автоколебательный режим в нелинейной системе не возникает.
Для решения основного уравнения метода гармонического баланса были предложены различные способы, из которых мы рассмотрим лишь способ Гольдфарба
4. Способ Гольдфарба.
Решение основного уравнения метода гармонического баланса (17) относительно амплитуды и частоты автоколебаний можно получить графически.
В способе Гольдфарба, прежде всего, предлагается разрешить основное уравнение относительно частотной характеристики линейной части системы:
.
(18)
Затем
на комплексной плоскости строятся
амплитудно-фазовая характеристика
и
характеристика, соответствующая
нелинейному элементу, т. е. обратная
частотная характеристика нелинейного
элемента,
.
(19)
Если эти две характеристики не пересекаются, то периодических процессов в нелинейной системе не возникает.
При наличии пересечений частота автоколебаний определяется по частотной характеристике линейной части системы , а амплитуда - по характеристике нелинейного элемента в точке пересечения.
Поскольку в общем случае точек пересечения и характеристики нелинейного элемента (19) может быть несколько, в системе могут возникать соответствующие им периодические процессы различных амплитуды и частоты. Причем часть из них будут устойчивыми, а часть - неустойчивыми.
Устойчивость найденного колебательного режима позволяет оценить следующее правило (оно не является строго обоснованным, но зачастую оказывается достаточным). Если при движении по обратной частотной характеристике нелинейного элемента в сторону увеличения амплитуды происходит пересечение амплитудно-фазовой характеристики линейной части «изнутри наружу», то этой точке пересечения соответствуют устойчивые колебания (автоколебания). В противном случае колебания будут неустойчивыми.
На
рис. 8 характеристики
и
пересекаются
в двух точках. Это означает, что в системе
могут возникать два
вида
колебаний.
Рис. 8
Причем
первой точке пересечения соответствуют
устойчивые колебания (автоколебания)
с амплитудой A1
и
частотой
,
а второй точке - неустойчивые.
Пример.
Определить
параметры колебаний и проверить их
устойчивость для системы, изображенной
на рис. 6. Здесь нелинейный элемент
представляет собой идеальное реле (см.
рис. 5) с уровнем ограничения
,
а
передаточная функция линейной части
следующая:
.
П
олучим
выражение для амплитудно-фазовой
характеристики (рис. 9)
в
виде
,
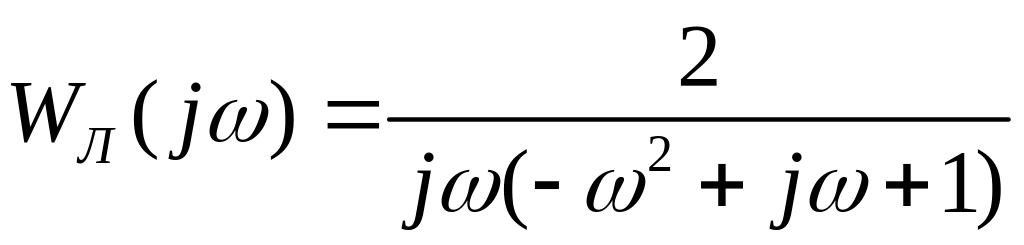или
.
Запишем выражение для частотной характеристики нелинейного элемента, а затем построим годограф (рис. 9)
.
Как видим, эти характеристики пересекаются в одной точке, которая соответствует автоколебаниям. Для определения их параметров найдем координаты точки пересечения, для чего приравняем нулю мнимую часть : Рис. 9
.
Отсюда
следует, что
.
При найденном значении частоты получим
.
Из условия
,
определим
амплитуду автоколебаний:
.