Пассивность
Пассивность является важным свойством и важным инструментом в анализе устойчивости и проектировании нелинейных систем управления. Идея пассивности берет свое начало в теории электрических цепей. Рассмотрим двухполюсник, представленный на рис. 1.
Рис. 1.
Ток,
протекающий через это устройство,
обозначен как y
и приложенное к этому устройству
напряжение обозначено как u.
Предположим, что u
и y
связаны между собой с помощью полного
сопротивления (импенданса), обозначенного
как z,
так что u=zy.
Заметим, если uy
0
, то известно, что часть энергии, подводимой
к цепи, поглощается ее элементами (в
первую очередь резисторами) и мы говорим
о том, что эта цепь яляется пассивной.
Если же uy<0,
то цепь питает энергией другие цепи, и
она является активным элементом (содержит
внутренние источники энергии).
Простая RC-цепь мотивирует последующее обсуждение данного вопроса (рис. 2). В этом цепи мы примем ток от источника как состояние x цепи и в тоже время как ее выходной сигнал y, т.е. y=x. Тогда уравнение остояния для цепи можно
Рис. 2
записать в виде
.
Отсюда
Цепь называется пассивной, если энергия, полученная цепью извне, больше, чем энергия, накопленная внутри ее, т.е.
Здесь слагаемое в левой части неравенства есть энергия, полученная цепью от внешнего источника, а разность в правой части неравенства есть энергия, запасенная (сохраненная, накопленная) цепью, и называется функцией запаса. Если мы найдем производную от обеих частей неравенства, то получим, что мощность сигнала, полученного цепью,
для всех t. Функция в правой части последнего неравенства называется функцией расхода.
Идея
Ляпунова:
Запасенная (сохраненная) энергия в
автономной системе с течением времени
уменьшается, так что
,
в силу
.
Идея
пассивности:
Увеличение сохраняемой энергии в
неавтономной системе ограничено внешней
энергией, так что
,
в силу
,
где
внешняя мощность.
Естественно, что увеличение сохраняемой
энергии может происходить благодаря
ненулевому входному воздействию
,
а не за счет внутренних источников
энергии, чем объясняется название
пассивная
система.
В нашем примере энергия, накопленная емкостью, следовательно, и цепью,
.
Отсюда
или
.
Первое
слагаемое правой части есть мощность,
полученная RC
цепью от внешнего источника, и второе
слагаемое есть мощность, поглощенная
резистором. Ясно, что второе слагаемое
отрицательно, поэтому
,
в силу чего эта RC
цепь является пассивной.
Прямой метод Ляпунова дает возможность судить об устойчивости состояний равновесия лишь автономных систем, т.е. об устойчивости по начальным условиям. Стремление распространить методику Ляпунова на неавтононые системы, другими словами, на системы с неравными нулю входными сигналами и привело к понятию пассивности нелинейных/линейных динамических систем управления. Распространим концепцию, обсужденную для RC цепей, на нелинейные динамические системы, описываемые в переменных состояния следующими уравнениями
где f нелинейная вектор-функция, преобразующая n- вектор состояния и r –вектор входа (управления), является локально липшицевой (непрерывной) функцией, удовлетворяющей условию f(0,0)=0, и h нелинейная непрерывная вектор-функция, преобразующая u и x в l-вектор выхода, причем h(0,0)=0.
Определение: Система, описываемая уравнениями
называется
пассивной, если существует скалярная
положительно определенная симметричная
функция
(называемая
функцией накопления или сохранения)
такая, что
.
(*)
Кроме того,
Система есть система без потерь, если
.Система есть строго пассивной по входу, если
для
некоторой функции
,
причем
>
0.
Система есть строго пассивной по выходу, если
для
некоторой функции
,
причем
>
0.
Система есть строго пассивной, если
(***)
для
некоторой положительно определенной
функции
.
Свойство пассивности можно трактовать так: пассивная система не может накопить больше знергии, чем ею получено от внешнего источника.
Пример.
Пассивность статической нелинейности,
описываемой нелинейным алгебраическим
уравнением
.
Такая нелинейность, расположенная в
первом и третьем квадрантах (рис. ниже)
является пассивной, если ось u
включена в определение функции и строго
пассивной в противном случае. Это можно
показать, используя (*) и учитывая, что
по определению функция накопления
для
этого элемента равна нулю, так что
энергия рассеивается все время до тех
пор, пока или u
или
не станут раными нулю. Отсюда
.
Пример. Рассмотрим линейную асимптотически устойчивую систему
.
Предположим, к тому же существуют положительно определенные симметричные матрицы P, Q такие, что
.
(**)
Выберем
Тогда
Отсюда система является строго пассивной. Из леммы Калмана-Якубовича-Попова следует, что если условия (**) имеют место, то ПФ системы
удовлетворяют условию
,
где
{.}
означает вещественную часть.
Таким
образом, линейная
асимптотически устойчивая система с
ПФ
является
пассивной системой, если ее вещественная
частотная характеритика является
положительной для всех положительных
частот,
,
т.е.
АФХ
для любых значений
лежит в правой
половине комплексной плоскости, точнее
в четвертом квадранте комплексной
плоскости (рис. ниже). Передаточная
функция
системы, удовлетворяющей этому свойству,
имеет относительную степень (разность
порядков знаменателя и числителя) равную
единице, и называется строго
вещественно-положительной.
Поэтому лемму Калмана-Якубовича-Попова
именуют как лемму о вещественной
положительности.
Из
этой леммы, касающейся фазочастотной
характеристики линейной динамической
пассивной системы, следует вывод,
согласно которому значения фазочастотной
характеристики такой системы лежат в
пределах от 0 до
.
Существует
важная и полезная связь между пассивностью
и устойчивостью типа вход- выход и
устойчивостью по Ляпунову. Эта связь
хорошо известна в теории нелинейных
систем. В отсутствие входного сигнала
(u=0)
из выражения (***) получаем, что
.
Если кроме того функция запаса
положительно
определена и неограниченно возрастает,
то по теореме Ляпунова автономная
система
глобально асиптотически устойчива в
точке x=0,
т.е.
энергия пассивной системы убывает до
нуля.
Теперь приведем теорему, касающуся устойчивости типа ограниченный вход-ограниченнй выход.
Теорема: Рассмотрим систему, описываемую уравнениями
где
f
локально липшицевая (f(0,0)=0)
и h
непрерывная (h(0,0)=0)
нелинейные функции. Если эта система
является строго пассивной по выходу с
,
то она является L2
устойчивой по входу с конечным L2
-
коэффициентом
усиления
,
который меньше чем или равен 1/
,т.е.
.
Доказательство: Производную от функции накопления можно дополнить до полного квадрата
.
Действительно,
с учетом
,
Отсюда
с учетом
(здесь
)
или
.
Интегрируя в пределах от нуля до t, получаем
.
Так как V(x)>0, то устремляя t к бесконечности и вспоминая определение второй нормы, приходим к неравенству
,
из которого следует, что
.
Пример. Объект управления: масса- демпфер-пружина.
Математическая модель объекта с учетом приложенной к массе силе u=F имеет вид дифференциального уравнения
.
(*)
Полная механическая энергия = кинетическая энергия + потенциальная энергия, накопленная объектом, как показано ранее,
.
(**)
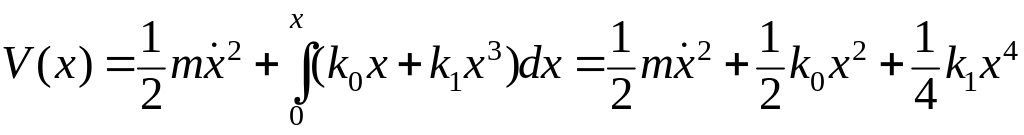Дифференцируя
первое равенство в выражении (**) и
используя (*), а таже принимая в качестве
выходного сигнала первую производную
от перемещения массы, т.е.
,
получаем
.
(***)
Как видим, данная система является строго пассивной по выходу, т.к.
.
При этом система является L2 устойчивой по входу от u к y с конечным коэффициентом усиления , который меньше чем или равен 1/ ,
,
где
.
Заметим,
что, если нас интересует устойчивость
типа «ограниченный вход-ограниченный
выход», то условие пассивности (*),
представленное в интегральной форме
,
можно записать иначе. Принимая начальное
состояние, равным нулю, и предполагая,
что существует
с
,
причем
,
получаем
.
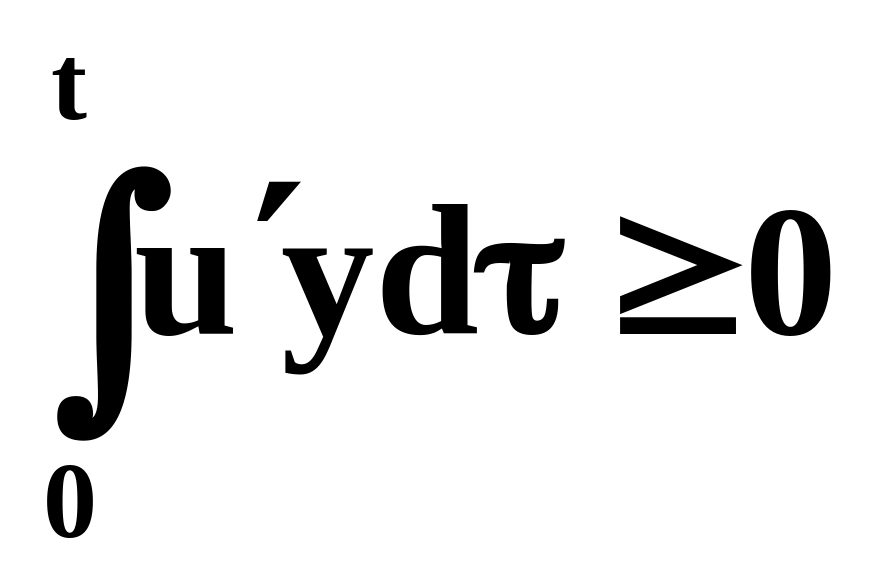При этом систему S называют пассивной от входа u к выходу y , если
для всех u и t>0 и строго пассивной от входа u к выходу y , если
.
