Лекция 19

Рассмотрим два свойства амплитудно-фазовой характеристики цифровой системы:

I. Амплитудно-фазовая характеристика цифровой системы представляет собой периодическую функцию относительной частоты с периодом , т.е.

, (55)

Действительно,

,

так как

,

В связи с периодичностью для полного суждения о ее поведении достаточно знать, какие значения она принимает при изменении в любом диапазоне шириной . Обычно используют диапазон низких частот : от до . Периодичность порождает так называемый стробоскопический эффект, который заключается в том, что цифровая система имеет одинаковую реакцию как на частоту , так и на частоту . Это обстоятельство еще раз свидетельствует о поглощении частот, вызванной дискретизацией.

Годограф , построенный на комплексной плоскости при изменении от - до , называется диаграммой Найквиста. Кстати, относительная частота измеряется как [рад/выборку], где под выборкой понимается число периодов дискретизации Т, укладывающееся в период непрерывного сигнала .

2. При изменении знака у частоты в аргументе амплитудно-фазовой характеристики получаем комплексно-сопряженное выражение, т. е.

, (56)

где - символ комплексно-сопряженного выражения.

Действительно, представляя в алгебраической форме

,

где

, ,

и учитывая, что

,

находим

,

откуда вытекает равенство (56). Таким образом, если известно выражение для положительных частот , то нетрудно найти значения этой характеристики и для отрицательных частот . Это свойство позволяет в два раза уменьшить диапазон изменения частоты при исследовании поведения , т.е. вместо диапазона дает возможность ограничиться диапазоном .

Амплитудно-фазовой характеристикой цифровой системы называется не только само выражение , но и годограф построенный, на комплексной плоскости при изменении от 0 до .

На рис. 19 представлены диаграммы Найквиста цифровой и соответствующей непрерывной систем, причем диаграмма цифровой системы построена при изменении относительной частоты от до .

Опустить

Если u(k) = sin( k), то имеем

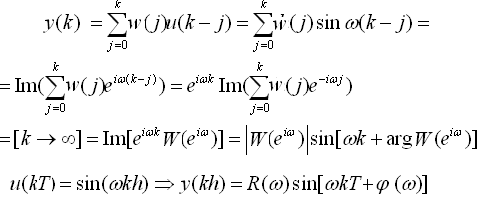
Читать

Для исследования цифровых систем используются также логарифмические частотные характеристики:

• амплитудная

,

• фазовая

,

построенные в логарифмическом масштабе частот .

На рис. 20 изображены вкачестве примера логарифмические частотные характеристики непрерывной системы с передаточной функцией 1/(р²+1.4p+1) (пунктир) и соответствующей цифровой системы (сплошная).

3. 20. Структурная схема цифровой системы с обратной связью.

Достаточно полной математической моделью линейной цифровой системы управления с обратной связью (замкнутой цифровой системы) является разностное, уравнение, связывающее между собой управляемую последовательность с внешними воздействиями; для получения такого уравнения, как и в теории непрерывных систем, удобно использовать метод, связанный с построением и последующим преобразованием структурных схем цифровых систем.

Рассмотрим стандартную функциональную схему цифровой системы управления, изображенную на рис. 21.

Мультиплексор

Два измеряемых непрерывных сигнала - задающее воздействие и наблюдаемая величина - сканируются, т.е. подключаются поочередно к АЦП, с помощью мультиплексора. Применение мультиплексора позволяет избежать необходимости включения в схему двух АЦП для преобразования каждого из сигналов и в отдельности, что с экономической точки зрения в ряде случаев целесообразно. Рассматривая АЦП как ключ (дискретизатор), можно считать, что его функция заключается в том, чтобы получить задающую

,

и наблюдаемую

,

последовательности. Разумеется, АЦП преобразует сигналы и в цифровую форму не в одно и то же время . Однако, принимая во внимание, что время преобразования занимает ничтожную часть периода дискретизации T, задержками в выдаче задающей и наблюдаемой последовательностей можно пренебречь и считать, что они появляются на выходе АЦП в моменты замыкания ключа.

Программа работы ЦВМ определяется выбранным законом управления. Предположим, что в рассматриваемом случае используется линейный закон управления с прямой и обратной связью. При этом ЦВМ осуществляет следующие операции:

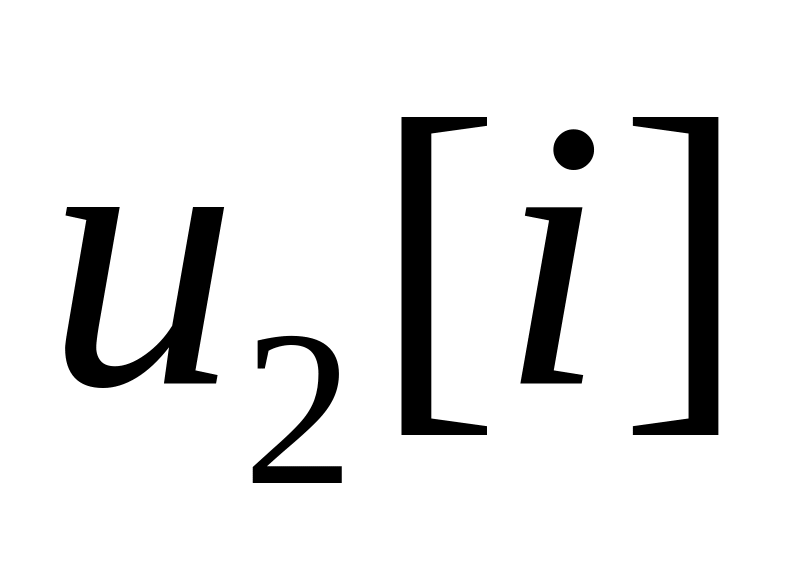1. Преобразует задающую последовательность в последовательность прямой связи в соответствии с заданным алгоритмом. Этому алгоритму соответствует линейное разностное уравнение, связывающее последовательности и . Следовательно, можно считать, что рассматриваемая операция осуществляется дискретным фильтром прямой связи , описываемым упомянутым разностным уравнением.

2. преобразует наблюдаемую последовательность 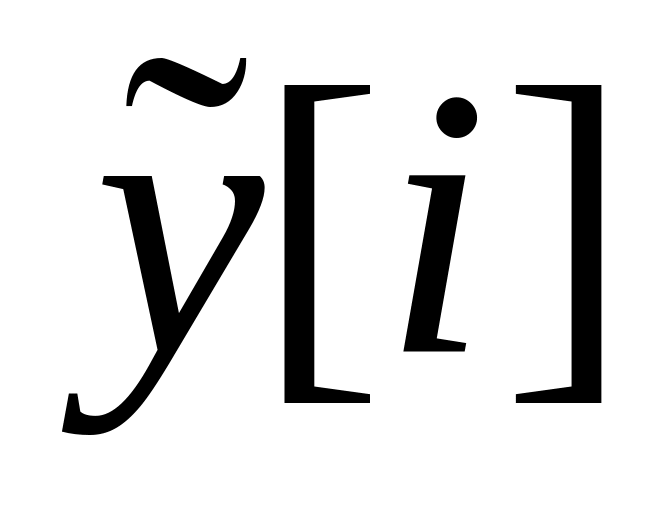в последовательность обратной связи в соответствии с другим заданным алгоритмом, который в общем случае отличается от алгоритма преобразования в . При этом последовательности и оказываются связанными линейным разностным уравнением, что можно трактовать как преобразование последовательности в последовательность с помощью дискретного фильтра обратной связи ;

3. вычисляет управляющую последовательность

, (57)

как разность последовательностей прямой и обратной связи.

ЦАП, преобразующий управляющую последовательность и[i] в управляемый сигнал, можно рассматривать, как фиксатор нулевого порядка Ф. Пусть объект управления ОУ характеризуется передаточной функцией , связывающей преобразования Лапласа выходного сигнала объекта и управляющего воздействия . Управляемую величину

, (58)

можно рассматривать как сумму сигнала и возмущающего воздействия , приведенного к выходу объекта управления.

Будем считать, что в процессе измерения управляемая величина искажается шумом измерения так, что наблюдаемый сигнал

. (59)

Для получения математической модели цифровой системы управления осуществим дискретизацию сигналов и . При этом, используя (58) и (59), получаем уравнения связи

, (60)

где

- управляемая последовательность,

- последовательность выхода ОУ,

- возмущающая последовательность;

, (61)

где - наблюдаемая последовательность,

- последовательность шума измерения.

Заменяя ЦАП фиксатором и вводя фиктивные ключи (дискретизаторы), преобразующие соответственно в , переходим от схемы (рис.21) к блок-схеме, показанной на рис. 22.

Как видно из рис. 22, модель цифровой системы управления, ориентированная на дискретный фильтр, состоит из соединения трех дискретных фильтров: , и дискретного фильтра, эквивалентного последовательному соединению фиксатора, объекта и ключа. Так как по условию известны уравнения фильтров и , нетрудно найти соответствующие операторные передаточные функции этих фильтров и . Операторная передаточная функция объекта, управляемого от ЦВМ, может быть найдена по передаточной функции :

. (30)

Отбрасывая ключи и считая внешними воздействиями цифровой системы управления последовательности , а ее выходом последовательность , приходим к структурной схеме (рис. 23),

которая отображает разностные уравнения дискретных фильтров

,

, (62)

,

и уравнения связи (57), (60) и (61) во временной области. Используя Z-преобразование, записываем уравнения (57), (59) - (62) в изображениях. При этом получаем:

I) передаточную функцию объекта, управляемого от ЦВМ,

. (63)

2) передаточную функцию прямой связи

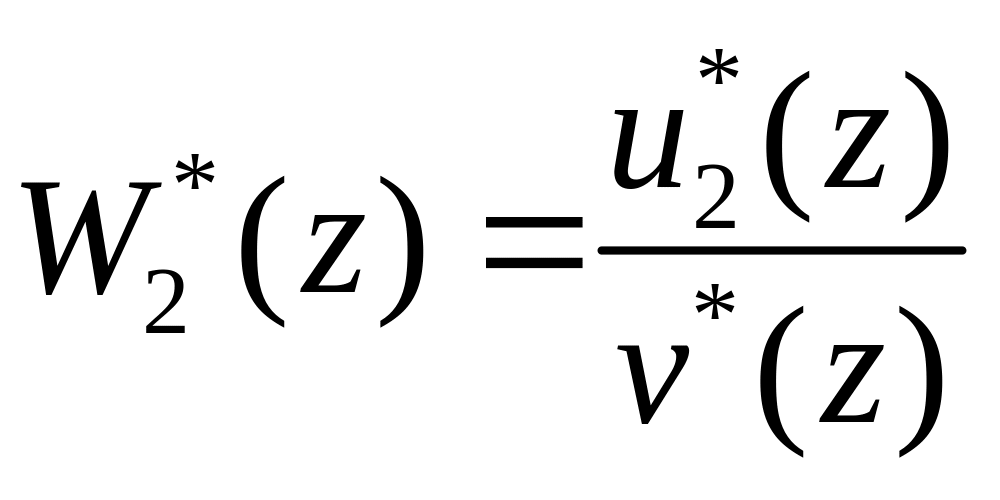. (64)

3) передаточную функцию обратной связи

. (65)

а также уравнения связи

(66)

По уравнениям (62) - (65) строим структурную схему цифровой системы с обратной связью (рис. 24), отображающую уравнения дискретных фильтров и уравнения связи в комплексной области Z.

В настоящее время структуру системы, представленной на рис. 24, называют структурой с двумя степенями свободы, имея в виду два дискретных фильтра, входящих в управляющее устройство.

Как видим, рассмотрение всех сигналов как числовых последовательностей и введение соответствующих передаточных функций для алгоритмов ЦВМ и объекта управления с ЦАП и АЦП позволили получить структурную схему, аналогичную обычной структурной схеме непрерывной системы. Так же, как и для непрерывных систем, каждый дискретный фильтр подобно непрерывному звену изображается прямоугольником и описывается алгебраическим уравнением. Разница заключается лишь в том, что непрерывные звенья описываются уравнениями в преобразованиях Лапласа, а фильтры - уравнениями в Z – изображениях.

Следовательно, все правила преобразования структурных схем непрерывных систем применимы для упрощения и свертывания структурных схем цифровых систем.

Так, например, если используется закон управления по ошибке, то алгоритмы преобразования сигналов v[i] и y[i] совпадают. При этом

.

Тогда, перенося элемент суммирования 1 (рис. 24) на вход фильтра с передаточной функцией и используя соответствующее правило преобразования структурных схем непрерывных систем, приходим к структурной схеме цифровой системы управления с единичной обратной связью (рис. 25).

На этой схеме:

есть Z-преобразование последовательности ошибки управления

,

а

,

есть Z-преобразование последовательности шума измерения ошибки управления . Дело в том, что в цифровых системах с единичной обратной связью, как правило, измеряют не v(t) и y(t), а их разность - ошибку управления

,

и этот процесс сопровождается шумом измерения , так что наблюдается сигнал ошибки