§1. Диференціювання

Література: §21; гл.5, § 1-2.

1. Поняття похідної

Поняття похідної – фундаментальне поняття математичного аналізу, за допомогою якого досліджуються процеси і явища в природничих, соціальних та економічних науках. Зокрема, при застосуванні таких економічних понять, як попит, витрати виробництва, національний прибуток тощо, часто доводиться визначати швидкість зміни значень відповідних величин. Розв’язання таких задач ґрунтується на методах диференціального числення. Тому вивченню похідної слід приділити особливу увагу.

Нехай функція y=f(x) визначена і неперервна в деякому проміжку і нехай довільне значення і точка належать цьому проміжку. Знайдемо відповідний приріст функції Тоді відношення характеризує середню швидкість зміни функції на відрізку Щоб дістати більш точну характеристику зміни функції, розглянемо Якщо ця границя існує, то вона характеризує швидкість зміни функції в точці

Означення. Похідною функції в точці x називається границя відношення приросту функції в цій точці до приросту аргументу, коли приріст аргументу прямує до нуля.

За означенням

(1)

Позначають так:

Термін «похідна» запровадив французький математик Лагранж. Якщо в точці то якщо ж ця границя не існує, то не існує в цій точці і похідної.

Якщо границя (1) існує в кожній точці деякого проміжку, то похідна є функцією від в цьому проміжку. Для даного фіксованого значення аргументу похідна є певним числом.

Функцію, яка має скінченну похідну в точці , називають диференційовною в точці . Функція називається диференційовною в інтервалі, якщо вона диференційовна в кожній точці цього інтервалу. Операція знаходження похідної від функції називається диференціюванням цієї функції.

ТЕОРЕМА. Якщо функція диференційовна в точці , то вона неперервна в цій точці.

Обернене твердження, взагалі кажучи, не має місця, тобто з 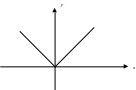неперервності функції в точці не випливає її диференційовність. Так, наприклад, функція неперервна в точці але вона не має в цій точці похідної.

Отже, неперервність функції в точці є лише необхідною умовою її диференційовності в цій точці.

Геометричний зміст похідної. Значення похідної в точці дорівнює кутовому коефіцієнту дотичної, проведеної до графіка цієї функції у точці з абсцисою Отже, де – кут нахилу дотичної.

Механічний зміст похідної. Якщо функція описує закон прямолінійного руху матеріальної точки, де – шлях, – час, то швидкість в даний момент часу – це похідна від пройденого шляху

Узагальнюючи, можна сказати так: якщо функція описує деякий фізичний процес, то похідна є швидкістю зміни цього процесу. В цьому полягає фізичний зміст похідної.

Економічний зміст похідної пояснимо на прикладі. Якщо позначити через прибуток від продажу одиниць товару, то границя називається маргінальним (граничним) прибутком.

1.2. Безпосереднє диференціювання

Якщо похідна даної функції знаходиться згідно з означенням (за формулою (1)), тобто шляхом послідовного визначення і то такий спосіб знаходження похідної називається безпосереднім диференціюванням.

Приклад 1. Користуючись способом безпосереднього диференціювання, знайти похідну функції Обчислити

Розв’язання. При значенні аргументу, що дорівнює , маємо При значенні аргументу, що дорівнює , маємо Знаходимо приріст функції:

Складаємо відношення

Знаходимо границю відношення при а саме

Приклад 2. Виходячи з означення похідної, знайти похідну функції

Розв’язання. Знаходимо приріст функції

Складаємо відношення Таким чином,