8 Послiдовний резонансний контур

8.1 Визначення та умови резонансу

Коливальний контур  електричне коло, в якому можливi коливання вiльної складової струму. Резонансний контур  електричне коло, в якому має мiсце явище резонансу (напруг чи струмiв).

Послiдовний резонансний контур  резонансний контур, що складається з iндуктивного та ємнiсного елементiв, злучених послiдовно (рис.8.1а,б). На схемi (рис.8.1в) R, L, C  первиннi параметри контуру, причому , де  активний опiр котушки iндуктивностi,  опiр витiкання конденсатора, перерахований у послiдовне з’єднання,  опiр проводiв (втрат). Щоб визначити поняття резонансу, знайдемо струм у колi (рис.8.1в):

,

де  реактивний опiр контуру.

Запишемо комплексне дiюче значення струму в показниковiй формi:

,

де  повний опiр контуру.

Отже, резонанс  це явище в електричному колi, що має дiлянки з iндуктивним та ємнiсними елементами, за якого рiзниця фаз напруги i струму на входi кола дорiвнює нулю. З цього випливає, що повний опiр контуру при резонансі має бути активним, а реактивний опiр контуру дорiвнюватиме нулю.

а) б) в)

Рисунок 8.1

Отже, якщо у загальному випадку слушнi спiввiдношення

; , то при резонансi:

1)  це умова амплітудного резонансу;

2) ; ;  умова виникнення фазового резонансу.

8.2 Вториннi параметри послiдовного резонансного контуру

1. Резонансна частота  частота струму (напруги) пiд час резонансу в колi. Позначається i визначається, виходячи з умови резонансу X = 0; : ; .

Значенню циклiчної частоти вiдповiдає резонансна довжина хвилi:

, ,

де c  швидкiсть поширення електромагнiтних хвиль.

2. Характеристичний (хвильовий) опiр контуру  опiр кожного з реактивних елементiв при резонансi: .

3. Добротнiсть  вiдношення характеристичного опору до активного опору контуру: , де d  загасання  величина, обернена до добротностi, яка характеризує iнтенсивнiсть загасання коливань у контурi.

Добротнiсть характеризує тривалiсть власних коливань у контурi.

4. Повний опiр  модуль вхiдного комплексного опору контуру Z .

,

де  модуль Z;

 аргумент Z.

5. Фазова характеристика  залежнiсть аргумента вхiдного опору послiдовного контуру вiд частоти (рис.8.2а): .

6. Резонансна крива струму  залежнiсть модуля комплексного дiючого (амплiтудного) значення струму вiд частоти (рис.8.2б): .

На частотi резонансу слушні вирази: , .

8.3 Векторна діаграма напруг при резонансі

Запишемо для послiдовного резонансного контуру рiвняння за другим законом Кiрхгофа: .

За умови резонансу ( ), ,

де  напруга на опорi R ;  напруга на iндуктивностi;  напруга на ємностi.

На рис.8.2в зображено векторну дiаграму струму та напруг при резонансi. Як видно з рисунку, виконуються спiввiдношення:

1) напруга на опорi R збiгається за фазою зi струмом I, а модуль дорiвнює значенню E; напруги на реактивних елементах рiвні між собою за модулем та протилежнi за напрямком;

2) за абсолютною величиною напруги на реактивних елементах послiдовного резонансного контуру в Q разiв перевищують значення ЕРС, яка дiє на входi: . Отже, у послiдовному контурi спостерiгається резонанс напруг.

Резонанс напруг  явище резонансу на дiлянцi електричного кола, до якого входять послiдовно злученi iндуктивний та ємнiсний елементи.

а) б) в)

Рисунок 8.2

8.4 Резонансна крива струму. Абсолютна, вiдносна

та узагальнена розстройки

Кривi залежностi модуля комплексного амплітудного (діючого) значення струму (напруги) вiд частоти генератора називаються резонансними кривими. Рiвняння резонансної кривої струму має вигляд:

. (8.1)

Рiвняння (8.1) можна записати iнакше: .

Подiливши цей вираз на резонансне значення струму , матимемо нормовану резонансну криву струму:

. (8.2)

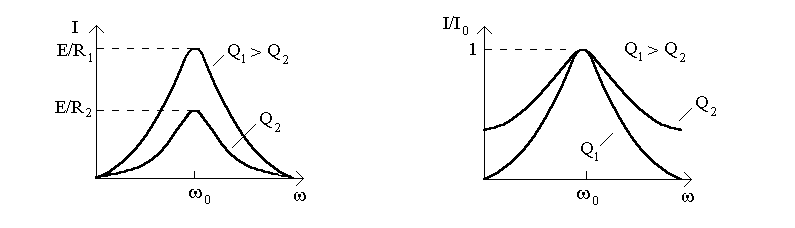
На рис.8.3а,б показано резонанснi кривi струмiв вiдповiдно до виразiв (8.1) та (8.2) для рiзних значень добротностi .

Розраховуючи в радіотехнічних пристроях резонансні контури, до-слiджують їх поведiнку головним чином в областi частот, близьких до резонансної частоти , тобто коли частота генератора дорiвнює:

; ,

де  абсолютна розстройка, яка є малою величиною порiвняно з резонансною частотою. Розстройка може бути як додатною , так i вiд'ємною ( , ).

Вiдношення називається вiдносною розстройкою. Величина називається узагальненою розстройкою. З урахуванням введених позначень формула (8.2) буде такою:

. (8.3)

а) б)

Рисунок 8.3

Знайдемо формули для розрахунку узагальненої розстройки:

Враховуючи, що , отримуємо формулу: .

Але для частот, близьких до резонансної частоти контуру , виконуються такi приблизнi спiввiдношення: ; .

Тодi .

Отже, кiнцева приблизна формула для знаходження така: .

Резонансна крива може бути подана як функцiя абсолютних, так i функцiя вiдносних розстроєк (рис.8.4а):

. (8.4)

Якщо по осi абсцис вiдкладати узагальнену розстройку , отримаємо узагальнену частотну характеристику (8.3), яка поєднує всi варiанти контурiв з будь-якою величиною Q (рис.8.4б). Крива (8.3) не залежить вiд добротностi.

Фазова характеристика контуру також може бути виражена як функцiя вiдносної чи узагальненої розстройки (рис.8.5):

.

а) б)

Рисунок 8.4

а) б)

Рисунок 8.5

8.5 Резонанснi кривi напруг

Резонансна крива напруги  це залежнiсть модуля комплексного дiючого або амплiтудного значення напруги вiд частоти. Для послiдовного резонансного контуру згiдно iз законом Ома виконуються такi спiввiдношення для напруг: ; ; . Пiдставимо сюди значення струму

. Тодi матимемо

; ; .

Модулi здобутих виразiв є резонансними кривими напруг контуру:

; ; .

8.6 Вибiрнiсть резонансного контуру. Смуга пропускання

Вибiрнiсть або селективнiсть  це властивiсть контуру з набору коливань рiзних частот видiляти (пропускати) коливання поблизу резонансної частоти.

Те, наскiльки контур є вибiрним, можна оцiнити за характером резонансних кривих: чим "гострiше" резонансна крива, тим вибiрнішим є контур. Формула (8.4) показує, що чим бiльша добротнiсть Q, тим вища вибiрнiсть.

Частотнi характеристики резонансного контуру за формою значно вiдрiзняються вiд iдеальної П-подібної характеристики. Тому частоти, якi пропускаються контуром, визначають умовно, вводячи поняття смуги пропускання.

Смуга пропускання (П)  це область частот поблизу резонансної частоти, у межах якої струм (напруга) зменшуються не бiльш, нiж у разiв порiвняно з резонансним значенням (рис.8.6а).

Аби визначити смугу пропускання, скористаємось формулою (8.3). За визначенням смуги пропускання . Тобто , звiдки знаходимо два значення узагальненої розстройки, якi вiдповiдають межам смуги пропускання: (рис.8.6б).

Щоб визначити абсолютне значення смуги пропускання (рис.8.6а), скористаємось формулою . Враховуючи, що , знаходимо зв'язок мiж смугою пропускання та добротнiстю:

; .

Для низькодобротних кривих абсолютнi розстройки i . Для високодобротних кривих  .

а) б)

Рисунок 8.6

8.7 Запитання та завдання для самоперевірки

1. Сформулювати умову резонансу в послідовному контурі. Пояснити поняття амплітудного і фазового резонансу.

2. Що таке резонансна частота, характеристичний опір, добротність? За якими формулами вони визначаються?

3. Чому резонанс в послідовному контурі називається резонансом напруг? Зобразити векторну діаграму напруг при резонансі.

4. Зобразити резонансні криві струмів, відкладаючи по осі абсцис частоту, абсолютну і узагальнену розстройки. Як зміниться графік резонансної кривої струму при збільшенні опору у два рази?

5. Пояснити поняття вибірності кола. Дати визначення смуги пропускання.

6. Настроювання контуру на різні частоти здійснюється шляхом зміни ємності контуру. Максимальному значенню пФ відповідає резонансна частота 800 кГц. Яке значення резонансної частоти відповідає мінімуму ємності пФ?

Відповідь: 2 МГц.

7. Обчислити резонансну частоту і частоти, за яких напруги на L і С максимальні у колі з послідовно сполученими R = 50 Ом, L = 10 мГн, С = 1мкФ.

Відповідь: 10 000 Рад/с, 10 700 Рад/с, 9350 Рад/с.

8. У послідовному контурі ЕРС генератора мВ, Ом, мкГн, 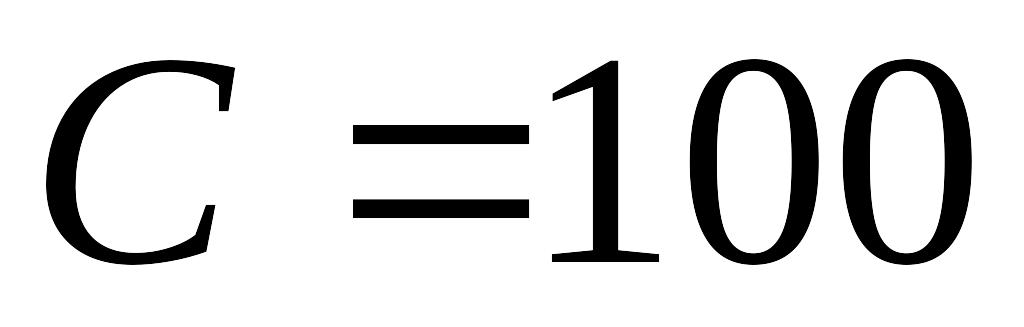пФ. Знайти резонансну частоту, резонансний струм і напругу на елементах контуру, характеристичний опір, добротність, загасання, енергії магнітного і електричного полів.

Відповідь: Рад/с, мА, , Дж.

9. У послідовному контурі ЕРС генератора В, кГц, мА, В. Знайти смугу пропускання контуру. Як зміниться модуль діючого значення струму, якщо, не змінюючи напругу генератора, збільшити його частоту до 812 кГц?

Відповідь: 5,33 кГц; 65 мА.