Лекция 4. Распределение Бернулли, Пуассона, Лапласа Распределение Бернулли

Другие эквивалентные названия этого распределения – биномиальное распределение или задача о повторении однородных независимых испытаний.

Швейцарские математики Иоганн и Якоб Бернулли доказали следующую формулу для расчета Р_n(m) – вероятности числа успехов (m) при n–кратном повторении однородных независимых испытаний, в каждом из которых событие А может появиться с вероятностью р:

.

Д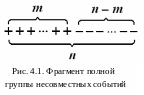 ействительно, представим себе фрагмент полной группы несовместных событий при n–кратном повторении однородных независимых испытаний, где появилось m успехов. Как обычно, появление успеха (события А) будем обозначать знаком "+", а не появление успеха (появление противоположного события ) – знаком "–".

Например, в одном из событий полной группы m успехов были получены в первых m испытаниях (знаки "+" в первых m позициях). Значит, в оставшихся (n – m) испытаниях успехов не было (знаки "–" в оставшихся n – m позициях). Поскольку вероятность успеха р в любом испытании одинакова, то, согласно теореме умножения, вероятность события, изображенного на рис. 4.1, равна произведению вероятностей p^mq^n–m , где q = 1 – p. Порядок появления m успехов (порядок сомножителей р и q) не изменяет произведения вероятноcтей. При повторении однородных независимых испытаний события полной группы с одинаковым числом успехов – равновероятны. Таких равновероятных событий в полной группе будет , т.к. число сочетаний показывает, сколькими способами можно разместить m плюсов (+) на n позициях. Согласно аксиоме сложения, при объдинении несовмесных событий их вероятности складываются, откуда и следует формума Бернулли: .

Можно составить ряд распределения случайной величины X = m – числа успехов в n однородных независимых испытаниях:

X = m	0	1	2	3	…	n
Вер.	Pn(0)	Pn(1)	Pn(2)	Pn(3)	…	Pn(n)

Это распределение зависит от 2-х параметров – р и n .

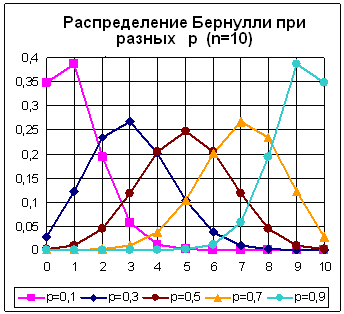
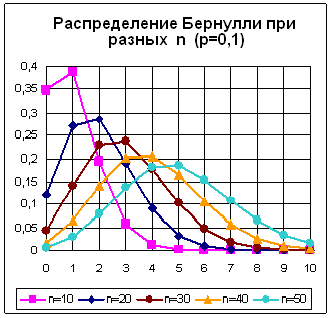
Ниже на рис. 4.2 приведены типичные полигоны распределения Бернулли при различных значениях параметров.

Рис. 4.2. Вид распределения Бернулли при различных значениях параметров

При р = 0,5 распределение симметричное, при р < 0,5 – скошено влево, при р > 0,5 – скошено вправо. При увеличении n  форма распределения приближается к некоторому стандартному симметричному виду (независимо от значения параметра р).

Рассмотрим характеристики распределения Бернулли.

Прежде всего, надо убедиться, что при любых значениях параметров сумма вероятностей Р_n(m) равна единице. Действительно,

.

При суммировании вероятностей Р_n(m) появилась формула бинома Ньютона , поэтому распределение Бернулли называют также биномиальным. Коэффициенты в формуле Бернулли называются еще "биномиальными коэффициентами", они могут быть легко рассчитаны с помощью "треугольника Паскаля":

Биномиальные коэффициенты

(n =1)							1		1
(n =2)						1		2		2
(n =3)					1		3		3		1
(n =4)				1		4		6		4		1
(n =5)			1		5		10		10		5		1
(n =6)		1		6		15		20		15		6		1
(n =7)	1		7		21		35		35		21		7		1

Здесь каждый коэффициент равен сумме двух соседних с ним коэффициентов предыдущего ряда.

Для вычисления математического ожидания и дисперсии требуется суммировать следующие выражения:

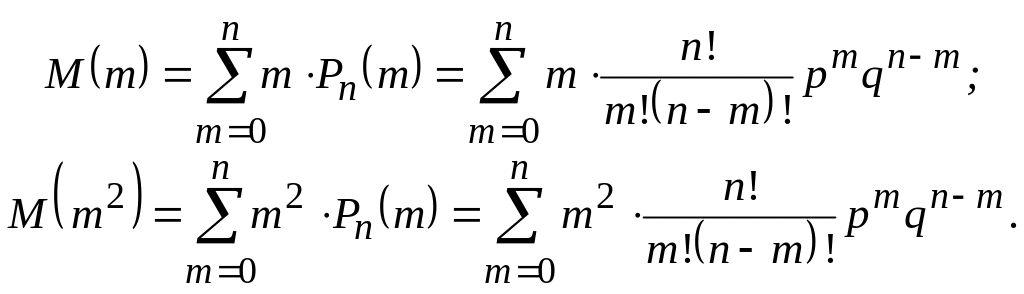
Можно предложить студентам найти способ вычисления сумм M(m), M(m(m–1)), M(m(m–1)(m–2)), но мы вычислим все суммы окольным путем с помощью доказанных ранее свойств математического ожидания и дисперсии.

Напоминаем, что рассматривается задача о повторении однородных независимых испытаний, в каждом из которых случайная величина X_i (число успехов в одном испытании) может принимать только два значения: 0 или 1.

Xi	0	1
Вер.	q	p

Определяем первые три момента распределения для одного испытания: m₁ = 0q + 1p = p, m₂ = 0²q + 1²p = p, m₃ = 0^3q + 1³p = p; откуда M(X_i) = m₁ = p, D(X_i) = m₂ – (m₁)² = p – p² = pq,  ₃(X_i) = m₃ ‑ 3m₁m₂ +2(m₁)³ = pq(q – p).

Общее число успехов при n  испытаний равно сумме X = X₁ + X₂ + … + X_n . Известно, что математическое ожидание суммы случайных величин равно сумме математических ожиданий, дисперсия суммы независимых случайных величин также равна сумме дисперсий, можно показать, что для независимых случайных величин такое же свойство имеет место и для момента 3-го порядка.

Отсюда сразу получаем: M(m) = np, D(m) = npq, ₃(m) = npq(q – p).

.

Можно еще доказать двойное неравенство, однозначно устанавливаю­щее местоположение моды (наивероятнейшего числа успехов при n испытаниях): np – q  Mo  np + p. На интервале длиной (np + p) – (np – q) = = p + q = 1 может быть только одно целое Mo, или же два соседних, если целочисленны края интервала. Предлагается студенту в качестве полезного упражнения самостоятельно вывести это двойное неравенство. Указание: надо в неравенство P_n(Mo–1)  P_n(Mo)  P_n(Mo+1) подставить выражения для P_n(m) и сократить общие множители.

Для примера решим типичную задачу на распределение Бернулли.

Вероятность того, что электротехничный прибор потребует ремонта в гарантийный срок, равна 0,25. Найти вероятность того, что на протяжении гарантийного срока из семи приборов ремонта потребуют m = 0, 1, 2, ... приборов; потребуют ремонта не более четырех, не меньше двух, больше двух и меньше шести приборов.

Решение. Речь идет о повторении однородных независимых испытаний (т.к. p = 0,25 = Const). Число испытаний (число приборов) равно n = 7 (n < 30), поэтому применяем формулу Бернулли.

.

В этой задаче p = 0,25; q = 1 – p = 0,75; биномиальные коэффициенты можно определить также по треугольнику Паскаля.

Для m = 0, 1, 2, ..., 7 расчеты удобно свести в таблицу, в последнем столбце которой приведены накопленные суммы вероятностей (значения кумуляты) F(m). Напоминаем, что функция распределения (кумулята) определена как F(m) = P(X  m), поэтому F(0) = P_n(0) = 0,133484.

m	Cnm	pm	qn–m	Pn(m)	F(m)
0	1	1	0,133484	0,133484	0,133484
1	7	0,25	0,177979	0,311462	0,444946
2	21	0,0625	0,237305	0,311462	0,756409
3	35	0,015625	0,316406	0,173035	0,929443
4	35	0,003906	0,421875	0,057678	0,987122
5	21	0,000977	0,5625	0,011536	0,998657
6	7	0,000244	0,75	0,001282	0,999939
7	1	0,000061	1	0,000061	1,000000

С помощью кумуляты вероятность попадания случайной величины в полуоткрытый интервал m₁ < m  m₂ вычисляется как разность значений функции F(m) на краях этого интервала: P(m₁  m  m₂) = F(m₂) – F(m₁–1). Вычисляем: P(m  4) = F(4) = 0,9871; P(m  2) = P(2  m  7) = F(7) – F(1) = = 1 ‑ 0,4450  = 0,5551; P(2<m<6) = P(3m5) = F(5) – F(2) = 0,9987 ‑ 0,7564 = 0,2422.

Заметим, что во многих учебниках функция F(x) определена немного по-другому: F(x) = P(X < x). Тогда для нашего примера надо было бы принять F(0) = 0 и изменить формулу расчета вероятности попадання случайной величины в полуоткрытый интервал: P(m₁  m < m₂) = F(m₂) – F(m₁) или же P(m₁  m  m₂) = F(m₂+1) – F(m₁). Оба определения функции F(x) эквивалентны, но надо придерживаться одного стандарта.

Вычисляем характеристики распределения Бернулли:

M(m) = np = 70,25 = 1,75; D(m) = npq = 70,250,75 = 1,3125; ; M(m) ‑ q  Mo  M(m) + p; 1,75 – 0,75  Mo  1,75 + 0,25; 1  Mo  2; P(1) = P(2) = P_max .

Согласно правилу "трех сигм" вероятные значения m не превышают M(m) + 3_m = 1,75 + 31,146 = 5,19  5.

Ниже приведен полигон распределения Бернулли для данного примера:

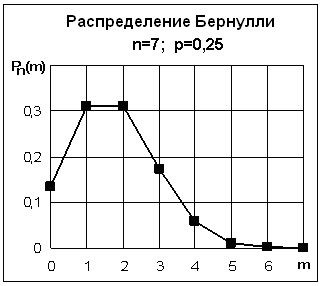
Рис. 4.3. Полигон распределения Бернулли