8.4.2 Деление отрезка в данном отношении
Теорема 8.2. Пусть М1(х1; у1; z1), М2(х2; у2; z2). Если точка М(х0; у0; z0) делит отрезок М1М2 в отношении α, то
,
,
.
(8.3)
Доказательство.
Нетрудно заметить (рисунок 8.14), что
=
+
.
Так как
,
то
=
.
Вектор
=
−
.
Т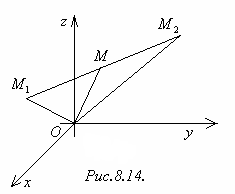
еперь,
=
+ (
−
)
α,
+ α = + α,
(1 + α) = + α,
= (
+
α)
.
П
Рисунок 8.14
,
,
.
Следствие. Пусть М1(х1; у1; z1), М2(х2; у2; z2). Если М0(х0; у0; z0) – середина отрезка М1М2, то
,
,
.
Вопросы для самоконтроля
1. Какая система координат в пространстве называется прямоугольной декартовой?
2. Что называется вектором и как он изображается?
3. Как складываются вектора и что называется их суммой (вектор или скаляр)? Что является проекцией вектора на ось?
4. Что называется координатами вектора?
5. Как находится длина вектора?
6. Как проводится деление отрезка в данном отношении?
9 Скалярное, векторное и смешанное произведения векторов
9.1 Расположение векторов по базисным векторам
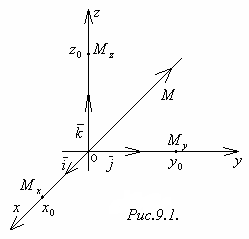
Пусть задана
прямоугольная система координат в
пространстве (рисунок 9.1). Введём в
рассмотрение единичные векторы
координатных
осей Ох, Оу,
Оz,
соответственно. Вектор
одинаково направлен
с осью Оx,
– с осью Оу,
– с осью Оz.
Векторы
называются базисными
векторами системы координат или ортами.
П
Рисунок 9.1
,
,
.
Так как
– диагональ прямоугольного параллелепипеда,
построенного на векторах
,
и
,
то нетрудно заметить, что
=
+
+
,
откуда
=
=
+
+
.
Последняя формула даёт разложение вектора по базисным векторам .
9.2 Скалярное произведение векторов
Определение 9.1. Скалярным произведением двух векторов и называется число, равное произведению их модулей на косинус угла между векторами. Обозначение .
Итак, по определению
=
cosφ,
где φ – угол между
и
.
Свойства скалярного произведения
1.
=
=
cos0
=
.
2. Свойство коммутативности: = .
Действительно,
=
cosφ
=
=
cosφ.
3. Векторы и перпендикулярны тогда и только тогда, когда = 0.
4. Косинус угла φ между векторами и вычисляется по формуле
cosφ
=
.
5. ( α) = ( )α , ( α) ( β) = ( )(αβ).
6. ( + ) = + .
Теорема 9.1. Если векторы = (х1; у1; z1) и = (х2; у2; z2), то
= х1х2 + у1у2 + z1z2.
Доказательство. Запишем разложение векторов и по базисным векторам :
=
+
+
,
=
+
+
.
Тогда, используя свойства скалярного произведения, имеем
= (
+
+
)(
+
+
)
(
)(
)
+ (
)(
)
+ (
)(
)
+
+ (
)(
)
+ (
)(
)
+ (
)(
)
+ (
)(
)
+ (
)(
)
+ (
)(
)
=
(х1х2)
+ (
)у1х2
+ (
)z1x2
+ (
)x1y2
+
(y1y2)
+ (
)z1y2
+ (
)x1z2
+
+ (
)y1z2
+
(z1z2).
Теперь, по свойству
1:
= │
│
= 1,
= 1,
= 1.
По свойству 3:
=
=
=
=
=
= 0.
Следовательно, = х1х2 + у1у2 + z1z2.
Следствие 9.1. Если = (х1; у1; z1) и = (х2; у2; z2), то косинус угла между векторами и вычисляется по формуле
cosφ
=
.
Следствие 9.2. Векторы = (х1; у1; z1) и = (х2; у2; z2) перпендикулярны тогда и только тогда, когда х1х2 + у1у2 + z1z2 = 0.
Пример. Найти угол между векторами = (7; 2; –8) и = (11; –8; –7).
Решение. По следствию 9.1
cosφ
=
.
Тогда φ =
.