2. Оптимізаційні економіко-математичні моделі.

2.1. Загальна постановка задачі лінійного програмування (злп).

Лінійне програмування - напрямок математики, що вивчає ме­тоди рішення екстремальних задач, які характеризуються лінійною залежністю між змінними й лінійним критерієм оптимальності.

До математичних задач лінійного програмування відносять дос­лідження конкретних виробничо-господарських ситуацій, які в тому чи іншому виді інтерпретуються як задачі про оптимальне викорис­тання обмежених ресурсів.

Коло задач, розв'язуваних за допомогою методів лінійного про­грамування досить широке. Це, наприклад:

• задачі про оптимальне використання ресурсів при виробничому пла­нуванні;

• задачі про суміші (планування складу продукції);

• задачі про знаходження оптимальної комбінації різних видів продук­ції для зберігання на складах (керування товарно-матеріаль­ними запасами або "задачі про рюкзак");

• транспортні задачі (аналіз розміщення підприємства, переміщення вантажів).

Економіко-математична модель будь-якої задачі лінійного про­грамування включає: цільову функцію, оптимальне значення якої (ма­ксимум або мінімум) потрібно відшукати; обмеження у вигляді сис­теми лінійних рівнянь або нерівностей; вимогу невід’ємності змінних.

Загальна лінійна економіко-математична модель економічних процесів та явищ — так звана загальна задача лінійного програму­вання подається у вигляді:

1. цільова функція:

F = c₁x₁ + c₂x₂ + ... + c_nx_n → max(min); (2.1)

2. обмеження:

a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n {≤, =, ≥} b₁,

a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n {≤, =, ≥} b₂,

...

a_m1x₁ + a_m2x₂ + ... + a_mnx_n {≤, =, ≥} b_m; (2.2)

3. вимога невід’ємності:

x_j ≥ 0, j = 1,2,…,n... (2.3)

де a_ij, b_i, c_j -задані постійні величини, (i = 1,2,…,m; j=1,2,…,n)

Завдання полягає в знаходженні оптимального значення функції (2.1) при дотриманні обмежень (2.2) і (2.3).

Систему обмежень (2.2) називають функціональними обмежен­нями задачі, а обмеження (2.3) - прямими.

Отже, потрібно знайти значення змінних x₁, x₂, …, x_n, які задово­льняють умови (2.2) і (2.3), і цільова функція (2.1) набуває екстрема­льного (максимального чи мінімального) значення.

Для формалізації задачі лінійного програмування використову­ється поняття n-вимірного векторного простору та поняття скаляр­ного добутку двох векторів у цьому просторі.

Вектором Х=(х₁,х₂,…,х_n) у n-вимірному векторному просторі на­зивається направлений відрізок, який починається на початку коор­динат n-вимірного векторного простору (у точці, усі координати якої дорівнюють нулю) а закінчується у точці з координатами (х₁,х₂,…,х_n).

Введемо поняття скалярного добутку двох векторів. Тут і далі че­рез X,Y позначається скалярний добуток двох векторів-стовпців Х = (х₁, х₂, …, х_n) і Y = (y₁, y₂, …, y_n). За визначенням,

. (2.4)

Визначимо властивості скалярного добутку:

1. Дистрибутивність: x₁+x₂,y=x₁,y+x₂,y;

2. Комутативність: x,y=y,x;

3. Однорідність: x,y=x,y, де  - будь-яке дійсне число;

4. Позитивна визначеність: x,x > 0 для всіх х0.

Дійсний n-вимірний векторний простір, у якому у такий спосіб визначений скалярний добуток називається евклідовим векторним простором Rⁿ.

З урахуванням сказаного задачу лінійного програмування можна подати у компактній векторній формі:

F = CX^T→ max(min) (2.5)

за умов:

АХ {≤, =, ≥} А₀; (2.6)

Х ≥ 0,

де ; ; ; ;

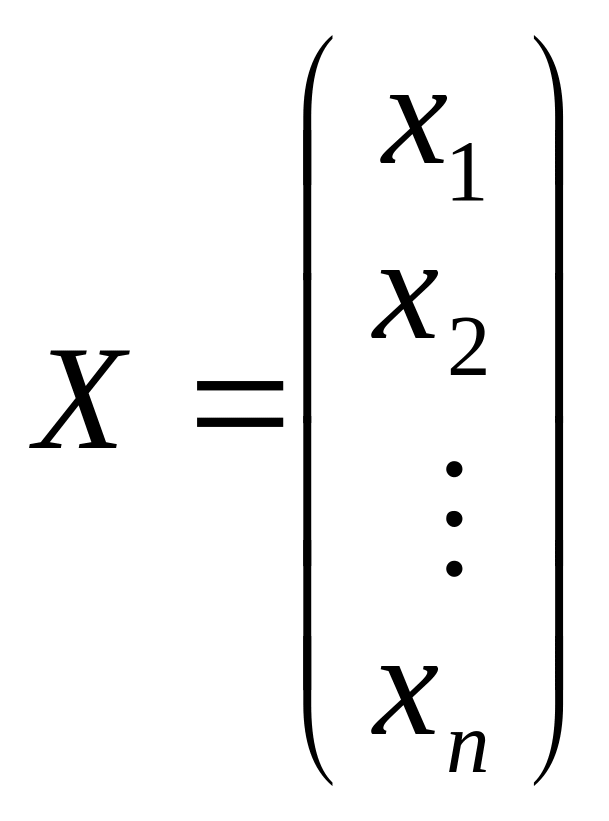X – вектор змінних; С– вектор коефіцієнтів при змінних у цільовій функції; A – матриця коефіцієнтів при змінних у системі обмежень; A₀— вектор вільних членів.

Іноді буває зручним систему функціональних обмежень запису­вати у наступній формі:

A₁x₁ + A₂x₂ + … + A_nx_n {≤, =, ≥} A₀; (2.7)

де

(2.8)

є векторами коефіцієнтів при змінних.

Для загальної задачі лінійного програмування використовуються такі поняття.

Вектор Х = (х₁, х₂, …, х_n), координати якого задовольняють сис­тему обмежень (2.2) та умови невід’ємності змінних (2.3), називається допустимим розв’язком (планом) задачі лінійного програмування.

Якщо множина допустимих розв’язків системи обмежень не є пу­стою (тобто у евклідовому векторному просторі існує хоча б одна, або більше точок, координати яких задовольняють одразу усім обме­женням задачі лінійного програмування), то така система обмежень називається сумісною.

Допустимий план Х=(х₁,х₂,…,х_n) називається опорним планом за­дачі лінійного програмування, якщо він задовольняє не менше, ніж m лінійно незалежних обмежень системи (2.2) у вигляді рівностей, а та­кож обмеження (2.3) щодо невід’ємності змінних.

Опорний план Х=(х₁,х₂,…,х_n), називається невиродженим, якщо він містить точно m додатних змінних, інакше він вироджений.

Опорний план Х^* = (х₁^*,х₂^*,…,х_n^*), за якого цільова функція (2.1) досягає максимального (чи мінімального) значення, називається оп­тимальним розв’язком (планом) задачі лінійного програмування. Оптимальний план є розв’язком задачі лінійного програмування.

Отже, у загальному вигляді задача математичного програмування формулюється так: Знайти такі значення змінних x_j, щоб цільова функція набувала екстремального (максимального чи мінімального значення).