В зависимости от скорости. Критические значения параметров

Используя уравнение энергии

(1.13)

и уравнение состояния для изоэнтропического течения газа

,

выразим параметры течения в произвольном сечении сопла через параметры торможения (p₀, ₀, Т₀) и скорость в этом сечении.

Для определения температуры Т при любой заданной скорости течения воспользуемся уравнением энергии (1.13), переписав его на том основании, что

, в виде ,

где – максимальная теоретическая скорость, которую может достичь поток при его истечении в вакуум. Отсюда

.

Полагая V = 0 и Т = T₀, найдем . Разделив первое из этих двух равенств на второе, получим . Если в этом выражении заменить через по формуле

,

то, сделав замену , получим следующее выражение:

(1.14)

Воспользовавшись формулой , получим аналогичную зависимость для скорости звука:

(1.15)

Чтобы определить давление и плотность, воспользуемся уравнениями изоэнтропического процесса

Сопоставляя эти уравнения с формулой (1.14), находим:

, (1.16)

. (1.17)

Характер изменения относительных параметров газа в зависимости от  виден из графиков рис. 10, построенных по этим формулам для k = 1,405. Как видно, максимальное значение все четыре параметра имеют при скорости, равной нулю: с ростом скорости быстрее всего падает давление, затем плотность, температура и, наконец, скорость звука. По мере приближения к максимальной скорости падение давления и плотности становится замедленным. При достигается полное расширение газа, соответствующее условиям полного вакуума и абсолютного нуля температур (p, , Т и а при этом обращаются в нуль).

Относительные значения параметров газа, представленные формулами (1.14) ... (1.17), можно выразить и через число Маха М. При этом удобнее брать не отношения p/p₀, /₀, ..., а обратные им величины (1.3).

С помощью формул (1.14) ... (1.17) можно найти значения относительных параметров газа в критическом сечении. В этом сечении и  = 1. Подставляя это значение  в указанные формулы, получим:

Для воздуха и всех двухатомных газов (k = 1,405) эти относительные параметры имеют следующие числовые значения:

назад

1.2.4. Скорость истечения и расход газа при истечении из сопла

Рассмотрим истечение газа через сверхзвуковое сопло из достаточно большого резервуара, в котором скорость V₀ может быть принята равной нулю, а давление, плотность и температура равны соответствующим значениям этих параметров при полном торможении.

Определим прежде всего скорость истечения из сопла, т. е. скорость в выходном сечении АА₁ (рис. 9). Напишем уравнение Бернулли для двух сечений, одно из которых взято в резервуаре, второе является выходным сечением:

.

Так как при изоэнтропическом истечении , то формула для расчета скорости истечения принимает вид

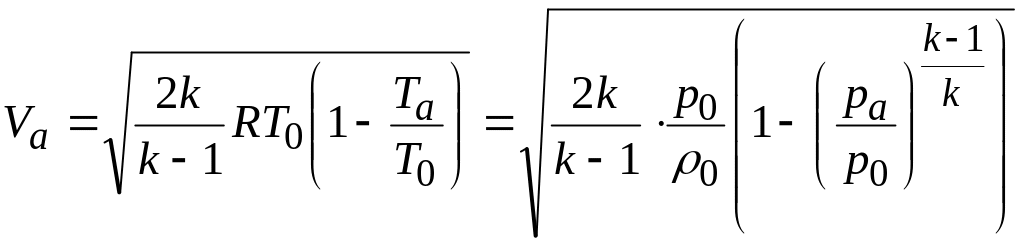. (2.8)

Здесь р_a и Т_a – давление и температура в выходном сечении сопла, равные, соответственно, при дозвуковом истечении внешнему давлению р_н и температуре Т_н окружающей среды.

Из формулы (2.8) видно, что скорость истечения тем больше, чем больше температура в резервуаре Т₀ и чем меньше отношение давления на выходе к давлению торможения. При р_a/p₀ = 1 истечения нет; при р_a/p₀ = 0 скорость истечения равна

.

Расход газа, который во всех сечениях сопла один и тот же, выразим следующим образом:

.

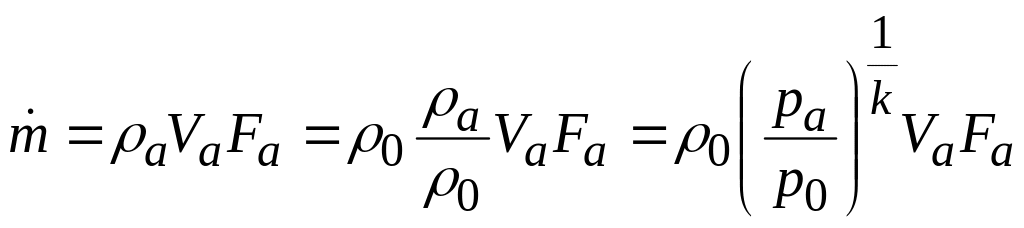Заменяя V_a по формуле (2.8), получим

.

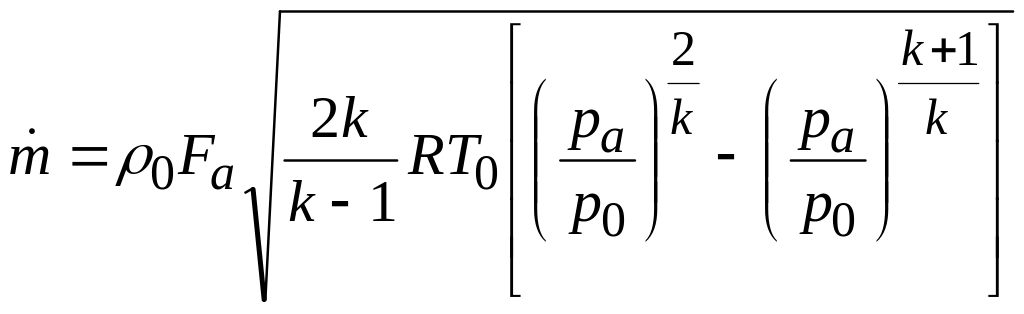С уменьшением относительного давления на выходе р_a/p₀ расход увеличивается, достигая максимума при

.

При дальнейшем уменьшении р_a/p₀ скорость V_a становится сверхзвуковой. В этом случае относительное давление р_a/p₀ перестает влиять на расход.

Действительно, по уравнению постоянства расхода можно написать ,

где – плотность, скорость и площадь сечения в критическом сечении сопла. При сверхзвуковом истечении скорость в этом сечении становится равной критической:

,

т. е. постоянной величине, зависящей только от состояния газа в резервуаре, и остается ею, как бы ни изменялось давление вне сопла. Расход в этом случае будет равен

.

Если принять k = 1.405, R = 287,3 (Дж/кг/К), то имеем

(кг/с).

Рис. 11. Зависимость расхода газа от относительного давления.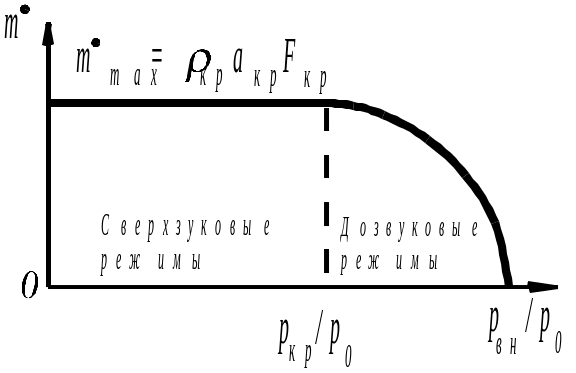

Таким образом, зависит только от состояния газа в резервуаре (р₀, Т₀) и от площади критического сечения сопла . Зависимость расхода от относительного давления р_н /р₀ показана на рис. 11.

Независимость расхода от внешнего давления р_н/р₀ при сверхзвуковом истечении из сопла физически объясняется тем, что изменение внешнего давления р_н распространяется как всякое возмущение со скоростью звука, в то же время скорость V_а на срезе в данном случае больше скорости звука. Поэтому возмущения не в состоянии посредством волны распространяться внутри сопла: они все сносятся потоком наружу. В силу этого обстоятельства давление на выходе р_а только при дозвуковой скорости истечения будет равно внешнему давлению р_н.

При сверхзвуковом истечении р_а должно быть независимо от р_н (хотя, в действительности, в силу нарушения изоэнтропичности истечения р_н оказывает определенное влияние на р_а и при сверхзвуковом истечении), и связано с площадью выходного сечения F_а определенной зависимостью.

1.2.5. Относительная площадь сечения сопла и ее связь назад