
- •1.Правило Крамера для системы 2х линейных уравнений.
- •2.Определители
- •4.Вычисление определителя, приведение к треугольному виду.
- •5.Вычисление определителя методом Лапласа.
- •1.∆≠0 То система (*) имеет 1решение,которое находится по формулам:
- •15Координаты вектора
- •16Декартова прямоугольная система координат.
- •17.Сколярное произведение векторов.
- •18.Векторное произведение векторов.
- •19.Смешенное произведение векторов.
- •21.Общее ур-е прямой, нормальный вектор прямой,взаимное расположение 2х прямых.
- •23.Плоскости
- •24Нормальное ур-е плоскости
- •25.Множества, Понятие функций.
- •26.Абсолютная величина действительного числа
- •27.Основные понятия действительных чисел
- •28.Верхние и нижние границы числовых множеств.
- •29.Понятие функций и гр функций.
- •Предел последовательности
- •31.Символика
- •32.Понятие последовательности и её пределы.
- •34.Бесконечно малые и бесконечно большие послед-ти.
- •35.Монотонные послед-ти
- •Предел и непрерывность функций
- •36.Определение предела функций
- •37.Арифметические операции с пределами функций
- •38.Односторонние пределы
- •39.Бесконечно малые и бесконечно большие величины
- •40.Непрерывность функции
- •41.Односторонняя непрерывность
- •42.Точки разрыва
- •Дифференцирование одного переменного
- •44.Определение производных
- •45.Геометрический смысл производной
- •46.Дифференцирование функций
- •47Дифференциал.
- •48Дифференциалы высших порядков
- •49.Дифференцирование ф-ции заданной параметрически.
- •50.Основные теоремы диф-ого исчисления
- •51.Правило Лапиталя
- •52Формула Тейлора
- •53.Условия монотонности функции
- •54Экстремумы функции
- •55.Выпуклые и вогнутые кривые
- •56.Асимптоты гр функции
17.Сколярное произведение векторов.
Опр1.Сколярным
произведением (а,в)=│а││в│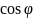 (𝞿⪕Пи)
(𝞿⪕Пи)
Если а=0,в=о,то (а,в)=0
Если (а,в)=0 то а┴в
(а;в)=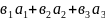
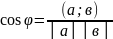 │а│=
│а│=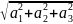
Опр2.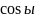 вектора а с осями координат наз
направляющими
вектора а с осями координат наз
направляющими

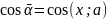
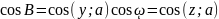
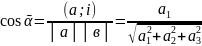
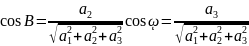
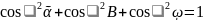
Опр3.Проекцией
АВ на ось наз длина вектора
 ,заключенного
между проекциями начала и конца АВ
причем длина берётся с «+», когда
имеет напр. Отроси и с «-», когда
имеет
противоположное нпр. С ортосью.
,заключенного
между проекциями начала и конца АВ
причем длина берётся с «+», когда
имеет напр. Отроси и с «-», когда
имеет
противоположное нпр. С ортосью.

 В1
А1 А1 В1
В1
А1 А1 В1
е
В А А В
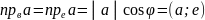 𝞿-⦟
между а и осью в
𝞿-⦟
между а и осью в
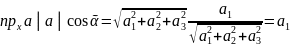
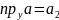
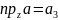
18.Векторное произведение векторов.
│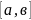 │=│а││в│
│=│а││в│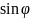 тройка векторов а,в,
правая
тройка векторов а,в,
правая
Векторное произв=0 если хотя бы один из векторов а,в=0
 В
В
С
А аы D
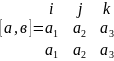
19.Смешенное произведение векторов.
(а,в,с)=(а,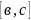 )
=V.если
один из сомножителей=0, то смешенное
произв=0.Если (а,в,с)>0 правая тройка
векторов,(а,в,с)<0левая.
)
=V.если
один из сомножителей=0, то смешенное
произв=0.Если (а,в,с)>0 правая тройка
векторов,(а,в,с)<0левая.
Если а,в,с компланарны то(а,в,с)=0
(а,в,с)=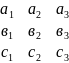
 20.Ур-е
прямой с угловым коэффициентом, ур-е
прямой, проходящей через 2т.,Ур-е прямой
в отрезках.
20.Ур-е
прямой с угловым коэффициентом, ур-е
прямой, проходящей через 2т.,Ур-е прямой
в отрезках.
1.║Ох
у=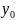
 ║Оу
х=
║Оу
х=
АВ=(х,у-в)
i=(
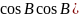 В=
В=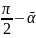 следовательно
следовательно
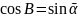
l=(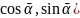 AB║l
AB║l
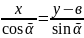 следовательно
у=хtgᾶ-в
у=Кх+в
следовательно
у=хtgᾶ-в
у=Кх+в
2.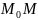 ║l
║l
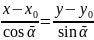
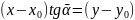
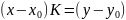 ур-е
пучка прямых
ур-е
пучка прямых
Пр.Зап ур-е прямой ║ прямой у=2х+5 и проходящей через А(-2,3)
К=2 → у-3=2(х+2) у=2х+7
3.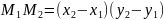
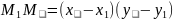
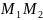 ║
║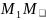
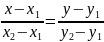
4.АМ=(х-а;у)
АВ=(-а;в)
АВ║АМ
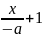 =
=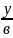
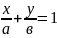
21.Общее ур-е прямой, нормальный вектор прямой,взаимное расположение 2х прямых.
Теор. Общее ур-е прямой
В прямоуг. Декартовых координатах каждая прямая определяется ур-ем 1степени Ах+Ву+С=0 (*)
Ур-е (*) при произвольных А,В,С А,В≠0 одовременно определяют некоторую прямую.
Док-во
Если прямая не ║Оу то у=Кх+в или Кх-у+в=0 А=К В=-1 С=в
Если
прямая ║Оу то х= или х-
=0
А=1 В=0 С=-
или х-
=0
А=1 В=0 С=-
Обратное
утв.
Ах+Ву+С=0 Если В≠0, то у=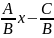
у=Кх+в
К=-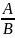 в=-
в=-
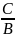 Если В=0, то А≠0 х=-
Если В=0, то А≠0 х=-
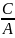 х=
х=
Опр1. Ур-е вида Ах+Ву+С=0 наз общим ур-ем прямой
Теор. N(A,B), координаты которого являются коэф. Перед х,у в общем ур-е прямой Ах+Ву+С=0, ┴ прямой опред. этим ур-ем.
Док-во.
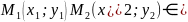 Ах+Ву+С=0
Ах+Ву+С=0
А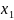 +В
+В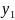 +С=0
_ N(A,B)┴
=
+С=0
_ N(A,B)┴
=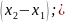 )
)
А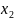 +В
+В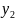 +С=0
+С=0
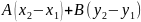 =0
=0
Опр2.
N=(A,B)наз
нормальный вектор прямой Ах+Ву+С=0, а
единичный вектор n=-
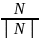 наз
нормаль. Нормальный вектор позволяет
опред. расположение А
+В
+С=0
и А
+В
+С=0
наз
нормаль. Нормальный вектор позволяет
опред. расположение А
+В
+С=0
и А
+В
+С=0
1)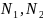 не коллинеарны, то прямые пересекаются
не коллинеарны, то прямые пересекаются
2)
отрогональны(┴),
то прямые
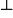
3)
коллинеарны, т.е
 ,
а
,
а
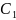 ≠К
≠К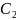 ,
то прямые ║
,
то прямые ║
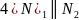 ,
т.е
,
а
=К
,
то прямые совп.
,
т.е
,
а
=К
,
то прямые совп.
Пр.а)через
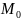 (1;2)
провести прямую ┴2х+3у+5=0
(1;2)
провести прямую ┴2х+3у+5=0
б) через (1;2) провести прямую ║2х+3у+5=0 М(х,у)
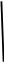 а)
М
║N
а)
М
║N

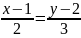


3х-2у+1=0
3х-2у+1=0
б) М ┴N ( М;N) =0 М(х-1;у-2)2(х-1)+3(у-2)=0
2х+3у-8=0
Угол между прямой и плоскостью.
А +В +С=0 и А +В +С 𝞿=?
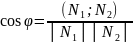 =
=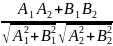 чтоб ⦟=90
чтоб ⦟=90
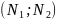 =
=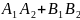 =0
=0
у=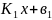 у=
у=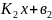
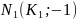
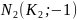
=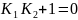
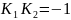 -
условие┴прямых
-
условие┴прямых
22.Нормальное ур-е прямой, расстояние от т. до прямой.
 1)АВ=(х-р
1)АВ=(х-р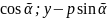 )
)
n=(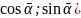 АВ┴n
(AB;n)=0
АВ┴n
(AB;n)=0
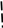
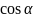 (х-р
(х-р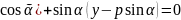
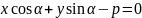 -
нормальное ур-е прямой.
-
нормальное ур-е прямой.
Ах+Ву+С=0
N=(A,B)
n=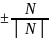 =(
=(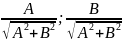 )=(
)=(
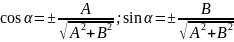
Ах+Ву+С=0
│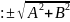
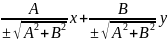
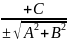 =0(чтоб
перед р был знак -)
=0(чтоб
перед р был знак -)
2)
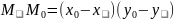
n=(
d=│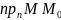 │=│(
│=│(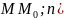 │=│
│=│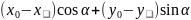 │
│
d=│ │
│
прим.Найти
расстояние от
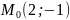 до
прямой 3х-4у+10=0
до
прямой 3х-4у+10=0

 3х-4у+10=0│:(-
3х-4у+10=0│:(-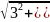 )
)
-3х/5+4у/5-2=0
d=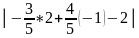 =4
=4
