3. Теоретический материал,

необходимый для выполнения контрольной работы №2.

Задание №1.

• Уравнение прямой, проходящей через две точки:

• Пусть прямые заданы каноническими уравнениями

и

Если прямые параллельны, то параллельны их направляющие вектора и , т.е.

Если прямые перпендикулярны, то перпендикулярны их направляющие вектора и , т.е.

• Расстояние от точки М(X, Y, Z) до прямой

определяется по формуле

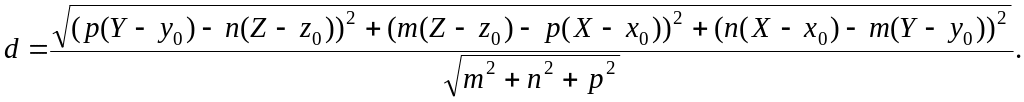
• Уравнение плоскости, проходящей через точку М₀(x₀,y₀,z₀) и имеющей нормальный вектор :

• Уравнение вида

называется общим уравнением плоскости.

• Уравнение плоскости, проходящей через три точки:

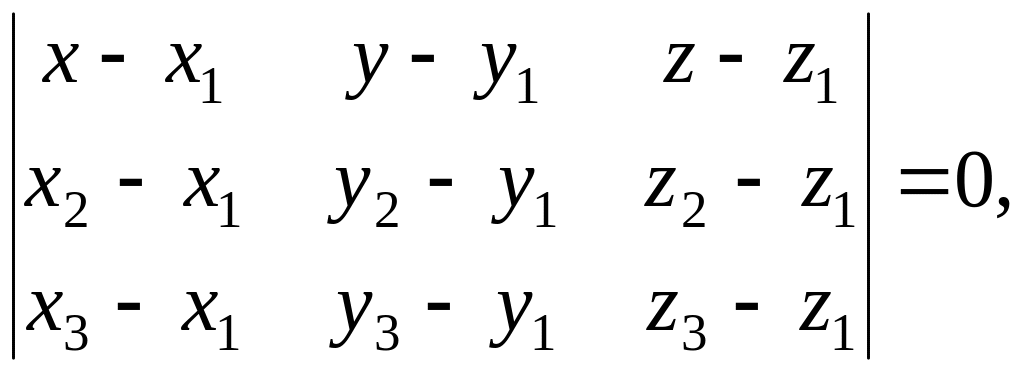
где М₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂), M₃(x₃,y₃,z₃) − точки, не лежащие на одной прямой.

• Расстояние от точки М₀(x₀,y₀,z₀) до плоскости :

• Угол, образованный двумя плоскостями и :

Условие параллельности:

Условие перпендикулярности:

• Угол между прямой и плоскостью :

Условие параллельности:

Условие перпендикулярности:

Задание 2.

Рассмотрим задание 2, где предлагается привести к каноническому виду уравнение поверхности второго порядка с помощью теории квадратичных форм.

Рассмотрим общее уравнение поверхности второго порядка

a₁₁x²+2a₁₂xy+2a₁₃xz+a₂₂y²+2a₂₃yz+a₃₃z²+2b₁x+2b₂y+2b₃z+c=0,

которое только при специально выбранной системе координат является каноническим (простейшим) уравнением.

Выпишем отдельно слагаемые второго порядка относительно координат х, у, z. Они образуют так называемую квадратичную форму Φ(х,у,z), которую можно записать так:

Φ(х,у,z) = a₁₁x²+a₁₂xy+a₁₃xz+

+a₂₁yx+ a₂₂y²+ a₂₃yz+

+a₃₁zx+a₃₂zy+ a₃₃z²,

где а_ij=a_ji, i, j =1,2,3.

Матрица этой квадратичной формы:

.

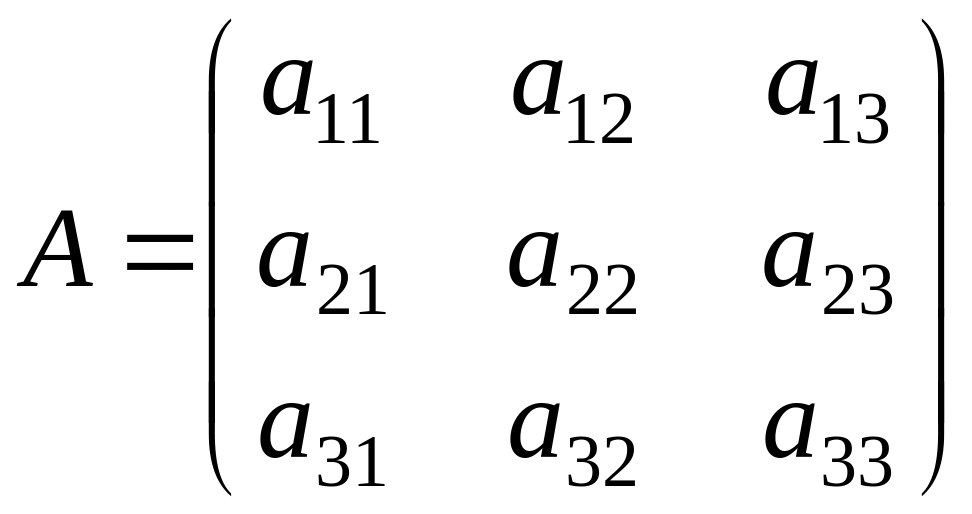Нетрудно заметить, что она симметрическая, т.е. является матрицей самосопряженного оператора А. Если ввести в рассмотрение матрицу-столбец

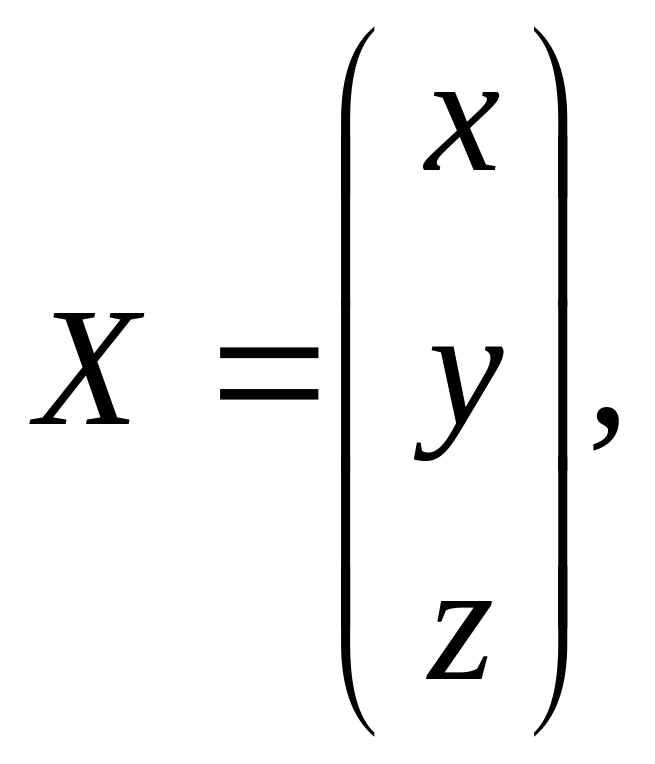
то квадратичную форму Φ(х,у,z) в матричном виде можно записать так:

Φ(х,у,z) = Х^Т∙А∙Х.

С помощью ортогонального преобразования Х = Т∙Х^', которому с геометрической

точки зрения в общем случае соответствует поворот координатных осей и, может быть, изменение их направления, приведем квадратичную форму к простейшему виду

Φ^'(х^',у^',z^') = (Х^')^Т∙А^'∙Х^'.

Матрица А^' имеет диагональный вид, по главной диагонали ее стоят собственные числа матрицы А: λ₁, λ₂, λ₃. В координатной форме канонический вид квадратичной формы записывается так:

Φ^'(х^',у^',z^') = λ₁х'²+ λ₂у'²+ λ₃z'².

Столбцы ортогональной матрицы преобразования Т формируются из координат единичных собственных векторов матрицы А: Λ^е₁, Λ^е₂, Λ^е₃.

Таким образом, задача свелась к нахождению собственных чисел λ₁, λ₂, λ₃ и соответствующих им единичных собственных векторов матрицы А. Для нахождения собственного вектора Λ=(α, β, γ)^Т имеем уравнение А∙Λ=λ∙Λ или (А−λ∙Е)∙Λ=0. В координатной форме оно имеет вид

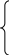(а₁₁−λ)α+а₁₂β+а₁₃γ=0,

а₂₁α+(а₂₂−λ)β+а₂₃γ=0, (*)

а₃₁α+а₃₂β+(а₃₃−λ)γ=0.

Решив характеристическое уравнение

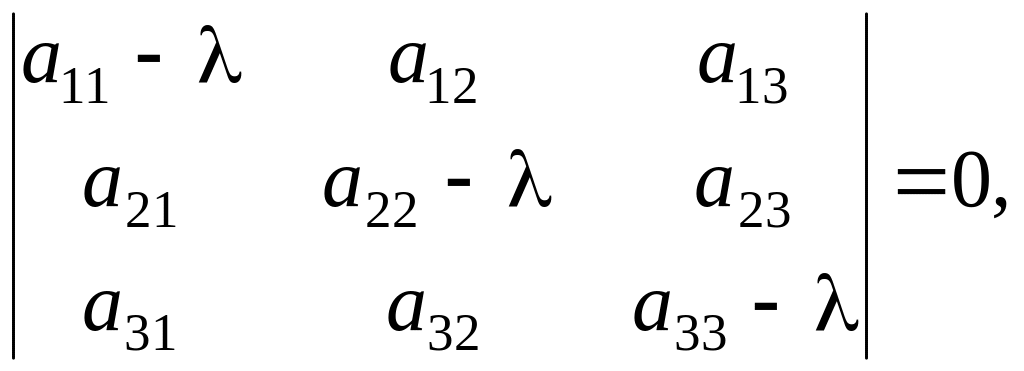
найдя его корни λ₁, λ₂, λ₃ и подставляя по очереди λ= λ₁, λ= λ₂, λ= λ₃ в систему (*), найдем три ненулевых решения этой системы, т.е. три собственных вектора:

, , .

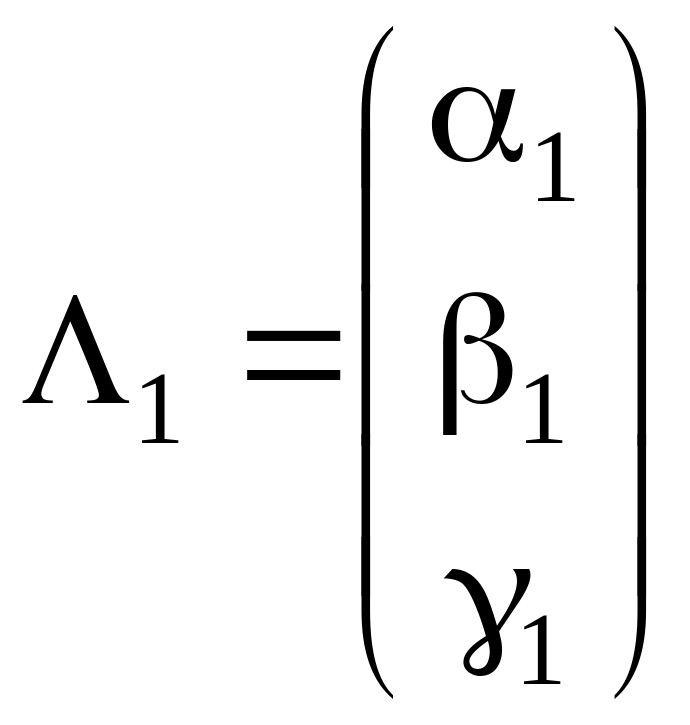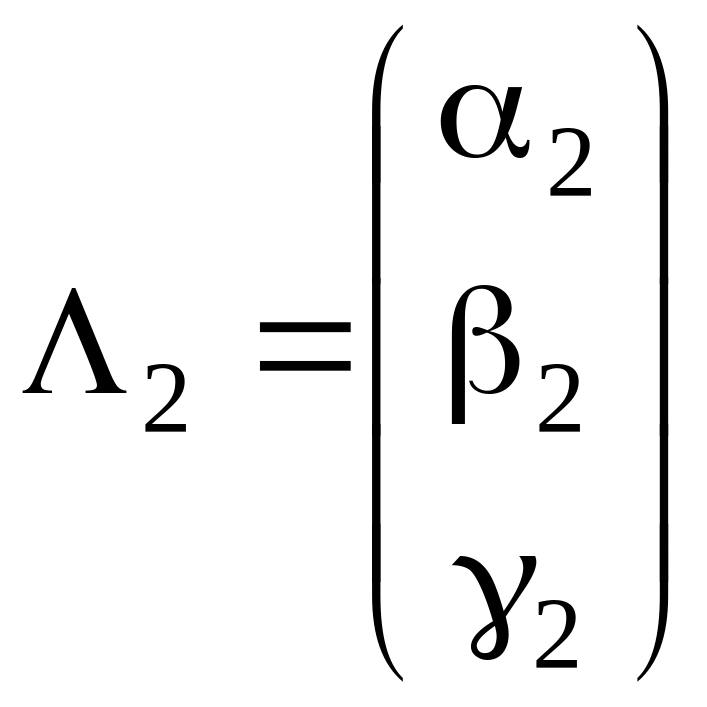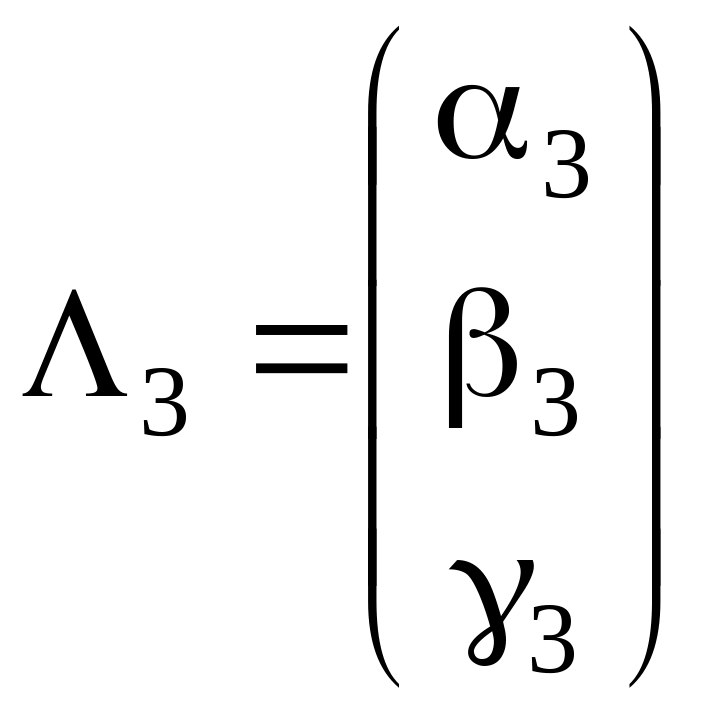Пронормировав их, т.е. разделив координаты каждого вектора на его длину

найдем три единичных собственных вектора Λ^е₁, Λ^е₂, Λ^е₃. Записав координаты этих векторов в качестве столбцов, построим матрицу преобразования координат Т. Заметим, что преобразованию с матрицей Т будет соответствовать правая система координат, если detT = 1, что нетрудно добиться переставляя векторы Λ^е₁, Λ^е₂, Λ^е₃.

В координатной форме преобразование Х = Т∙Х^' запишется так:

х = t₁₁x^'+t₁₂y^'+t₁₃z^',

y = t₂₁x^'+t₂₂y^'+t₂₃z^',

z = t₃₁x^'+t₃₂y^'+t₃₃z^'.

В результате уравнение поверхности второго порядка приняло вид:

λ₁х'²+ λ₂у'²+ λ₃z'²+2b'₁ x^'+2b'₂ y^'+2b'₃ z^'+c^'=0.

Осуществив преобразование параллельного переноса по формулам

х' = х₀ + х'',

у^' = у₀ + у'',

z^' = z₀ + z^'',

приведем уравнение поверхности к каноническому виду. По каноническому виду нетрудно определить тип поверхности и сделать ее схематический рисунок.

Пример. Привести к каноническому виду уравнение поверхности второго порядка х²+4ху+у²+2z²−6=0 с помощью теории квадратичных форм. Найти матрицу преобразования и выписать формулы преобразования координат. Указать тип поверхности.

Решение. Напишем уравнение этой поверхности в общем виде, выписывая и коэффициенты, равные нулю:

1∙x²+2∙xy+0∙xz+

+2∙yx+1∙y²+0∙yz+

+0∙zx+0∙zy+2∙z²−6=0.

Теперь нетрудно записать и матрицу этой квадратичной формы:

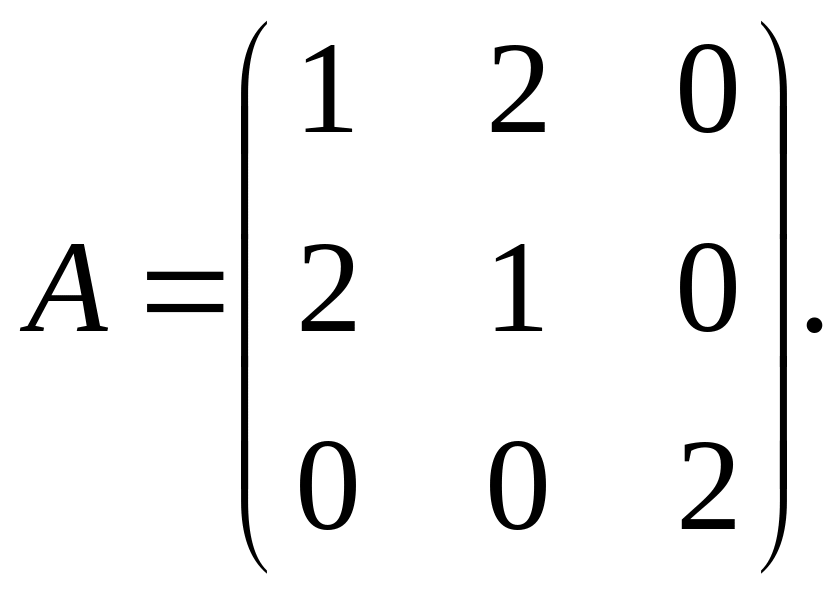
Характеристическое уравнение имеет вид

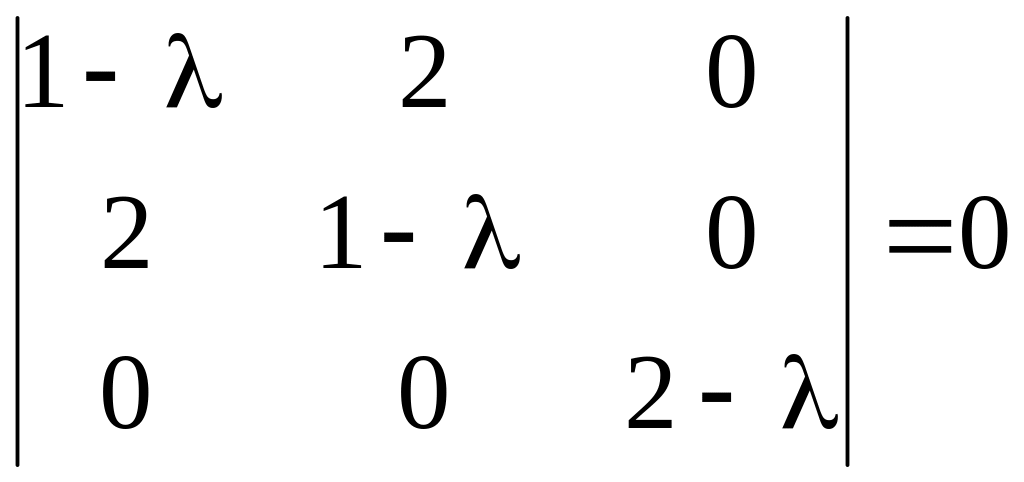
или (λ−3)(λ−2)(λ+1)=0. Его корни, очевидно, λ= 3, λ= 2, λ= ­­­­­­−1.

Найдем соответствующие им единичные собственные векторы Λ^е₁, Λ^е₂, Λ^е₃. Решаем систему

(1−λ)α+2β=0,

2α+(1−λ)β=0,

(2−λ)γ=0.

Подставляем по очереди λ=λ₁=3, λ=λ₂=2, λ=λ₃=−1. При λ=3 имеем

−2α₁+2β₁=0,

2α₁−2β₁=0,

−γ₁=0.

Очевидно, второе уравнение является следствием первого, т.е. фактически имеем систему двух уравнений с тремя неизвестными:

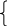−2α₁+2β₁=0,

−γ₁=0.

Она имеет бесчисленное множество решений. Найдем одно ненулевое. Полагая β₁=1, получаем α₁=1. Очевидно, γ₁=0. Итак,

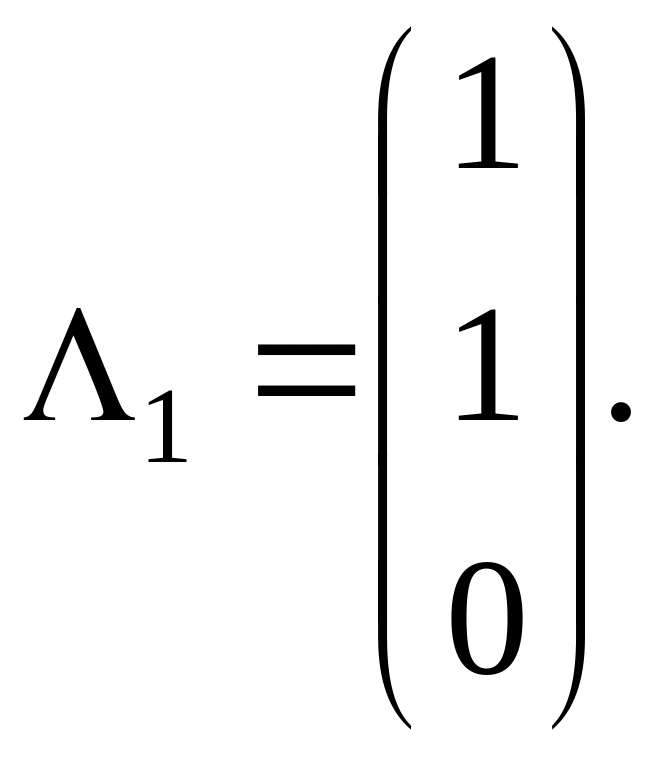
При λ=2 имеем

−α₂+2β₂=0,

2α₂−β₂=0,

0∙γ₂=0.

Очевидно, α₂=β₂=0, γ₂ − любое ненулевое. Полагаем γ₂=1. Итак,

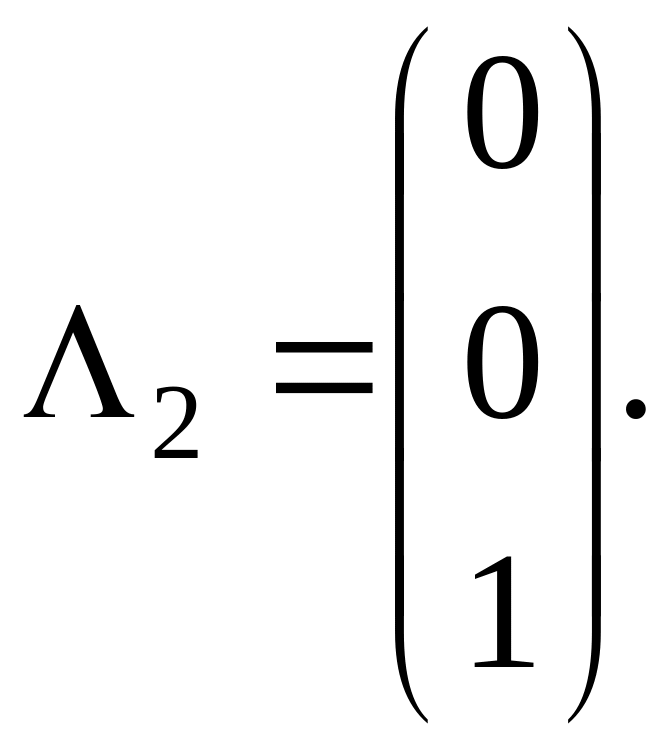
При λ=−1 имеем

2α₃+2β₃=0,

2α₃+2β₃=0,

3γ₃=0

или α₃+β₃=0, γ₃=0. Полагая β₃=−1, получаем α₃=1. Очевидно, γ₃=0. Итак,

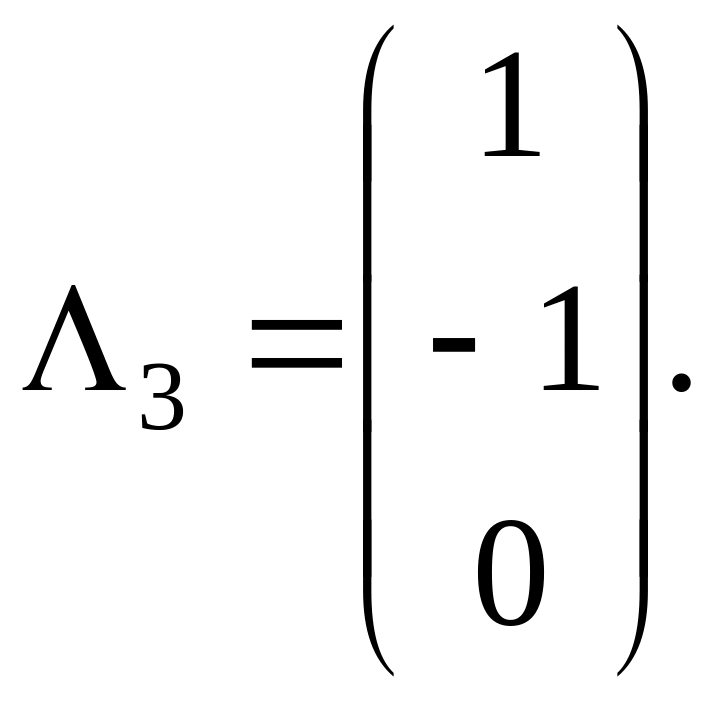
Нормируем собственные векторы. , , , откуда

Λ^е₁=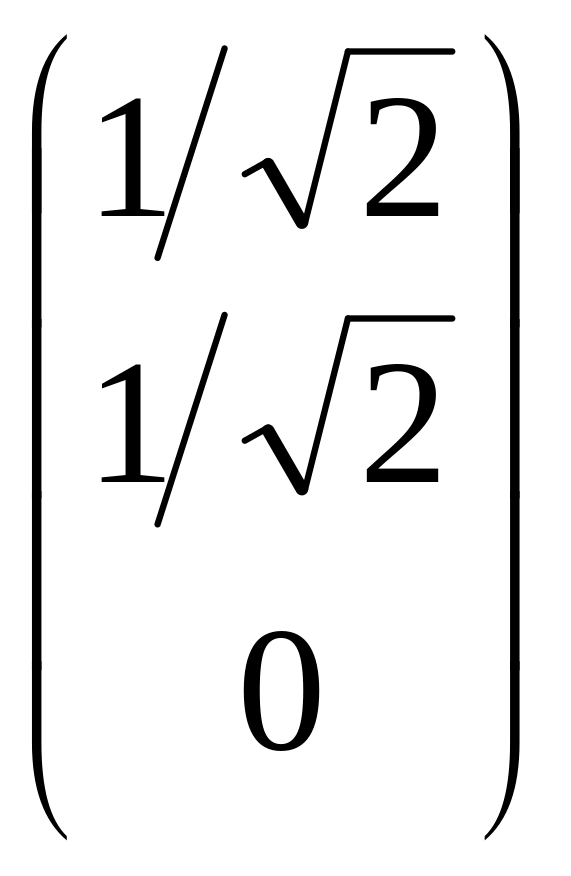 , Λ^е₂= , Λ^е₃= .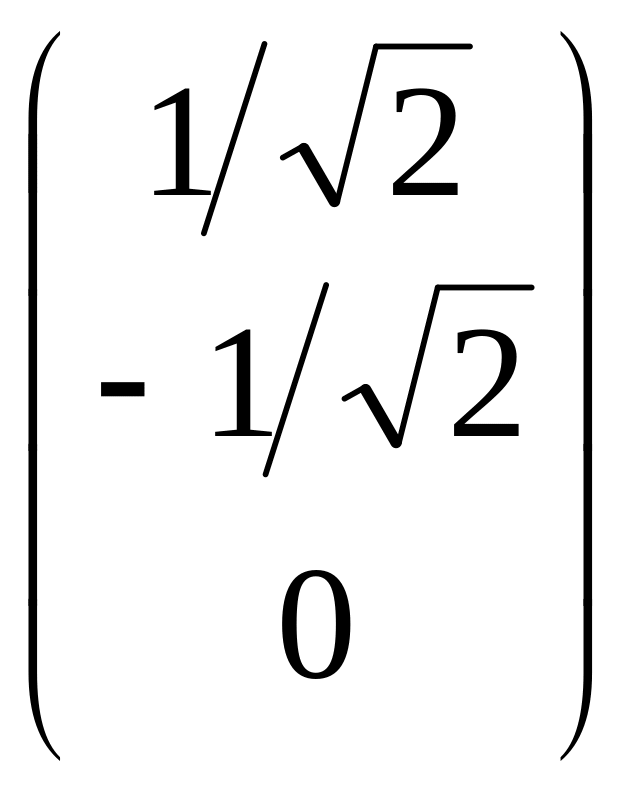

Формируем матрицу преобразования Т, беря в качестве ее столбцов собственные векторы Λ^е₁, Λ^е₂, Λ^е₃.

Получаем

Т=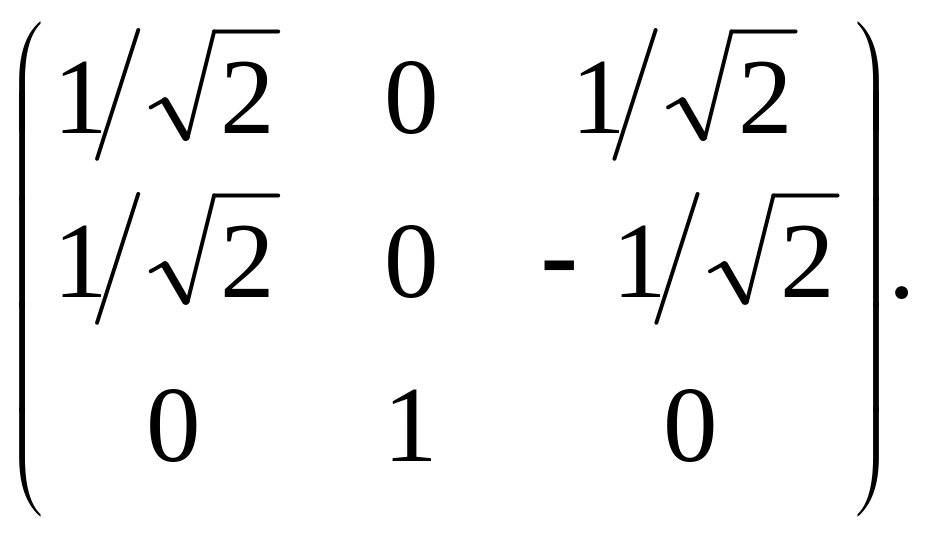

Очевидно, detT = 1, т.е, система координат Ох^'у^'z^' будет правой.

Итак, имеем преобразование Х = Т∙Х^'. В координатной форме

или

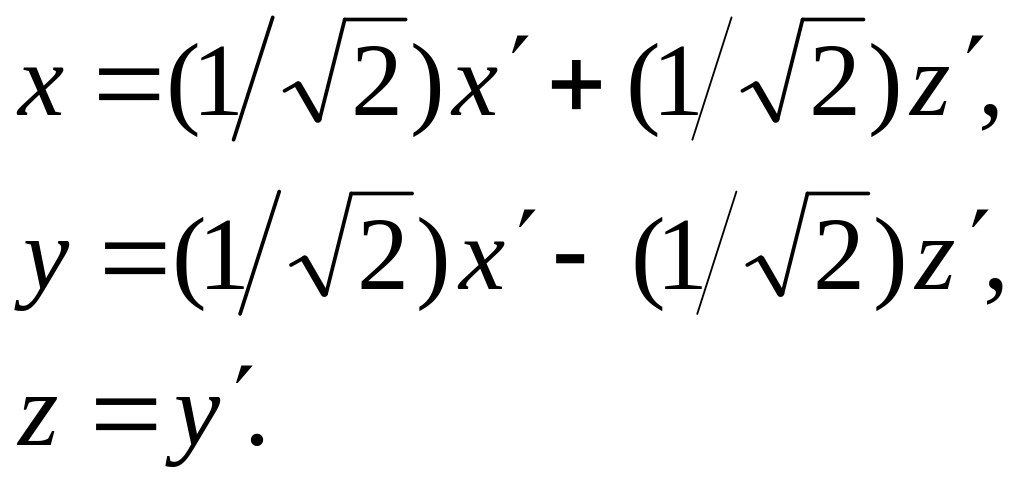
Уравнение поверхности в системе координат Ох^'у^'z^'

3х'²+ 2у'²−z'²−6=0

или

Это уравнение определяет однополостный гиперболоид.

Замечание. Кроме цилиндрических, существует шесть основных видов поверхностей второго порядка, определяемых следующими каноническими уравнениями:

• эллипсоид

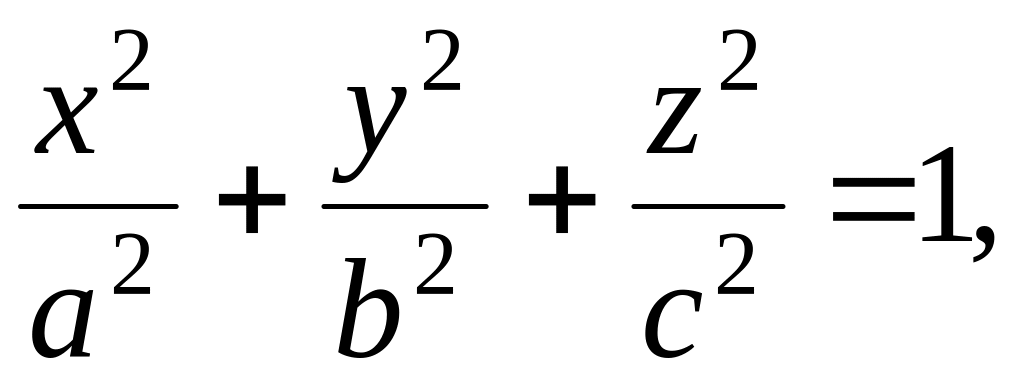
• однополостный гиперболоид

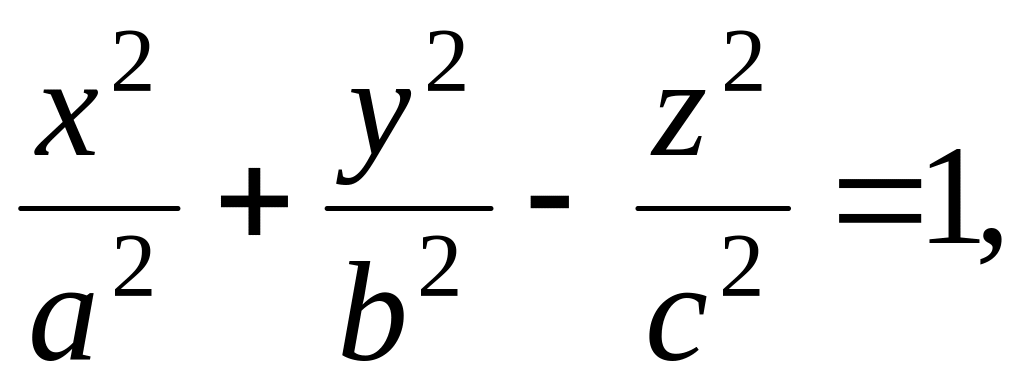
• двуполостный гиперболоид

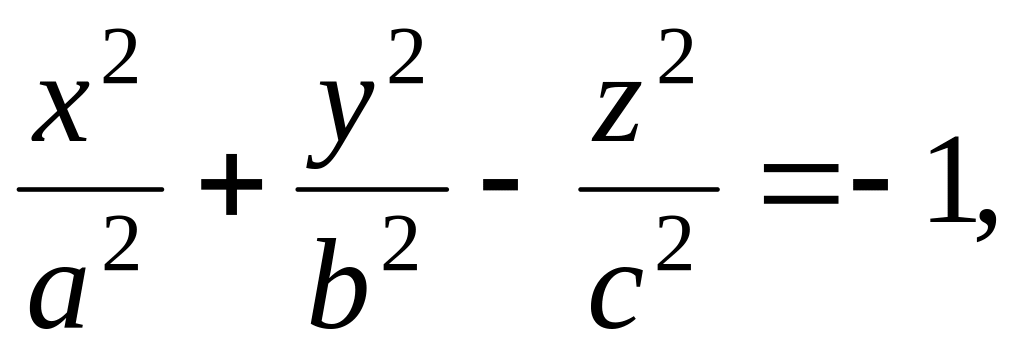
• конус второго порядка

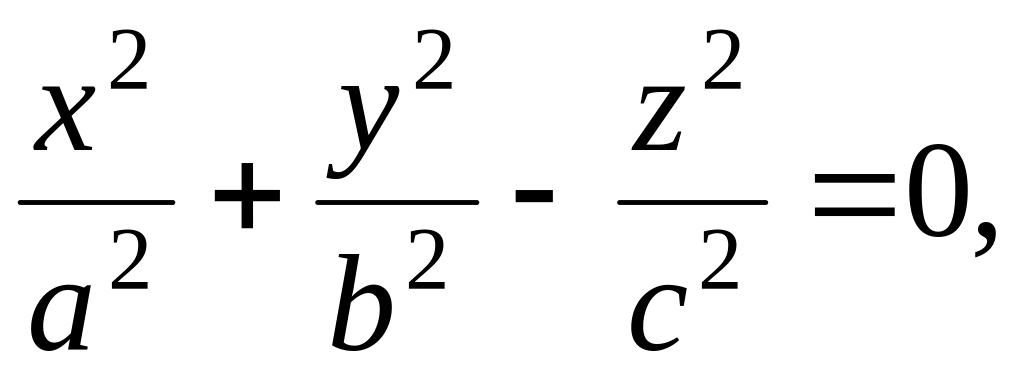
• эллиптический параболоид (pq > 0)

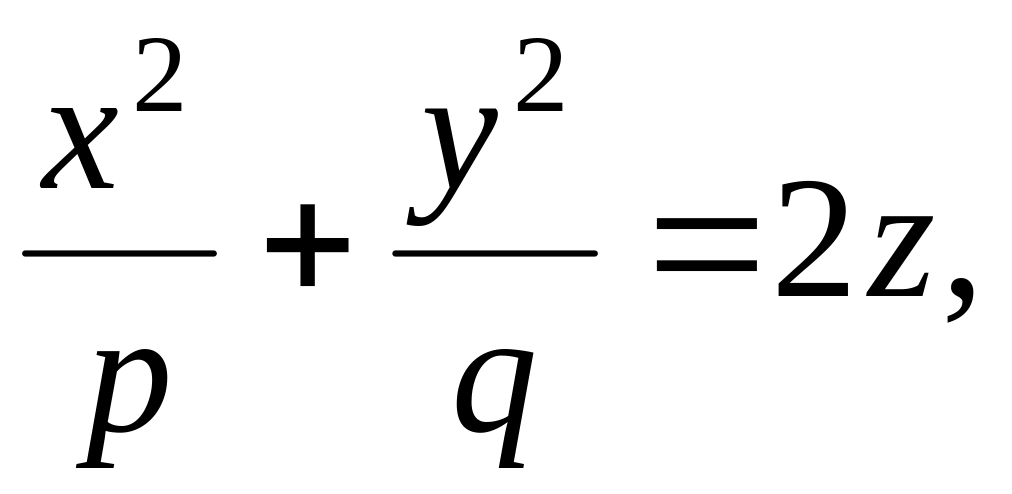
• гиперболический параболоид (pq > 0)