18

Министерство образования Российской Федерации

Брянский государственный технический университет

“УТВЕРЖДАЮ”

Ректор университета

___________А.В. Лагерев

“____”___________2004 г.

МАТЕМАТИКА

АЛГЕБРА И ГЕОМЕТРИЯ

Методические указания и контрольные задания

для студентов специальности “Программное обеспечение

вычислительной техники и автоматизированных

систем” заочной формы обучения (2 семестр)

Брянск 2004

УДК 516.1/4

Математика. Алгебра и геометрия. Методические указания и контрольные задания для студентов специальности “Программное обеспечение вычислительной техники и автоматизированных систем” заочной формы обучения (2 семестр). − Брянск: БГТУ, 2004 − 19 с.

Алексей Петрович Мысютин

канд. техн. наук, доцент

Рекомендовано кафедрой “Высшая математика” БГТУ

(протокол №5 от 19.01.2004 г.)

Научный редактор Ольшевская Н.А.

Редактор Королева Т.И.

Компьютерный набор Левкина А.П.

Темплан 2004 г., п.19

Подписано в печать 02.02.2004 Формат 60х84 1/16 Бумага офсетная

Офсетная печать. Печ. л. 1,19 Уч.-изд. л. 1,19 Т. 30 экз. Заказ

Издательство Брянского государственного технического университета

Брянск, бульвар 50-летия Октября, 7

Лаборатория оперативной печати БГТУ, ул. Институтская, 16.

Студенты первого курса заочной формы обучения специальности “Программное обеспечение вычислительной техники и автоматизированных систем” во втором семестре должны выполнить две контрольные работы. Обе контрольные работы посвящены изучению аналитической геометрии. В первой работе представлены задания только по аналитической геометрии на плоскости, а во второй − по аналитической геометрии в пространстве.

Для выполнения первой работы требуется знание таких разделов теории как прямая на плоскости, канонические уравнения линий второго порядка, преобразование систем координат на плоскости, приведение общего уравнения линии второго порядка к каноническому виду, полярная система координат и построение графиков функций в этой системе.

Вторая контрольная работа состоит всего из двух задач, но первую задачу можно рассматривать как комплексное расчетное задание по темам прямая линия в пространстве, плоскость, взаимное расположение прямых и плоскостей в пространстве. Во второй задаче предлагается привести к каноническому виду уравнение поверхности второго порядка с помощью теории квадратичных форм.

В параграфах 1 и 3 приведены формулы, определения и другие краткие пояснения теории, необходимые для решения задач контрольных работ. Сложные задачи (№3 из контрольной работы №1 и №2 из контрольной работы №2) рассмотрены подробно как в теоретическом, так и в практическом аспекте. В пособии подробно разобраны три примера решения типовых задач.

Более полную информацию по изучаемым во втором семестре разделам курса алгебры и геометрии можно получить в следующих учебных пособиях:

1. Ефимов Н.Е. Краткий курс аналитической геометрии. (Любое издание, начиная с десятого).

2. Привалов И.И. Аналитическая геометрия. (Любое издание, начиная с шестого).

3. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. (Любое издание, начиная со второго).

4. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. − 2-е изд., испр. − М.: Айрис-пресс, 2002. − 288 с.: ил.

5. Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах. Ч. I: Учеб. пособие для студентов втузов. (Любое издание, начиная с третьего).

6. Выгодский М.Я. Справочник по высшей математике. (Любое издание, начиная с шестого).

1.Теоретический материал, необходимый для выполнения

контрольной работы №1.

Задание 1.

• Уравнение прямой линии, проходящей через заданную точку в заданном направлении:

y = y₀ +k(x  x₀).

Здесь k  тангенс угла, образованного прямой с положительным направлением оси Ох (угловой коэффициент), (х₀,у₀)  координаты точки, через которую проходит прямая.

• Уравнение прямой линии, проходящей через две данные точки а(х1,у1) и в(х2,у2):

• Расстояние d от точки (х₀,у₀) до прямой Ах+Ву+С=0:

• Условие параллельности для прямых у=k₁x+b₁ и у=k₂x+b₂: k₁ = k₂.

• Условие параллельности для прямых А₁х+В₁у+С₁=0 и А₂х+В₂у+С₂=0:

• Условие перпендикулярности для прямых у=k₁x+b₁ и у=k₂x+b₂: k₁ k₂=1.

• Условие перпендикулярности для прямых А₁х+В₁у+С₁=0 и А₂х+В₂у+С₂=0:

• Деление отрезка пополам. Координаты середины отрезка А₁А₂ равны полусуммам соответственных координат его концов:

Задание 2.

• Окружность. Уравнение окружности с центром в точке С(a;b) и радиусом, равным R:

• Эллипс. Каноническое уравнение

Координаты фокусов: (-с;0) и (с;0), где с=

Эксцентриситет:

Уравнения директрис:

• Гипербола. Каноническое уравнение

Координаты фокусов: (-с;0) и (с;0), где с=

Уравнения асимптот:

Эксцентриситет:

Уравнения директрис:

• Парабола. Каноническое уравнение

Координаты фокуса: ( ,0).

Уравнение директрисы:

Задание 3.

Переход от одной системы координат в какую-либо другую называется преобразованием системы координат.

Координаты (х; у) в данной системе преобразуются к координатам (Х, Y) в новой системе по формулам:

при параллельном сдвиге осей и переносе начала координат в точку О₁(х₀, у₀)

х=x₀+X, y=y₀+Y;

при повороте осей на угол 

x=XcosYsin, y=Xsin+ Ycos.

Рассмотрим теперь общее уравнение второй степени относительно х и у:

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0. (1)

Допустим, что B≠0. В этом случае преобразование уравнения (1) к простейшему виду осуществляется путем поворота и параллельного переноса координатных осей.

Используя формулы поворота осей

x=XcosYsin, y=Xsin+ Ycos,

выразим старые координаты через новые:

А(XcosYsin)²+2B(XcosYsin)( Xsin+ Ycos)+C(Xsin+ Ycos)²+

+2D(XcosYsin)+2E(Xsin+ Ycos)+F=0

или

(A∙cos²α+2Bsincos+Csin²)∙X²+2((C−A)sincos+B(cos²− sin²))∙X∙Y+ +(A∙sin²α−2Bsincos+Ccos²)∙Y²+

+2(Dcos+Esin)∙X+2(−Dsin+Ecos)+ F=0.

Выберем угол α так, чтобы коэффициент при X∙Y обратился в нуль, т.е. чтобы

выполнялось равенство

2(C−A)sincos+2B(cos²− sin²)=0

т.е.

B∙tg²α−(C−A) ∙tgα−B=0.

Отсюда

tgα = (2)

Заметим, что эти значения tgα соответствуют двум взаимно перпендикулярным направлениям. Поэтому, взяв

tgα =

вместо

tgα =

мы только меняем ролями оси X и Y.

Получив tgα, воспользуемся известными из тригонометрии формулами

и

для определения новых коэффициентов

А₁= A∙cos²α+2Bsincos+Csin²,

С₁= A∙sin²α−2Bsincos+Ccos²,

D₁= Dcos+Esin

и

Е₁=−Dsin+Ecos.

В результате преобразованное уравнение линии примет вид:

A₁X²+C₁Y²+2D₁X+2E₁Y+F=0, (3)

где все коэффициенты известны.

Если в уравнении вида (3) линии второго порядка А₁∙С₁>0, то говорят, что это уравнение определяет линию эллиптического типа; если же А₁∙С₁<0, то говорят, что уравнение определяет линию гиперболического типа и, наконец, если один из коэффициентов А₁ или С₁ равен нулю, т.е. А₁∙С₁=0, то уравнение определяет линию параболического типа.

Далее надо рассмотреть два случая: 1) А₁∙С₁ ≠ 0; 2) А₁∙С₁ = 0.

Случай 1. Сделаем параллельный перенос по формулам X=x₀+x', Y=y₀+y'. Получим

A₁(x₀+x')²+C₁(y₀+y')²+2D₁(x₀+x')+2E₁(y₀+y')+F=0

или

A₁x'²+C₁y'²+2(A₁x₀+D₁)x'+2(C₁y₀+E₁)y'+(A₁x₀²+C₁y₀²+2D₁x₀+2E₁y₀+F)=0.

Приравняв к нулю коэффициенты при x' и y', получим

Точка O'(x₀, y₀) является началом новой системы координат O'x'y'. Уравнение кривой в этой системе

A₁x'²+C₁y'²+F₁=0.

Случай 2. Пусть С₁=0 (для случая А₁=0 вычисления те же, только x' и y' меняются местами). Уравнение кривой имеет вид

A₁X²+2D₁X+2E₁Y+F=0. (4)

Если Е₁ ≠ 0, то уравнение (4) можно разрешить относительно Y:

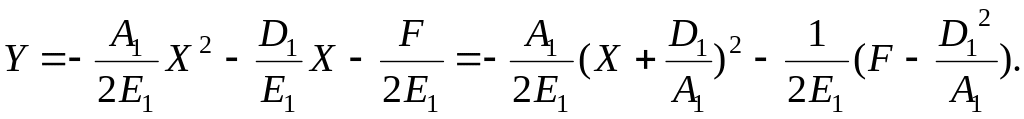
Имеем параболу. Сделаем параллельный перенос по формулам X=x₀+x', Y=y₀+y',

где

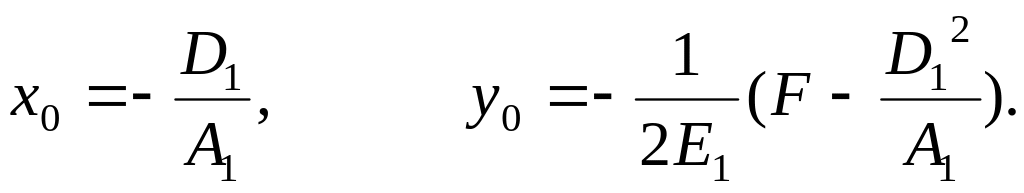
Точка O'(x₀, y₀) является началом новой системы координат O'x'y'. Уравнение кривой в этой системе

При Е₁ = 0 уравнение (3) представляет при D₁²−A₁F₁>0 пару параллельных прямых, при D₁²−A₁F₁<0 − пару мнимых параллельных прямых, при D₁²−A₁F₁=0 − две слипшиеся прямые.

Пример 1. Преобразовать к каноническому виду уравнение и построить кривую

3х²−4ху+3у²+4х+4у−1=0.

Решение. По условию задачи А=3, В=−2, С=3, D=2, Е=2, F=−1. По формуле (2) имеем tgα=±1. Возьмем α=π/4. После вычисления коэффициентов получим

X²+5Y²+4√2∙X–1=0.

Сделаем теперь параллельный перенос по формулам X=x₀+x', Y=y₀+y'. Уравнение примет вид:

x'²+5y'²+(2x₀+4√2)x'+10y₀y'+(x₀²+5y₀²+4√2∙x₀−1)=0.

Приравняв к нулю коэффициенты при x' и y', получим x₀=−2√2, y₀=0. Точка O'(−2√2, 0) является началом новой системы координат O'x'y'. Уравнение кривой в этой системе имеет вид

x'²+5y'²−9=0

или

Это − эллипс с полуосями а=3 и b=3/√5.

Сделаем рисунок. Строим систему координат Оху. Находим в этой системе координаты точки О' по формулам поворота осей

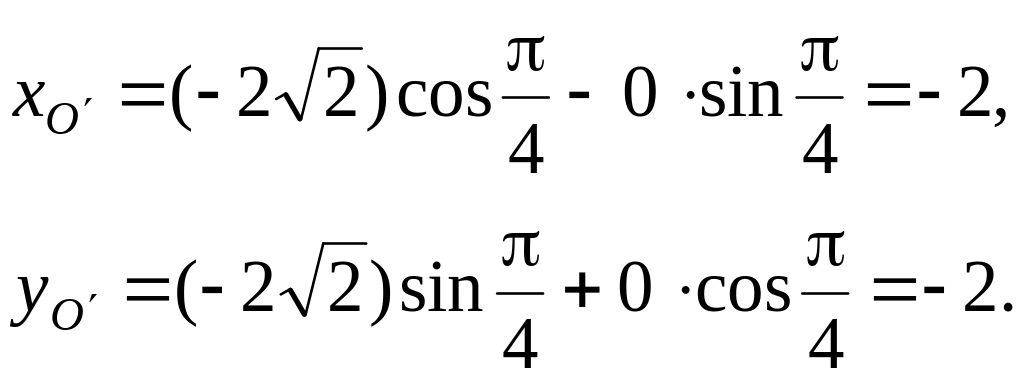
Проводим через точку О' ось х' новой (канонической) системы координат под углом α=π/4 к оси Ох. Направление оси О'у' находим путем поворота оси О'х' на угол 90^о против хода часовой стрелки.

Определяем координаты точек пересечения (если они есть) эллипса с координатными осями исходной системы Оху. Абсциссы точек пересечения с осью Ох (у=0) определяются из уравнения:

3х²+4х−1=0.

Отсюда

Ординаты точек пересечения с осью Оу (х=0) определяются из уравнения:

3у²+4у−1=0.

Аналогично

Итак, эллипс пересекает оси старой системы координат в точках (−1.5;0), (0.2;0), (0;−1.5), (0;0.2).

На осях канонической системы откладываем полуоси эллипса и через восемь точек проводим искомую кривую.

Пример 2. Преобразовать к каноническому виду уравнение и построить кривую

3x²−2√3∙xy+y²+6x+2√3∙y−4=0.

Решение. По условию задачи А=3, В=−√3, С=1, D=3, Е=√3, F=−4. По формуле (2) имеем tgα=√3 и tgα=−√3/3 . Возьмем α=π/3. После вычисления коэффициентов получим

4Y²+6X−2√3∙Y−4=0.

Поскольку Е₁ ≠ 0, то это уравнение можно разрешить относительно Х:

X=

Имеем параболу. Сделаем параллельный перенос по формулам X=x₀+x', Y=y₀+y',

где

Точка O'(x₀, y₀) является началом новой системы координат O'x'y'. Уравнение кривой в этой системе

Сделаем рисунок. Строим систему координат Оху. Находим в этой системе координаты точки О' по формулам поворота осей

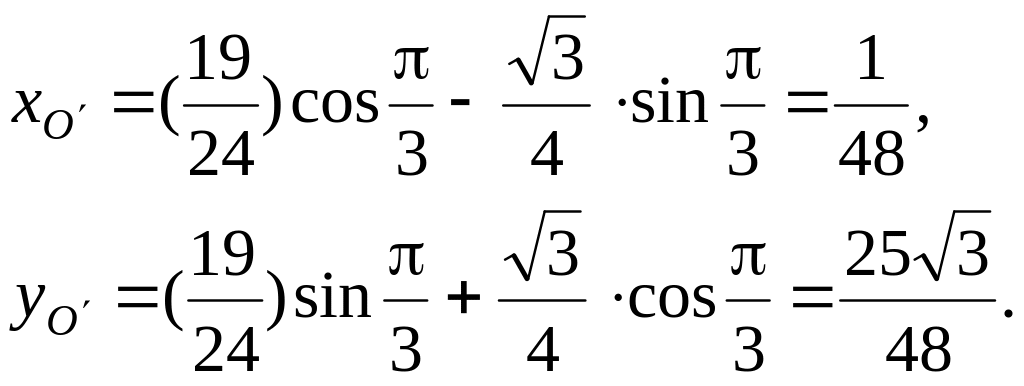
Проводим через точку О' ось х' новой (канонической) системы координат под углом α=π/3 к оси Ох. Направление оси О'у' находим путем поворота оси О'х' на угол 90^о против хода часовой стрелки.

Определяем координаты точек пересечения (если они есть) параболы с координатными осями исходной системы Оху. Абсциссы точек пересечения с осью Ох (у=0) определяются из уравнения:

3x² +6x −4=0.

Отсюда

Ординаты точек пересечения с осью Оу (х=0) определяются из уравнения:

y²+2√3∙y−4=0.

Аналогично

Итак, парабола пересекает оси старой системы координат в точках (−2.5;0), (0.5;0), (0;−4.4), (0;0.9).

Через начало канонической системы и точки пересечения проводим искомую кривую.

Задание 4.

Построение графика функции

r = f(φ)

осуществляют так: а) строят для функции r = f(φ) соответствующую функцию у=f(х); б) исследуют функцию r = f(φ), сравнивая ее с соответствующей функцией у=f(х), учитывая особенности полярной системы координат; в) выполняют построение графика функции r = f(φ) по графику функции у=f(х).