В общем случае это неравенство сходимости можно представить в виде:
, (2.4)
где и – некоторые числа, значения которых определяются методом уточнения корня. Главным показателем скорости сходимости метода является значение , называемое порядком сходимости
14.Одномерная минимизация. Глобальный и локальный минимум (максимум). Простейшие подходы к решению задач минимизации. Метод золотого сечения («золотого сечения»). Априорные и апостериорные оценки погрешности, скорость сходимости.
Минимизация – оптимизация некоторой характеристики f(x), f(x) – целевая функция. Если варьируется один скалярный вектор x, возникает одномерная минимизация.
Глобальный и локальный минимум (минимумы функций на всей длине и на отрезке соответственно)
Унимодальная функция (функция, у которой тока 1 минимум, парабола например, и притом этот минимум может быть на концах графика)
Большинство задач минимизации осуществляет лишь поиск локального минимума через систему нелинейных уравнений.
Метод золотого сечения
Тогда для того, чтобы найти
определённое значение этой функции на
заданном отрезке, отвечающее критерию
поиска (пусть это будет минимум),
рассматриваемый отрезок делится в
пропорции золотого сечения в обоих
направлениях, то есть выбираются две
точки
и
такие,
что:
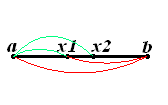
Иллюстрация выбора промежуточных точек метода золотого сечения.
,
где
—
пропорция золотого
сечения.
Таким образом:
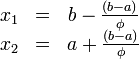
То есть точка
делит
отрезок
в
отношении золотого сечения. Аналогично
делит
отрезок
в
той же пропорции. Это свойство и
используется для построения итеративного
процесса.
Алгоритм
На первой итерации заданный отрезок делится двумя симметричными относительно его центра точками и рассчитываются значения в этих точках. После чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поиска минимума), отбрасывают. На следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку. Процедура продолжается до тех пор, пока не будет достигнута заданная точность.
Формализация
Шаг 1. Задаются начальные границы отрезка
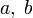и
точность
.Шаг 2. Рассчитывают начальные точки деления:
и
значения в них целевой
функции:
.
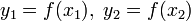Если
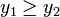(для
поиска max изменить неравенство на
),
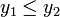то
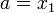
Иначе
.
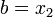Шаг 3.
Если
,
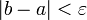то
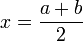и
останов.Иначе возврат к шагу 2.
Определение 4.7 Оценка погрешности, которая находится до решения задачи, называется априорной.
Такую оценку дает теорема о погрешности.
Определение 4.8 Оценка погрешности, которая находится после решения задачи, называется апостериорной.
Эту оценку дает правило Рунге.
РУНГЕ ПРАВИЛО
- один пз методов оценки погрешности формул численного интегрирования. Пусть - остаточный член формулы численного интегрирования, где h - длина отрезка интегрирования или какой-то его части, k - фиксированное число и М - произведение постоянной на производную подинтегральной функции порядка k-1 в какой-то точке промежутка интегрирования. Если J - точное значение интеграла, а I - его приближенное значение, то
Согласно Р. п. вычисляется тот же самый интеграл по той же формуле численного интегрирования, но вместо hберется величина h/2. При этом, чтобы получить значение интеграла по всему отрезку, формула интегрирования применяется дважды. Если производная, входящая в М, меняется не сильно на рассматриваемом промежутке, то
где I1 - значение интеграла, вычисленное по h/2.