1. Вычисления с конечной точностью и их особенности. Абсолютная (предельная абсолютная) и относительная (предельная относительная) погрешности. Источники возникновения погрешностей в вычислительной математике. Погрешности арифметических операций и погрешность вычисления функции.

Любое приближенное вычисление связано с ошибкой (погрешностью).

Виды ошибок:

1. Погрешность математической модели, связанная с неполными знаниями о процессе.

2. Погрешность упрощения модели.

3. Погрешность, связанная с приближенным характером начальных данных.

4. Погрешность приближения.

Первые две погрешности относятся к систематическим, а две последние – к статистическим.

Абсолютные и относительные погрешности.

Абсолютная (предельная) погрешность определяет интервал, в котором лежит точное значение величины.

Пусть А – точное значение величины (оно нам неизвестно). а – приближенное значение величины (известно). За абсолютную погрешность Δ принимается минимальное число Δа, удовлетворяющее условию: Δ≥|А-а|.

При статических измерениях погрешность Δа задается с определенной достоверностью, т.е. вероятность события |А-а|≤ Δа больше определенной величины γ: P(|A-a|≤ Δa)≥ γ≤1

Перепишем определение: а- Δа≤А≤а+ Δа; точное значение А лежит в заданном интервале.

Для оценки качества измерений вводится относительная погрешность

Заданные величины Δа и δа позволяют записать точное значение А в символическом виде: А=а(1± δа)

Погрешность функций.

Пусть дана функция от n приближенных значений , погрешности которых известны. Требуется определить погрешность функции 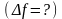. , где - абсолютная погрешность приближенной величины . Если , то разность, стоящую в формуле можно оценить в линейном приближении:

Отсюда следует оценка погрешности:

,

Погрешность простейших функций двух переменных

Погрешность суммы:

Погрешность разности: При 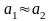качество измерений разности ухудшается.

Замечание: Абсолютная погрешность суммы и разности n приближенных величин равна сумме их абсолютных погрешностей.

Погрешность произведения:

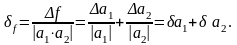
То есть предпочтительней сначала найти относительную погрешность, а затем искать абсолютную: Замечания:

• Относительная погрешность степени есть произведение модуля показателя на относительную погрешность основания степени: .

• Относительная погрешность произведения n сомножителей приближенных величин равна сумме относительных погрешностей сомножителей: . Погрешность частного:

Все замечания сделанные для произведения справедливы и в этом случае.

2. Решение систем линейных уравнений методом Гаусса. Метод исключения Гаусса без выбора ведущего элемента, возможность роста погрешности. Схемы с частичным и полным выбором ведущего элемента. Количество операций для рассматриваемых алгоритмов.

   Метод Гаусса (Метод исключений)

Численное решение систем вида:

(1)

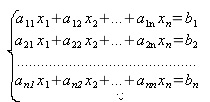
или Ax=b методом Гаусса заключается в последовательном исключении неизвестных. Система (1) поэтапно приводится к треугольному виду. Сначала исключается x1 из 2-го, 3-го, ..., n-го уравнений, для этого необходимо сложить уравнения 2,3,...,n с первым уравнением, умноженным на -a21/a11, -a31/a11,..., -an1/a11 соответственно .

(2)

Потом x2 из 3-го,..., n-го умножением второго уравнения на -a¹32/a¹22, -a¹42/a¹22,...,

-a¹n2/a¹22 и сложением с 3,4,..n уравнениями.

И дальше по аналогии система приводится к треугольному виду:

процесс приведения системы к треугольному виду называется прямым ходом. Общие фомулы для прямого хода:

k =1,...,n – 1; i,j = k+1,...,n .

Для нахождения решения теперь необходимо вычислить неизвестные, начиная с n-го уравнения. Процесс вычисления значений неизвестных называется обратным ходом.

На каждом этапе xk находится по формуле

k = n, n-1, ..., 1.

Один из основных недостатков метода Гаусса связан с тем, что при его реализации накапливается вычислительная погрешность. В книге [ Самарский , Гулин] показано, что для больших систем порядка m число действий умножений и делений близко к .

Для того, чтобы уменьшить рост вычислительной погрешности применяются различные модификации метода Гаусса. Например, метод Гаусса с выбором главного элемента по столбцам, в этом случае на каждом этапе прямого хода строки матрицы переставляются таким образом, чтобы диагональный угловой элемент был максимальным. При исключении соответствующего неизвестного из других строк деление будет производиться на наибольший из возможных коэффициентов и следовательно относительная погрешность будет наименьшей.

Существует метод Гаусса с выбором главного элемента по всей матрице. В этом случае переставляются не только строки, но и столбцы¹. Использование модификаций метода Гаусса приводит к усложнению алгоритма увеличению числа операций и соответственно к росту времени счета. Поэтому целесообразность выбора того или иного метода определяется непосредственно программистом².

Выполняемые в методе Гаусса преобразования прямого хода, приведшие матрицу А системы к треугольному виду позволяют вычислить определитель матрицы

.

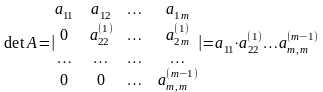Метод Гаусса позволяет найти обратную матрицу. Для этого необходимо решить матричное уравнение

,

где Е единичная матрица. Его решение сводится к решению m систем

у вектора j –я компонента равна единице, а остальные компоненты равны нулю.

Метод Гаусса-Жордана для решения системы уравнений

Метод Гаусса-Жордана является еще одной вариацией метода Гаусса для решений систем уравнений. Его отличием является отсутствие обратного хода, но при этом количество действий, выполняемых для решения системы увеличивается. Рассмотрим следующую систему уравнений 3-го порядка:

Первым этапом производится нормирование первого уравнения, далее исключается переменная x1. Отличием является то, что выражение для xkподставляется во все уравнения кроме k-го (с ведущим элементом). Далее действия повторяются и исключается вторая переменная, а затем и третья.

Нормирование 1-го уравнения, исключение x1,

Нормирование 2-го уравнения, исключение x2

Нормирование 3-го уравнения, исключение x3

Достоинством метода Гаусса-Жордана является простота программирования за счет отсутствия обратного хода.

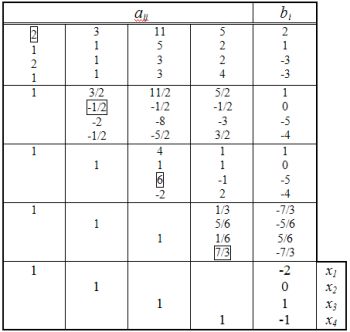
Табличное представление решения системы уравний методом Гаусса-Жордана.