В общем случае это неравенство можно представить в виде:

 

, (2.4)

 

где и – некоторые числа, значения которых определяются методом уточнения корня. От значений q и  зависит насколько с каждым шагом уменьшается погрешность приближенных значений и, соответственно, насколько быстро можно получить приближенное значение с заданной точностью. Главным показателем скорости сходимости метода является значение , называемое порядком сходимости

Метод бисекции (он же дихотомии и половинного деления)

Считаем, что отделение корней уравнения (2.1) проведено и на отрезке расположен один корень, который необходимо уточнить с погрешностью . В качестве начального приближения корня принимаем середину этого отрезка: (рис. 2.5). Затем исследуем значение функции на концах отрезков и . Тот из отрезков, на концах которого принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка (на рис. 2.5 это отрезок ). Вторую половину отрезка , на которой не меняет знак, отбрасываем. В качестве следующего приближения корня принимаем середину нового отрезка и т.д. Таким образом, k-е приближение вычисляется как

 

После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k итераций в раз: 

Критерий окончания итерационного процесса: если длина отрезка локализации меньше 2 , то итерации прекращают и в качестве значения корня с заданной точностью принимают середину отрезка.

 

Теорема о сходимости метода бисекций. Пусть функция f(x) непрерывна на [a,b] и на концах принимает значения разных знаков .Тогда метод сходится и справедлива оценка погрешности :

Метод простых итераций

Для применения метода простой итерации следует исходное уравнение преобразовать к виду, удобному для итерации . Это преобразование можно выполнить различными способами. Функция называется итерационной функцией. Расчетная формула метода простой итерации имеет вид: .

Теорема о сходимости метода простой итерации. Пусть в некоторой - окрестности корня функция дифференцируема и удовлетворяет неравенству , где - постоянная . Тогда независимо от выбора начального приближения из указанной - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится

со скоростью геометрической последовательности и справедлива оценка погрешности: , .

Критерий окончания итерационного процесса. При заданной точности >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство 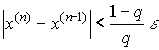. Если величина , то можно использовать более простой критерий окончания итераций:

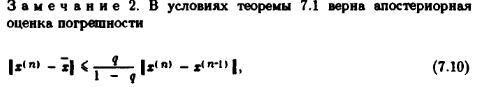(x с чертой – решение в какой либо окрестности, 0<=q<1)

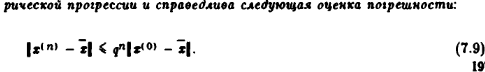(априорная)

Графически:

В начале рассмотрим графически процесс получения приближений в методе простых итераций (рис. 2.11). При решении уравнения (2.21) необходимо отыскать точку пересечения кривой и прямой . На рисунке 2.11, (а) изображена некоторая кривая , которая может представлять собой любую функцию, но сейчас для нас важно то обстоятельство, что производная этой функции в окрестности корня положительна и меньше 1. Пусть – корень уравнения, который, естественно, предполагается неизвестным. Выберем начальное приближение в точке . Следующее приближении , в соответствии с (2.22), будет равно . Для того, чтобы отобразить на графике можно провести через точку прямую, параллельную оси OX, до пересечения с прямой , а затем в точке пересечения этих прямых опустить перпендикуляр на ось OX, который и отметит положение точки . Аналогично получаются все последующие приближения.

Метод Ньютона (метод касательных) . Расчетная формула метода Ньютона имеет вид:

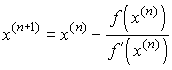
Геометрически

Пусть нам известно начальное приближение к корню (вопрос выбора начального приближение будет подробно рассмотрен ниже). Проведем в этой точке касательную к кривой (рис. 2.8). Эта касательная пересечет ось абсцисс в точке , которую будем рассматривать в качестве следующего приближения

Теорема о сходимости метода Ньютона. Пусть - простой корень уравнения , в некоторой окрестности которого функция дважды непрерывно дифференцируема. Тогда найдется такая малая - окрестность корня , что при произвольном выборе начального приближения из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка

, где , .

 

Критерий окончания итерационного процесса. При заданной точности >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство .

Метод сечений (вроде второе название метод хорд, но не точно)

Расчетная формула

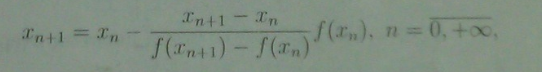
Тут я опишу для метода хорд (вроде тоже самое, честно хз, расчетные формулы похожи)

Графически

Рассматриваемый метод так же, как и метод половинного деления, предназначен для уточнения корня на интервале , на концах которого функция принимает значения разных знаков. Очередное приближение в отличие от метода половинного деления берем не в середине отрезка, а в точке , где пересекает ось абсцисс прямая линия (хорда), проведенная через точки А и В (рис. 2.6).

Критерий окончания