Зразок виконання індивідуальних завдань. Диференціальне числення функцій однієї змінної

Задача 1. Знайти похідну першого порядку заданої функції

, ; ; .

Розв’язання

1). Користуючись правилами диференціювання складної функції та таблицею похідних, маємо

.

2). Користуючись правилами диференціювання складної функції, маємо

.

3). Представимо функцію у вигляді, що дає можливість застосувати правило диференціювання складної функції, маємо

,

.

4). Диференціюємо співвідношення , розглядаючи як функцію від :

.

Розв’яжемо одержане рівняння відносно :

.

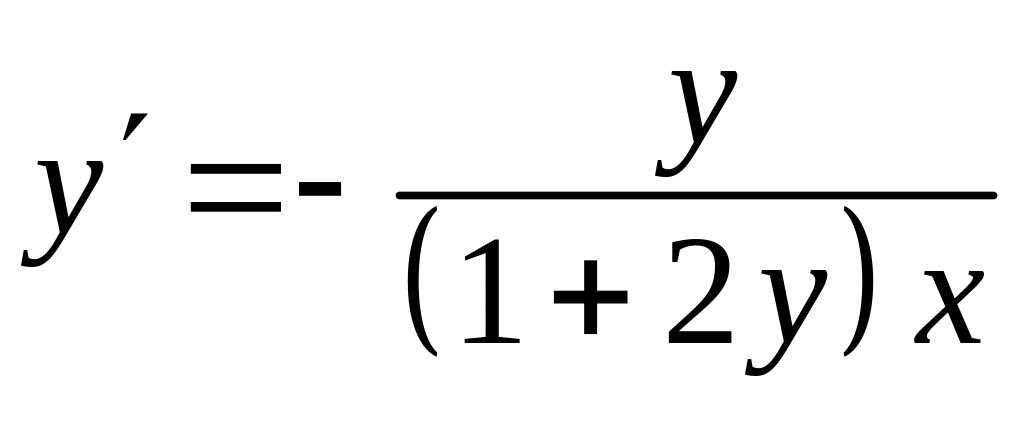Задача 2. Знайти похідні та диференціали першого та другого порядків заданої функції

.

Розв’язання

Знайдемо першу похідну заданої функції, користуючись правилами диференціювання складної функції. Маємо

.

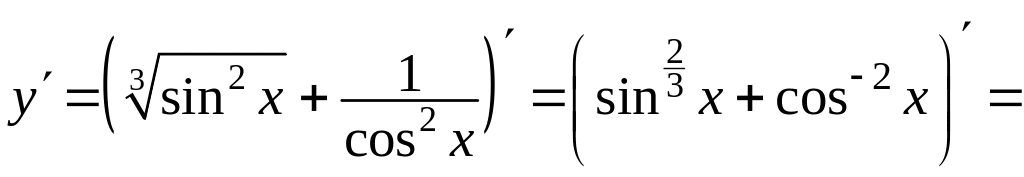
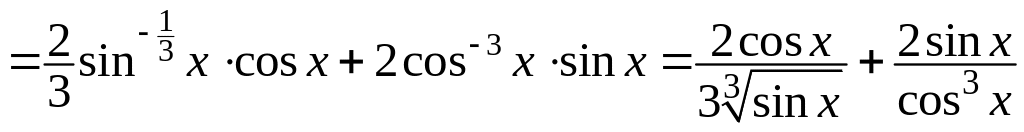Диференціал першого порядку знайдемо за формулою . Підставляючи знайдену вище похідну, маємо

.

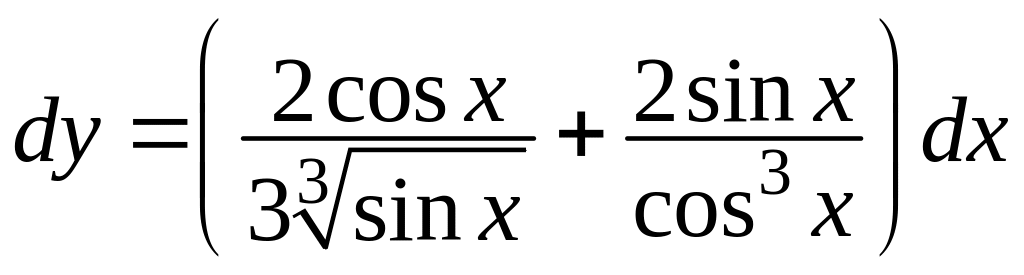Знайдемо похідну другого порядку заданої функції:

.

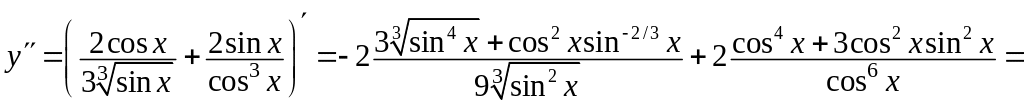
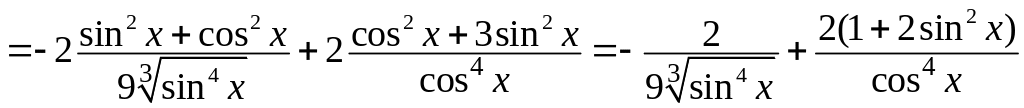Диференціал другого порядку знайдемо за формулою :

.

Задача 3. Скласти рівняння дотичної до кривої у точці з абсцисою .

Розв’язання

Диференціюємо функцію, користуючись таблицею похідних .

Обчислюємо . Обчислюємо . Рівняння дотичної до кривої:

.

Підставляючи числові значення, дістанемо:

або .

Задача 4. Скласти рівняння дотичної до криво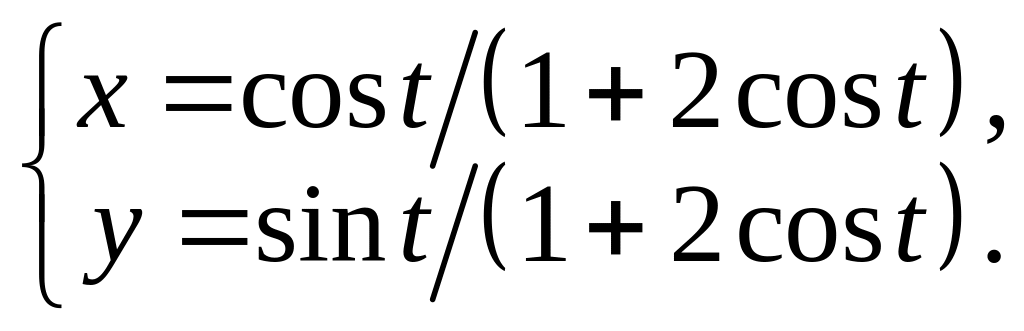ї у точці .

Розв’язання

Похідна функції, заданої параметрично, обчислюється за формулою . Знайдемо спочатку

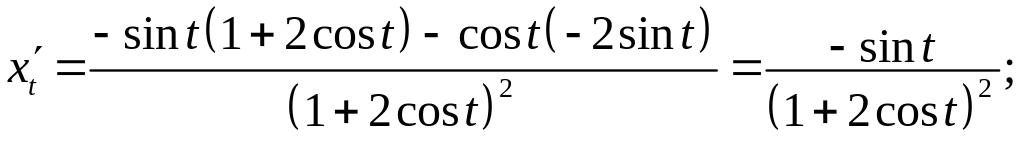
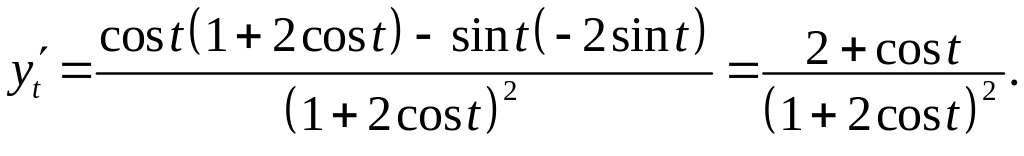
Тоді

.

Далі обчислимо

.

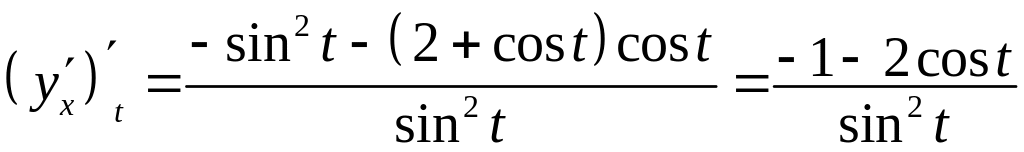Другу похідну знайдемо за формулою 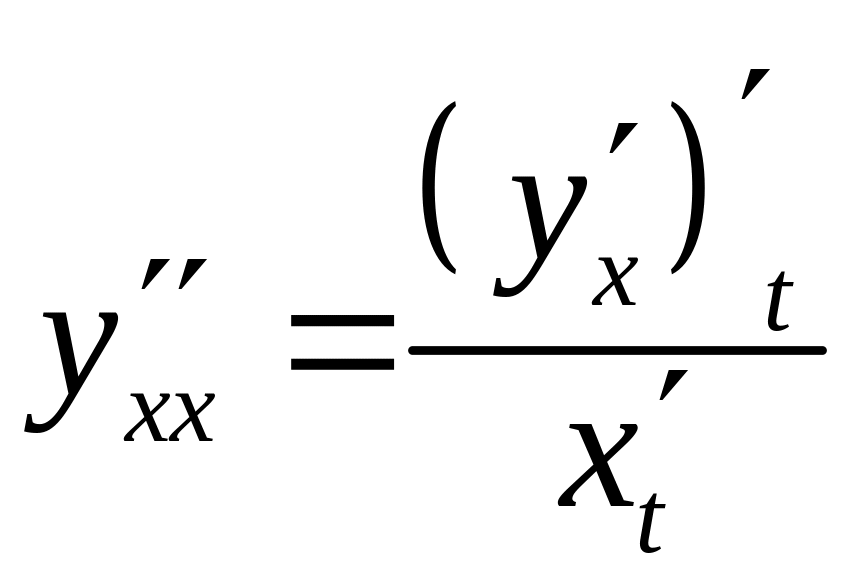. Отже,

.

Рівняння дотичної до кривої має вигляд:

.

Знайдемо

. ,

, .

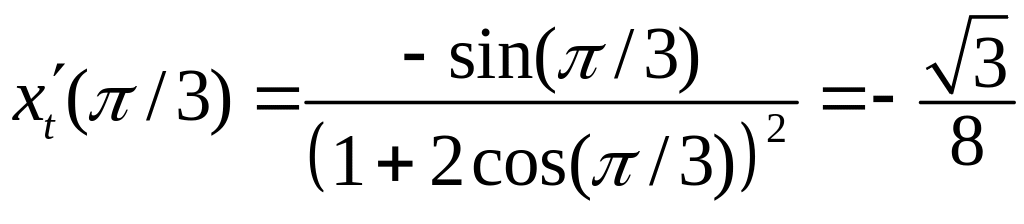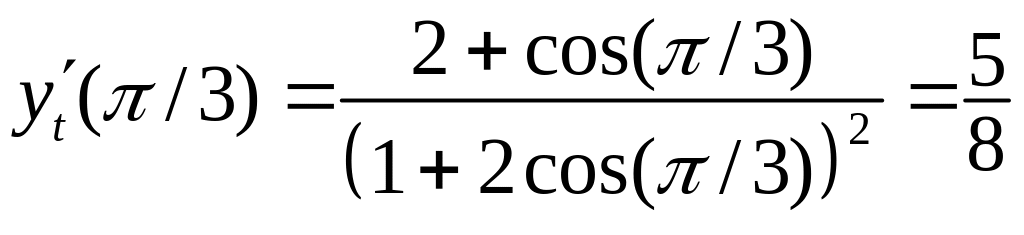Підставляючи числові значення у рівняння дотичної, дістанемо:

.

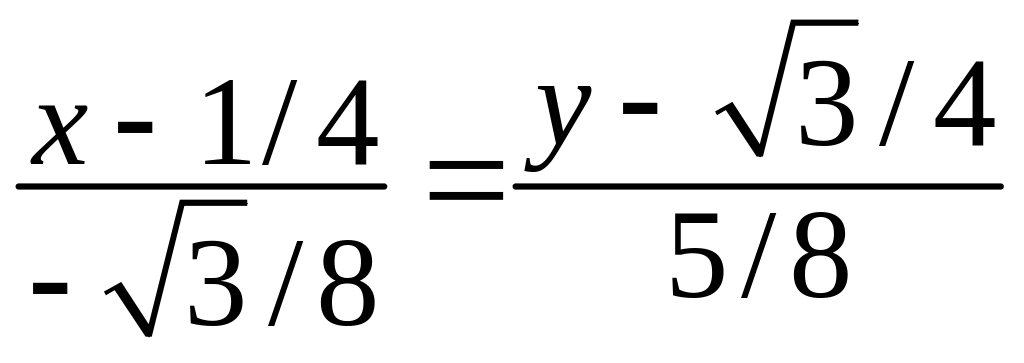Задача 5. Обчислити границі функцій, користуючись, коли це можливо, правилом Лопіталя.

; ; ; .

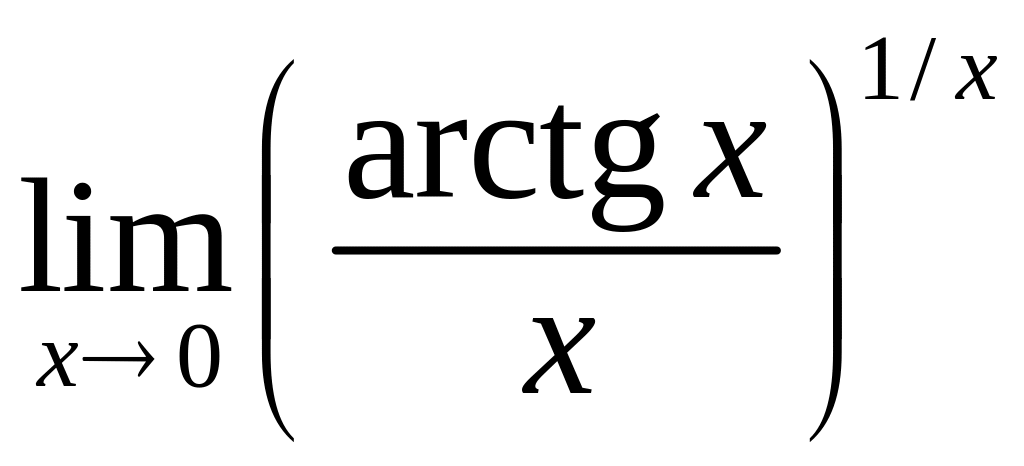Розв’язання

1). Маємо невизначеність . Застосовуючи правило Лопіталя, дістанемо:

.

Знов маємо невизначеність . Застосовуємо ще раз правило Лопіталя:

.

2). Маємо невизначеність . Представимо функцію у вигляді дробу:

.

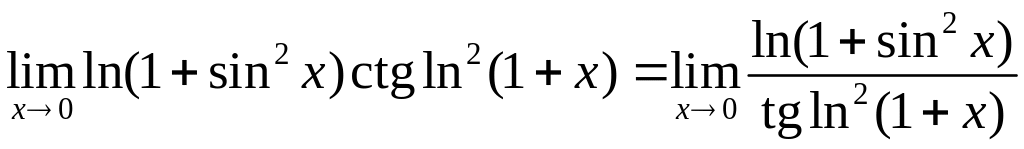Тепер ми маємо невизначеність , до якої застосуємо правило Лопіталя:

.

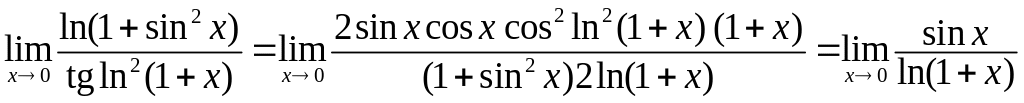Застосувавши ще раз правило Лопіталя, остаточно дістанемо:

3). Маємо невизначеність . Представимо функцію у вигляді

.

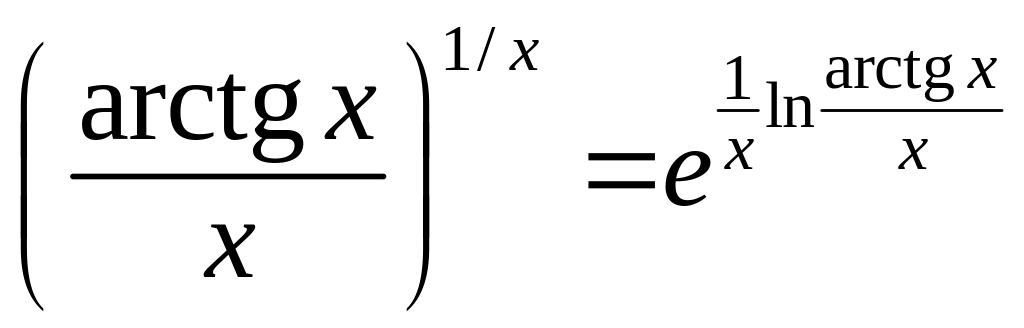Перейдемо до границі у показнику степеня, користуючись правилом Лопіталя:

.

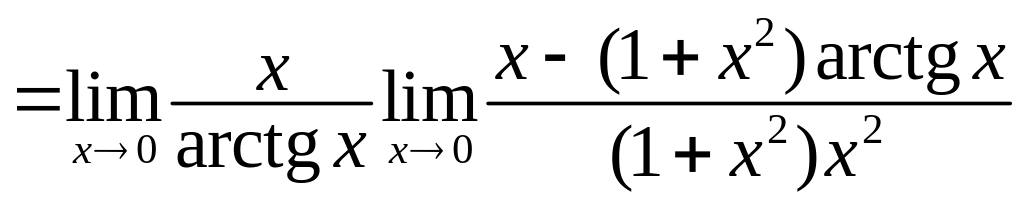Враховуючи, що за наслідком з першої визначної границі , маємо:

.

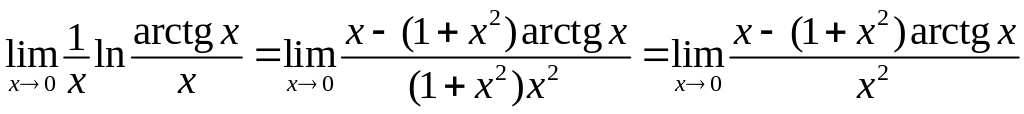Отриману невизначеність вигляду , розкриваємо за правилом Лопіталя:

.

Остаточно дістанемо

.

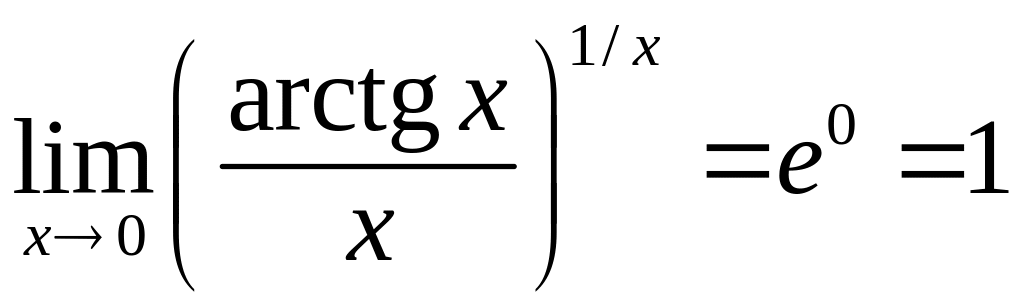4). Маємо невизначеність , до якої неможна застосувати правило Лопіталя, бо границя похідної знаменника дробу не існує. Розділимо чисельник і знаменник дробу на

.

Враховуючи, що та за теоремою про добуток обмеженої функції на нескінченно малу, маємо:

.

Задача 6. Знайти найбільше і найменше значення функції на відрізку .

Розв’язання

Знайдемо першу похідну:

.

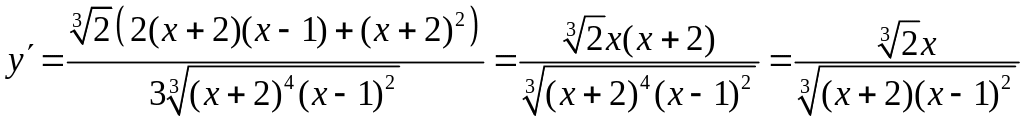Критичними точками є , та , бо в цих точках похідна дорівнює нулю або не існує. Функція може приймати найбільше та найменше значення на відрізку у точках екстремуму, якщо вони належать відрізку, або на кінцях відрізка. Усі критичні точки належать відрізку . Обчислимо значення функції у критичних точках та на кінцях відрізку:

, , , , .

Отже, свого найбільшого значення функція досягає у точці , а найменшого відразу у двох точках: та .

Задача 7. З квадратного листа картону зі стороною а вирізують по кутах однакові квадрати. З решти листа склеюють прямокутну коробку. Яка має бути сторона вирізаного квадрата, щоб об’єм коробки був найбільшим?

Розв’язання

Позначимо через сторону вирізаного квадрата. Одержана коробка буде мати висоту . Її основою буде квадрат зі стороною . Отже, об’єм коробки . Дослідимо цю функцію на екстремум, для чого знайдемо її похідну:

.

Функція має дві стаціонарні точки та . Для визначення характеру екстремуму знайдемо другу похідну та її значення у стаціонарних точках:

.

Значення другої похідної у точці від’ємне, тому ця точка є точкою максимуму функції. Таким чином, коробка буде мати найбільший об’єм, якщо вирізати квадрат зі стороною .

Задача 8. Побудувати графік функції за допомогою похідної першого порядку.

Розв’язання

Функція визначена на всій числовій осі. Знайдемо її похідну:

.

Рівняння має два розв’язки та , які є стаціонарними точками функції. Для визначення точок екстремуму та інтервалів монотонності складемо таблицю:

	+	0	–	0	+
		Локальний максимум		Локальний мінімум

Обчислимо значення функції у точках екстремуму .

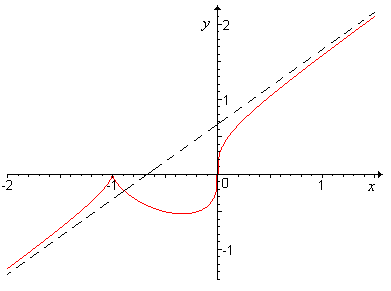
За даними дослідження будуємо графік функції.

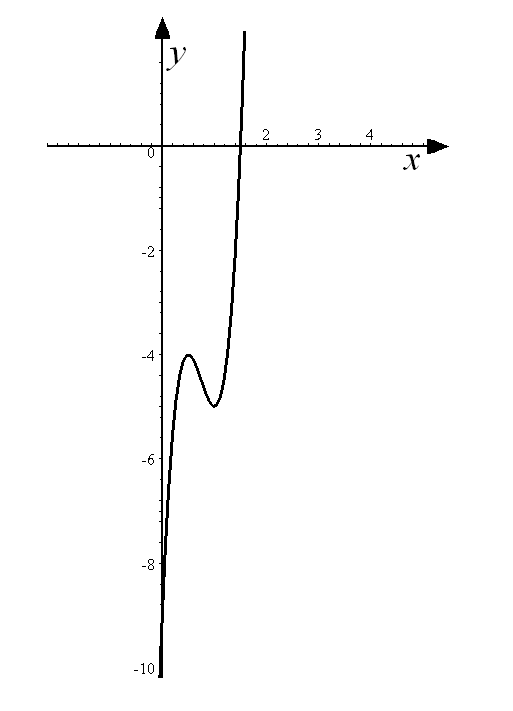
Задача 9. Провести повне дослідження та побудувати графік функції .

Розв’язання

Функція визначена і неперервна на всій числовій осі.

Знайдемо точки перетину графіка функції з осями координат. При перетині з віссю Ох ( ) маємо рівняння , звідки або . Отже, графік функції перетинає вісь Ох у точках та . З метою визначення точок перетину графіка з віссю Оу покладемо . Маємо . Графік функції проходить через початок координат та точку .

Функція не є ні парною, ні непарною, бо , що не дорівнює ні , ні .

Знайдемо проміжки знакосталості функції: для усіх та для усіх .

Визначимо проміжки монотонності і знайдемо точки екстремуму функції. Для всіх и маємо

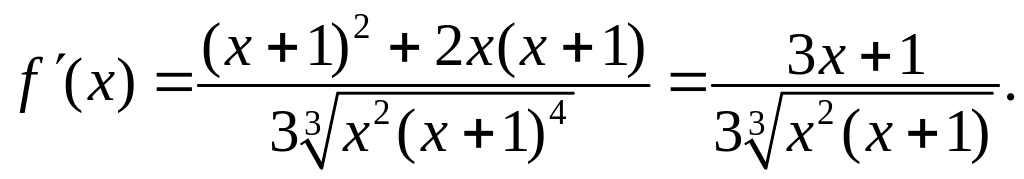
Рівняння має єдиний розв’язок , тому стаціонарна точка . Похідна не існує в точках та , отже, критичні точки , , .

Оскільки для і для , то функція зростає на проміжках та спадає на проміжку .

У точці функція досягає мінімуму . У точці функція досягає максимуму .

Зведемо одержані результати у таблицю

						0
	+	Не існує	–	0	+	Не існує
		Локальний максимум		Локальний мінімум

Визначимо проміжки опуклості і точки перегину функції. Для та маємо

.

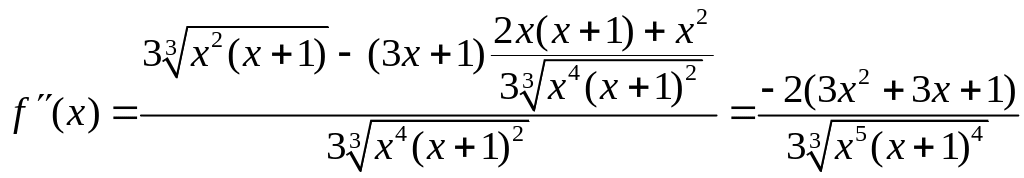Для , тому функція опукла вниз на та . Для , тому функція опукла вверх на . При переході через точку друга похідна змінює знак і при цьому не існує, тому точка є точкою перегину графіка функції.

Складемо ще одну таблицю.

				0
	+	Не існує	+	Не існує	–
				Точка перегину

Вертикальних асимптот графік функції не має, бо функція визначена та неперервна при всіх значеннях аргументу. Рівняння похилих асимптот будемо шукати у вигляді , де

, ,

причому знак “+” беремо для правосторонньої, а “–” для лівосторонньої асимптоти. Знайдемо спочатку рівняння правосторонньої похилої асимптоти. Для цього обчислимо и :

;

.

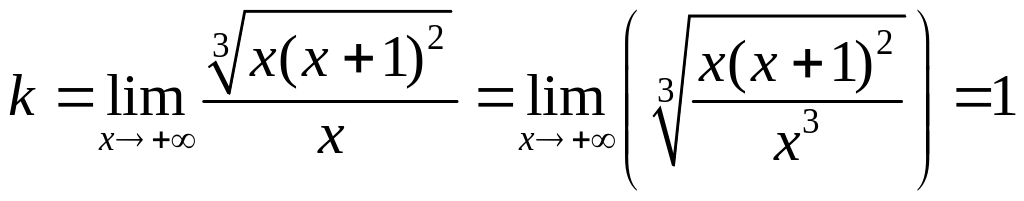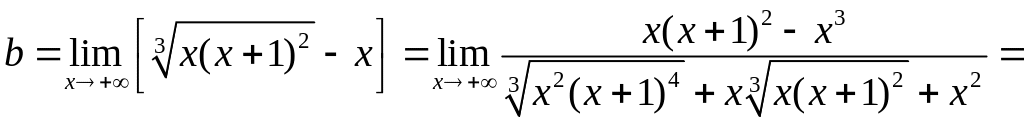
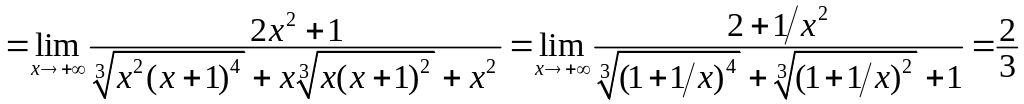Рівняння правосторонньої асимптоти . Для лівосторонньої асимптоти також та , отже її рівняння .

За даними дослідження будуємо графік функції.