Энергия в колебательных процессах

Механическая энергия тела, как известно, складывается из кинетической и потенциальной. Кинетическая энергия максимальна в точке равновесия и убывает при отклонении. В точке максимального отклонения она равна нулю. По закону сохранения потенциальная энергия в точке x=A максимальна. В точке равновесия она принимается равной нулю.

Вычислим компоненты энергии пружинного маятника. Опустим для простоты параметр .

.

. .

Полная энергия .

Учитывая, что ²=k/m, придем к выводу, что полная энергия W=kA²/2 сохраняется.

Часто используют понятие средней кинетической и средней потенциальной энергии за период колебаний. Расчет показывает

.

В колебательном контуре полная энергия складывается из энергии электрического поля в конденсаторе и энергии магнитного поля катушки

.

Первую можно уподобить потенциальной энергии, вторую — кинетической. В самом деле: электрическое поле в конденсаторе потенциальное, а магнитное поле связано с движением зарядов.

Общая закономерность: энергия в колебательном процессе пропорциональна квадрату амплитуды колебаний.

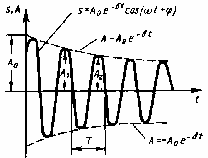
Затухающие колебания

В реальных колебательных процессах присутствуют силы сопротивления, а значит, существуют энергетические потери. Сила сопротивления при малых скоростях пропорциональна скорости: .

Для пружинного маятника

или .

Обычно дифференциальное уравнение затухающих колебаний записывают в виде

(8) .

Параметр  является коэффициентом затухания. Параметр ₀ в гармоническом колебании играл роль циклической частоты. Однако мы можем ожидать, что у затухающих колебаний частота имеет другое значение. Строго говоря, затухающие колебания не являются периодическими: , поскольку убывает амплитуда.

Будем искать решение в виде

.

Выразим скорость и ускорение:

, .

После подстановки этих выражений в (5) и преобразований получим

.

Решением этого уравнения будет синусоида , где циклическая частота . А закон затухающих колебаний принимает вид

(9) .

Отношение

показывает, во сколько раз амплитуда колебаний уменьшается за 1 период. Оно называется декрементом затухания. Величина — логарифмический декремент затухания. Промежуток времени =1/, за который амплитуда уменьшается в e раз, называется временем релаксации.

Вынужденные колебания. Резонанс

Колебательный процесс, протекающий под действием внешней, периодически изменяющейся силы, называется вынужденным колебанием. Приложенную силу называют вынуждающей силой. Пусть она изменяется во времени по закону .

Дифференциальное уравнение колебательного процесса

или

,

где .

Из теории дифференциальных уравнений известно, что решением этого уравнения будет сумма двух колебаний — свободных затухающих и колебаний с частотой изменения вынуждающей силы. Первое слагаемое играет сколь-нибудь заметную роль только в начале процесса. Амплитуда второго возрастает, стремится к некоторому пределу A. Таким образом устанавливаются колебания

.

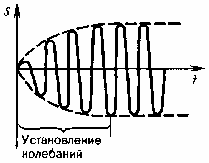
Установившуюся в конце концов амплитуду можно вычислить подстановкой x, v, a в дифференциальное уравнение. Приведем это значение

(10) .

Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных ₀ и ) амплитуда зависит от частоты вынуждающей силы. При некотором значении частоты амплитуда колебаний достигает максимального значения. Это явление называется резонансом.

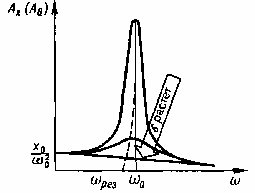
Частота, при которой амплитуда максимальна, называется резонансной частотой. Расчеты дают значения резонансной частоты и амплитуды.

(11) ;

(12) .

Из последней формулы видно, что при отсутствии сопротивления амплитуда обратилась бы в бесконечность.