18. Проверка качества генерируемых последовательностей

Качество генерируемых последовательностей определяется их статистическими свойствами, а именно случайностью получаемых чисел, их равномерной распределенностью в интервале (0,1) и независимостью. Поэтому все последовательности псевдослучайных чисел, полученные с программ-генераторов, должны быть проверены с помощью специальных тестов на случайность, равномерность и некоррелированность. В основе многих тестов проверки качества получаемых последовательностей лежит критерий ² Пирсона, позволяющий проверить соответствие эмпирического распределения случайной величины X и предполагаемого теоретического. Схема применения критерия следующая. Выборка объема n из значений случайной величины X разбивается на  интервалов одинаковой длительности. Затем определяются значения n_i - количество попаданий величины X в i-ый из разрядов. С помощью таблиц вычисляется значение p_i теоретической вероятности попадания случайной величины в i-ый интервал. Далее подсчитывается наблюдаемое значение критерия по формуле:

,

Известно, что случайная величина ² распределена по закону ² с числом степеней свободы k, где  - число разрядов выборки, а k -число неизвестных параметров предполагаемого распределения. Критическая область для критерия – правосторонняя. Критическая точка ²_кр определяется из таблиц ² - распределения по уровню значимости  и числу степеней свободы исходя из условия

P(² >²_кр )=.

Если >²_кр , то гипотеза о соответствии распределений отвергается. Если <²_кр , то она не противоречит опытным данным.

Проверка случайности. Для того, чтобы проверить, насколько хорошо генерируемая последовательность имитирует последовательность случайных чисел, наиболее часто используется тест серий. С его помощью проверяется один из разрядов (обычно старший) чисел полученной последовательности. При более тщательной проверке исследуются независимо друг от друга несколько старших разрядов.

Пусть получена последовательность x₁ ,..., x_n псевдослучайных чисел из интервала (0,1). Обозначим символами ₁ ,..., _n цифры старшего разряда чисел последовательности. Цифры _k+1,...,_k+ образуют серию длины , если _k+1 =_k+2 =...= _k+._k++1 . Количество серий длины  во всей последовательности обозначим K_ (=1,n), а общее число серий

.

Известно, что длина  последовательности подчинена биномиальному закону. Для того, чтобы установить случайность последовательности, нужно проверить гипотезу о законе распределения с помощью одного из критериев (тестов) согласия, например ².

Критерий ² в данном случае имеет следующий вид:

.

При этом

p_=P(_k+1 =_k+2 =...= _k+._k++1)=9*10^- .

Так как, начиная с некоторой длины m серии с длиной, большей m, встречаются мало, то все серии длины m+1 объединяют в одну группу. Число серий этой группы обозначим K_m+1 . Получено p_m+1=10^-m , а критерий ² принимает вид:

.

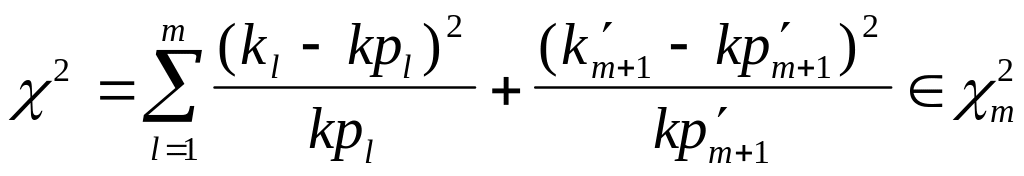П роверка равномерности. Для проверки гипотезы о равномерности распределения псевдослу­чайных чисел в интервале (0,1) обычно используется так называемый частотный тест. При этом гипотеза равномерности проверяется критерием . Интервал (0,1) разбивается на m равных интервалов. Да­лее определяется количество чисел , попавших в i -ыи интервал. Так как предполагаемое распределение равномерно, т.е. теоретические вероятности попадания в i- ый интервал равны , критерий можно записать в следующем виде:

.

Здесь n -число элементов исследуемой последовательности.

Проверка независимости. Для практического использования псевдослучайных чисел вполне достаточно их некоррелированности. Некоррелированность случайных чисел можно проверить с помощью коэффициента корреляции:

.

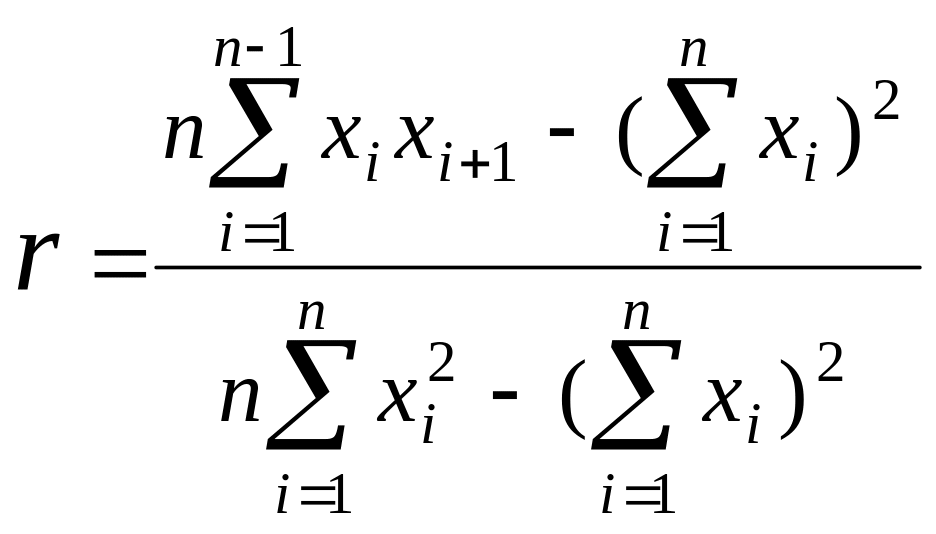Если полученное число близко к 0, то элементы последователь­ности считаются некоррелированными.

Например, если

,

то можно считать, что генератор выдержал тест.

19. Марковские системы и их математические модели

Если некоторая физическая система с течением времени в случайные моменты времени t₁,t₂,...,t_n переходит соответственно в состояния Z₁,Z₂,...,Z_n, то считается, что в системе протекает случайный процесс. Такой случайный процесс называется марковским, если вероятностные характеристики процесса в будущем зависят только от его состояния Z₀ в данный момент времени t₀ и не зависят от того, когда и каким образом система пришла в состояние Z₀. Марковским процесс назван по- имени выдающегося русского математика академика А.А.Маркова, специалиста по теории вероятностей и математическому анализу.

В вычислительном зале имеется две ЭВМ, обслуживающие потоки заявок (пользователей). В дискретные моменты времени t₀,t₁,t₂.. пользователи подходят к ЭВМ. Тогда СМО вычислительный зал-пользователь может находиться в случайные моменты времени t₀,t₁,t₂... в следующих четырех состояниях: Z₀ - обе ЭВМ свободны от пользователей Z₁ - первая ЭВМ обслуживает заявку, а вторая - свободна; Z₂ - вторая ЭВМ обслуживает, а первая - свободна; Z₃ - обе ЭВМ заняты обслуживанием пользователей. Здесь состояния системы заранее известны, их можно перечислить. Переходы из состояния в состояние случайны и могут осуществляться в любой момент времени. Вероятностные характеристики процесса обслуживания пользователей в будущем зависят лишь от состояния системы в данный момент времени (от того, в каком из состояний Z₀,Z₁,Z₂,Z₃ она находится в t₀) и не зависят от прошлого, т.е. от того, когда и как система перешла в данное состояние. Такой процесс можно считать марковским с дискретными состояниями и непрерывным временем существования.

20.

Важным свойством уравнение Колмогорова является следующее: сумма правых частей уравнения равна нулю. Это свойство можно использовать при проверке правильности написания уравнений.

22. Одноканальная СМО с отказами. Наиболее простой системой является одноканальная СМО с отказами – М/М/1. Она имеет один канал обслуживания, входящий поток характеризуется интенсивностью , поток обслуживания – интенсивностью . Основными характеристиками такой системы являются абсолютная и относительная пропускная способность.

Абсолютная пропускная способность – это интенсивность выходящего потока обслуженных заявок (_об).

. Рассматриваемая СМО имеет всего два состояния: Z₀ – система свободна, заявок нет, канал обслуживания простаивает; Z₁ – в системе находится одна заявка, которая занимает канал обслуживания, это состояние занятости системы.

Одноканальная СМО с ожиданием (М/М/1).

Поток входящих заявок пуассоновский с интенсивностью , интенсивность обслуживания .

Такая система может находиться в (n+2) состояниях:

Z₀ – система свободна, очереди нет, канал обслуживания простаивает;

Z₁ – одна заявка находится в канале обслуживания, очереди нет;

Z_n+1 – одна заявка находится в канале обслуживания и в очереди находятся n заявок.

Граф переходов описанной системы показан на рис.3.7.

  . . . . .   . . . . . 

. . . . . . . . .

    

Основные характеристики данной системы:

1. вероятность отказа – это вероятность того, что единственный канал обслуживания и n мест в очереди заняты т.е. это вероятность состояния Z_n+1:

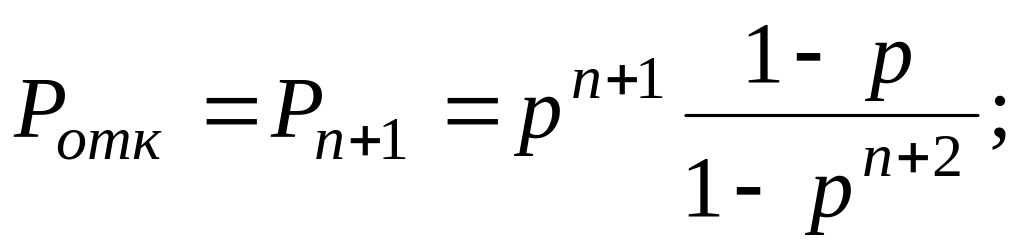
2. вероятность обслуживания или относительная пропускная способность: ;

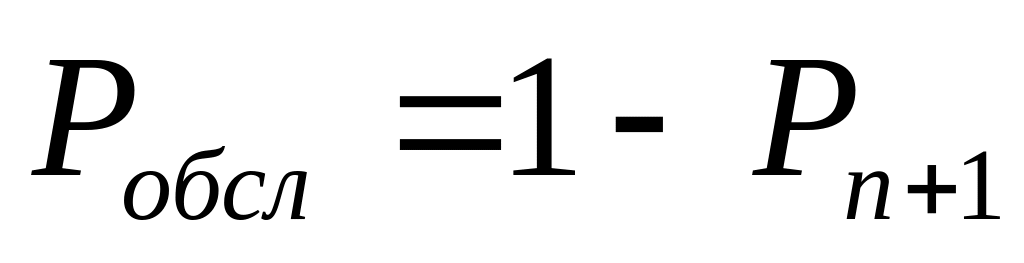3. абсолютная пропускная способность – интенсивность покоя обслуженных заявок: ;

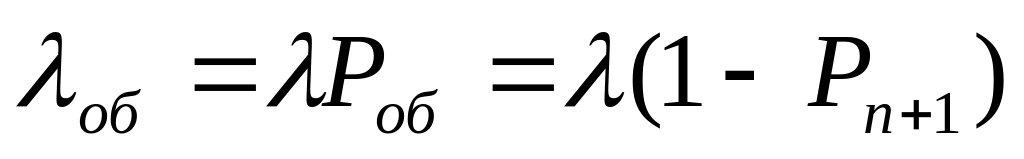4. средняя длина очереди определяется по стандартной формуле для математического ожидания дискретной случайной величины с учётом вероятностей состояний и связи номера состояния с числом мест в очереди:

5. среднее число заявок в системе: ;

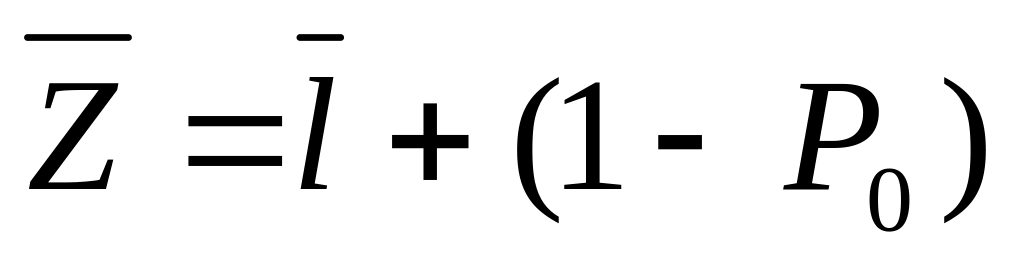6. среднее время ожидания: