1.Перемещение - это вектор, соединяющий начальное и конечное положение точки.

Путь - это расстояние между двумя положениями точки, измеренное вдоль траектории ее движения.

Траектория — непрерывная линия, которую описывает точка при своём движении.

Скорость — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.

Ускорение — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени.

2. Материа́льная то́чка - тело, размерами которого можно принебречь, т. к. они очень малы.

Абсолютно твердое тело – тело, которое ни при каких условиях не деформируется.

Вращательное движение - вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях.

Угловая скорость тела - векторная величина, характеризующая скорость вращения тела.

Угловое ускорение— величина, характеризующая быстроту изменения угловой скорости.

Момент инерции - величина, характеризующая  распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. 

Основной закон динамики вращательного движения твердого тела, вращающегося вокруг точки.

3.Законы Ньютона

Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.

В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. F=ma

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил. производная импульса по времени

Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается: или

Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности.

Нельзя рассматривать частный случай (при F=0) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

3. Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

И́мпульс — векторная физическая величина, характеризующая меру механического движения тела. 

Зако́н сохране́ния и́мпульса утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

До взаимодействия После взаимодействия

Согласно 3 з-ну Ньютона:  , следовательно: 

4. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины и направления силы (сил) и от перемещения точки (точек) тела или системы

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения^[3]:

Мо́щность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Консервативными наз. силы,работа которых не зависит от траектории тела, а опреедляется только начальным и конечным положением тела.(н-р.сила тяжести). Диссипативными силами наз-ся силы ,работа которых зависит от траектории движения.(н-р.все силы трения и сопротивления)

. 

5. К.Э.- энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного ивращательного движения.

П.Э.- механическая энергия системы тел, которая определяется характером сил взаимодействия между ними и их взаимным расположением.  Зако́н сохране́ния эне́ргии-заключается в том, что энергия изолированной физической системы сохраняется с течением времени. Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую.

6. Основной закон динамики вращательного движения:

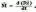
или M=J

Момент силы F материальной точки относительно неподвижной точки О наз-ся физ-ая величина,определяемая векторным произведением радиус вектора r проведённая в т.F на силу F. М=[r,F]

При вращении тела вокруг неподвижной оси момент вокруг этой оси создаёт только одна составляющая действующей на него силы, а именно касательная к траектории точки её преломления.

Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают Момент силы относительно центра (точки) и относительно оси.   Момент силы относительно центра О величина векторная. Его модуль Mo = Fh, где F - модуль силы, a h - плечо, т. е. длина перпендикуляра, опущенного из О на линию действия силы (см. рис.); направлен вектор Mo перпендикулярно плоскости, проходящей через центр О и силу, в сторону, откуда поворот, совершаемый силой, виден против хода часовой стрелки (в правой системе координат). С помощью векторного произведения Момент силы выражается равенством Mo = [rF], где r - радиус-вектор, проведённый из О в точку приложения силы. Размерность Момент силы - L2MT2, единицы измерения - н×м, дин×см (1 н×м = 107дин×см) или кгс×м.   Момент силы относительно оси величина алгебраическая, равная проекции на эту ось Момент силы относительно любой точки Ооси или же численной величине момента проекции Рху силы F на плоскость ху, перпендикулярную оси z, взятого относительно точки пересечения оси с плоскостью. Т. е. Mz = Mo cos g = ± Fxy h1.

7.Момент инерции материальной точки называется физическая величина равная произведению массы материальной точки на квадрат расст-я до рассматривамой оси.

Момент инерции тела относительно неподвижной оси называется физическая величина равная сумме моментов инерции мат. точки, составляющих это толо.

Теорема Штейнера.Момент инерции тела относительно произвольной оси равной моменту его инерции относительно параллельной проходящей через центр масс сложенной с произведением массы тела на квадрат произведения между плоскостями. где J0 - момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси, d - расстояние между осями, m - масса тела.

Таблица.

8. Если тело одновременно учавствует в двух движениях поступательном и вращательном,то полная кинетическая энергия тела складывается из кинетической энергии поступательного и вращательного движения. T=mv/2+

Кинетическая энергия вращения Возьмем абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 1). Разобьем тело на маленькие объемы с элементарными массами m1, m2,..., mn , находящиеся на расстоянии r1, r2,..., rn от оси. 

При вращении твердого тела относительно неподвижной оси каждый из его элементарных объемов массами mi опишет окружность соответствующих радиусов ri; при этом объем будет иметь соответствующую линейную скорость vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:   (1)  Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:   или    Используя выражение (1), получаем    где Jz - момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела   (2)  Из сравнения формулы (2) с выражением для кинетической энергии поступательно движущегося тела (T=mv2/2), мы видим, что момент инерции является мерой инертности тела при вращательном движении. Формула (2) справедлива для тела вращающегося вокруг неподвижной оси.  В качеcтве примера напишем формулу для плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения. Его энергия движения складывается из энергии поступательного движения и энергии вращения:    где m - масса катящегося тела; vc - скорость центра масс тела; Jc - момент инерции тела относительно оси, проходящей через его центр масс; ω - угловая скорость тела.

Основное уравнение динамики вращательного движения

Согласно уравнению (5.8) второй закон Ньютона для вращательного движения

По определению угловое ускорение   и тогда это уравнение можно

переписать следующим образом

с учетом (5.9)

или

(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела  , равно импульсу момента  всех внешних сил, действующих на это тело.

9.

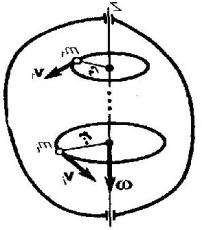
5.6. Момент импульса материальной точки и твердого тела

Векторное произведение радиуса-вектора   материальной точки на ее импульс:   называют моментом импульса  , этой точки относительно точки О (рис.5.4)

. Вектор   иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы   и   и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от   к   происходит против часовой стрелки).

Векторную сумму моментов импульсов   всех материальных точек системы называют моментом импульса (количества движения)   системы относительно точки О:

Векторы   и   взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому  . Сучетом связи линейных и угловых величин

и направлен вдоль оси вращения тела в ту же сторону, что и вектор  .

Таким образом.

Момент импульса тела относительно оси вращения

т.е.

(5.9)

Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим,момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.

Закон сохранения момента импульса есть проявление изотропности пространства.

10. О́бщая тео́рия относи́тельности (ОТО; нем. allgemeine Relativitätstheorie) — геометрическая теория тяготения, развивающая специальную теорию относительности (СТО), опубликованная Альбертом Эйнштейном в 1915—1916 годах[1][2]. В рамках общей теории относительности, как и в другихметрических теориях, постулируется, что гравитационные эффекты обусловлены не силовым взаимодействием тел и полей, находящихся впространстве-времени, а деформацией самого́ пространства-времени, которая связана, в частности, с присутствием массы-энергии. Общая теория относительности отличается от других метрических теорий тяготения использованием уравнений Эйнштейна для связи кривизны пространства-времени с присутствующей в нём материей.

Классическая теория тяготения Ньютона основана на понятии силы тяготения, которая является дальнодействующей силой: она действует мгновенно на любом расстоянии. Этот мгновенный характер действия несовместим с понятием поля в современной физике. В теории относительности никакая информация не может распространиться быстрее скорости света в вакууме.

Математически сила гравитации Ньютона выводится из потенциальной энергии тела в гравитационном поле. Потенциал гравитации, соответствующий этой потенциальной энергии, подчиняется уравнению Пуассона, которое не инвариантно при преобразованиях Лоренца. Причина неинвариантности заключается в том, что энергия в специальной теории относительности не является скалярной величиной, а переходит во временну́ю компоненту 4-вектора. Векторная же теория гравитации оказывается аналогичной теории электромагнитного поля Максвелла и приводит к отрицательной энергии гравитационных волн, что связано с характером взаимодействия: одноимённые заряды (массы) в гравитации притягиваются, а не отталкиваются, как в электромагнетизме[6]. Таким образом, теория гравитации Ньютона несовместима с фундаментальным принципом специальной теории относительности — инвариантностью законов природы в любой инерциальной системе отсчёта, а прямое векторное обобщение теории Ньютона, впервые предложенное Пуанкаре в 1905 году в его работе «О динамике электрона»[7], приводит к физически неудовлетворительным результатам.

Эйнштейн начал поиск теории гравитации, которая была бы совместима с принципом инвариантности законов природы относительно любой системы отсчёта. Результатом этого поиска явилась общая теория относительности, основанная на принципе тождественности гравитационной и инертной массы.

Преобразования Лоренца

Исходя из сформулированных выше постулатов теории относительности Эйнштейна, можно найти законы преобразований, связывающие межу собой пространственные координаты и время в двух системах отсчета, движущихся прямолинейно и равномерно относительно друг друга.

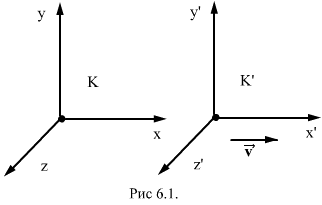
Пусть х, у, z, и х’, у’, z’ и t’,- координаты и время в инерциальных систем отсчета K и K’, а v - скорость их относительного движения (рис. 6.1).

При этом нет никаких оснований полагать, что время в системе   совпадает со временем в системе K, как это безоговорочно принималось в классической физике. Для просторы выкладок выберем направление скорости за направление осей х и  . Предположим, что в некоторый момент времени t’ в точке скоординатами  происходит некоторый физический процесс, который назовем событием. Нашей задачей является нахождение «координат» события в системе отсчета K’, т.е. нахождение величин х, y, z, t, характеризующих тот же физический процесс в системе K.

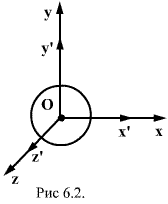
Выберем за начало отсчета времени t=0 тот момент, в который начало координат системы K’ совпадало с началом координат системы K. Пусть в момент времени t=0 из начала координат начала распространяться сферическая электромагнитная волна (рис.6.2). В системе K уравнение волновой поверхности имеет вид.

или

(6.1)

Поскольку, согласно принципу относительности Эйнштейна, закон и величина скорости распространения волны должны быть одинаковыми во всех инерциальных системах отсчета, наряду с этим уравнением с равным правом можно написать уравнение сферической волны в системе K’.

Так как в начальный момент времени начало координат систем совпадали, то

(6.2)

Формулы преобразования координат и времени должны, во-первых, не нарушать соотношений (6.1) и (6.2), а, во-вторых, быть линейными. Требования линейности связано с однородностью пространства. Т.к. движение системы K’ происходит только вдоль оси х преобразование координат у и z должно иметь вид

Закон преобразования х’ через х можно написать, исходя из следующегосоображения: если в момент времени t=0 начала систем координат K и K’ совпадали, то координата плоскости х’ в системе K запишется х=νt. Следовательно, в самом общем случае можно написать

(6.3)

где коэффициент   может зависеть лишь от скорости относительного движения. Не делая никаких произвольных допущений о совпадении времени в двух системах отсчета, мы можем представить t’ в виде линейной однородной функции х и t

(6.4)

Kоэффициенты   и   могут, вообще говоря, зависеть от скорости v. Если бы оказалось, что  , а  , то мы вернулись бы к преобразованиям Галилея. Для определения коэффициентов  ,   и  , отвечающих Требованиям принципа относительности Эйнштейна, мы должны подставить (6.3) и (6.5) в (6.2). Это дает

Для выполнения тождества необходимо приравнять коэффициенты при х2,t2и хt. Раскрыв скобки и проведя соответствующие преобразования получим:

Из этих трех уравнений находим неизвестные величины  ,   и  ,:

При этом всюду мы выбрали положительный знак корня. Подставляя значения  ,   и   в преобразования координат (6.3) и (6.4) находим:

(6.5)

Эти формулы носят название преобразований Лоренца. Формулы обратного преобразования от штрихованных к не штрихованным величинам:

(6.6)

Преобразования Лоренца приводят к выводам, коренным образом противоречащим привычным представлениям о свойствах времени и пространства, сложившимся на основе повседневного опыта. Рассмотрим несколько примеров применения преобразований Лоренца.

11. Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении икомнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.

Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна).

Закон распределения молекул идеального газа во внешнем силовом поле

При рассмотрении кинетической теории газов и закона распределения Максвелла предполагалось, что на молекулы газа не действуют никакие силы, за исключением ударов молекул. Поэтому, молекулы равномерно распределяются по всему сосуду. В действительности молекулы любого газа всегда находятся в поле тяготения Земли. Вследствие этого, каждая молекула массой m испытывает действие силы тяжести f =mg.

Выделим горизонтальный элемент объема газа высотой dh и площадью основания S (рис. 11.2). Считаем газ однородным и температуру его постоянной. Число молекул в этом объеме равно произведению его объема dV=Sdh на число молекул   в единице объема. Полный вес молекул в выделенном элементе равен

Действие веса dF вызывает давление, равное

(11.2)

минус - т.к. при увеличении dh давление уменьшается. Согласно основному уравнению молекулярно-кинетической теории

(11.3)

Приравнивая правые части (11.2) и (11.3), получаем

или

Интегрируя это выражение в пределах от   до h (соответственно концентрация изменяется от   до n):

получим

Потенцируя полученное выражение, находим

(11.4)

Показатель степени при exp имеет множитель   , который определяет приращение потенциальной энергии молекул газа. Если переместить молекулу с уровня   до уровня h, то изменение ее потенциальной энергии будет

Тогда уравнение для концентрации молекул преобразуется к виду

(11.5)

Это уравнение отображает общий закон Больцмана и дает распределение числа частиц в зависимости от их потенциальной энергии. Он применим к любой системе частиц, находящихся в силовом поле, например в электрическом.

Основное уравнение м.к.т. идеальных газов. Температура

Так принято называть выводимое из м.к.т. уравнение, определяющее давление газа. Важным здесь является выяснение молекулярно-кинетического понятия температуры. Для дальнейшего нам понадобится понятие концентрации молекул. Будем называть концентрацией n число молекул в единице объема.

(10.1)

Первая формула справедлива всегда, вторая – в случае, если концентрация всюду в объеме постоянна.

Через концентрацию можно выразить и давление газа   . Используя введенную ранее постоянную Больцмана  запишем  . Итак, получим

(10.2)

Необходимо вывести это же уравнение из молекулярно-кинетической теории, иными словами, найти давление газа на стенку. Давление – результат ударов молекул. Импульс, переданный всеми молекулами за секунду, – это и есть сила давления т.е. PS, где S – площадь стенки. Поскольку при каждом соударении молекул полный импульс сохраняется, для расчета давления не нужно учитывать соударения молекул между собой.

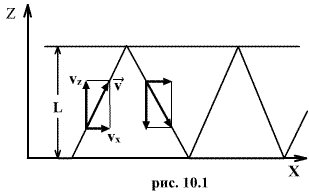
Рассмотрим молекулу (рис.10.1), движущуюся между стенками сосуда, расстояние между которыми L. При ударе о верхнюю стенку меняется только составляющая скорости   . Эта составляющая меняется на   .

Изменение импульса молекулы при ударе (т.е. передаваемый стенке импульс) равно δp=2mvz . Это изменение импульса приходится на время   , протекающее между двумя ударами о верхнюю стенку, которое равно   .

Итак, средняя сила, действующая со стороны одной молекулы на стенку, равна

У разных молекул разные скорости, поэтому вместо   надо записать   , где i – номер молекулы. Полная сила со стороны всех молекул   . Для того чтобы найти давление, нужно эту силу разделить на площадь стенки S:

Запишем теперь просуммируем по всем N молекулам

Ввиду равноправия осей x,y,z при т.д.р. три суммы справа должны быть (при большом числе молекул) равны между собой, откуда

.

Введем понятие среднеквадратичной скорости (она называется еще тепловой скоростью vi ). Для этого необходимо найти средний квадрат скорости. Он, очевидно, равен

(10.3)

Выражение (10.3) вполне аналогично выражению для средней арифметической скорости

(10.4)

только в (10.4) складываются абсолютные величины скоростей молекул, а в (10.3) – квадраты скоростей.

Среднеквадратичной, или тепловой скоростью называется корень квадратный из выражения (10.3):

(10.5)

Заметим, что   всегда больше средней арифметической скорости (10.4). Это легко проверить, подставляя вместо   любые (неравные) числа.

Возвращаясь к выводу уравнения м.к.т. газов, запишем, пользуясь уравнением (10.3):

.

Подставляя полученное выражение в выражение для P, получим

.

Наконец, учитывая, что   - концентрация, и замечая, что

есть средняя кинетическая энергия поступательного движения молекул, получим

(10.6)

Это и есть основное уравнение м.к.т. идеальных газов. Оно читается так: давление газа равно  кинетической энергии поступательного движения молекул, заключенных в единице объема.

Сравнивая (10.6) с (10.2), получим очень важное равенство

(10.7)

Это выражение объясняет молекулярно-кинетический смысл понятия температуры.

Температура – это средняя кинетическая энергия движения молекул (выраженная в других единицах).

В этом определении очень важным является слово «средняя». Если изъять из газа наиболее медленные молекулы, полная кинетическая энергия всех молекул уменьшится, но температура повысится, так как увеличится средняя энергия.

Записывая

(10.8)

найдем среднеквадратичную скорость молекул

(10.9)

Эта скорость пропорциональна корню квадратному из температуры.

Можно записать (10.9) в виде

(10.10)

Для молекулы кислорода (μ=0,032 кг/моль) при Т=300К 483 м/с. Для молекулы водорода (μ=0,002 кг/моль) при этой же температуре скорость равна vТ=1932 м/с, т. е. она больше, чем у молекулы кислорода, в 4 раза.

Весьма важным является то обстоятельство, что в условиях т. д. р., которые рассматриваются, средняя кинетическая энергия молекулы (10.8) не зависит от массы молекулы. Если мешать несколько газов, например Н2, О2 и газ с молекулами, в сотни раз более тяжелыми, чем молекулы водорода, то при условии, что смесь будет находиться в состоянии т. д. р., средняя кинетическая энергия молекул всех газов будет одинакова. Тяжелые молекулы будут двигаться с малыми скоростями, такими, чтобы их средняя кинетическая энергия как раз равнялась энергии легких молекул.

Средняя кинетическая энергия броуновых частиц в жидкости, несмотря на огромную (по сравнению с молекулами) массу этих частиц, такая же, как у молекул.

Можно рассматривать тяжелый и легкий газ как две системы, находящиеся в т. д. р. друг с другом. Термодинамическое равновесие предполагает равенство температур этих систем. Иначе тепло будет передаваться от более горячей системы к более холодной.