43) Процеси відновлення

44) Генеральною сукупністю в математичній статистиці називається множина однотипних об’єктів, кількісна чи якісна ознака яких підлягає вивченню. Підмножина об’єктів, дібраних у відповідний спосіб із генеральної сукупності, називається вибірковою сукупністю. Вважаємо, що ознака, яка вивчається, є випадковою величиною Х із функцією розподілу Результати вибірки розглядатимемо як послідовність незалежних однаково розподілених випадкових величин Закон розподілу для всіх визначається функцією Результати вибірки — реалізації випадкових величин — позначатимемо відповідно через Розмістивши ці числа в порядку зростання і записавши частоти з якими зустрічаються ці значення, дістанемо варіаційний, або статистичний, ряд:

			…
Частоти			…

На підставі такого ряду можна побудувати статистичну функцію розподілу 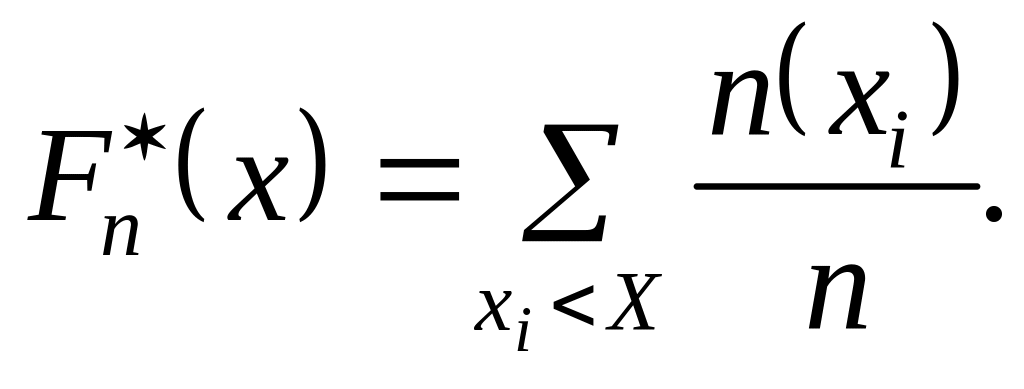Якщо , то статистична функція розподілу збігається д теоретичної функції розподілу.

45) Дискретний статистичний розподіл вибірки

Перелік варіант варіаційного ряду і відповідних їм частот, або відносних частот, називають дискретним статистичним розподілом вибірки.

У табличній формі він має такий вигляд:

Дискретний статистичний розподіл вибірки можна подати емпіричною функцією F ^(x).

Емпірична функція F ^(x) та її властивості. Функція аргументу х, що визначає відносну частоту події X < x, тобто , називається емпіричною, або комулятою.

Тут n — обсяг вибірки;

n_x — кількість варіант статистичного розподілу вибірки, значення яких менше за фіксовану варіанту х;

F ^(x) — називають ще функцією нагромадження відносних частот.

Властивості F ^(x):

1) 0  F ^(x)  1;

2) F(x_min) = 0, де x_min є найменшою варіантою варіаційного ряду;

3)  , де x_max є найбільшою варіантою варіаційного ряду;

4) F(x) є неспадною функцією аргументу х, а саме: F(x₂)  F(x₁) при x₂  x₁.

Інтервальний статистичний розподіл

h	x1 – x2	x2 – x3	x3 – x4	…	xk–1 – xk
ni	n1	n2	n3	…	Nk
Wi	W1	W2	W3	…	Wk

Перелік часткових інтервалів і відповідних їм частот, або відносних частот, називають інтервальним статистичним розподілом вибірки.

У табличній формі цей розподіл має такий вигляд:Тут h = x_i – x_i–1 є довжиною часткового i-го інтервалу. Як правило, цей інтервал береться однаковим.

Інтервальний статистичний розподіл вибірки можна подати графічно у вигляді гістограми частот або відносних частот, а також, як і для дискретного статистичного розподілу, емпіричною функцією F ^(x) (комулятою).

46) Полігон частот і відносних частот. Дискретний статистичний розподіл вибірки можна зобразити графічно у вигляді ламаної лінії, відрізки якої сполучають координати точок (x_i; n_i), або (x_i; W_i).

У першому випадку ламану лінію називають полігоном частот, у другому — полігоном відносних частот.

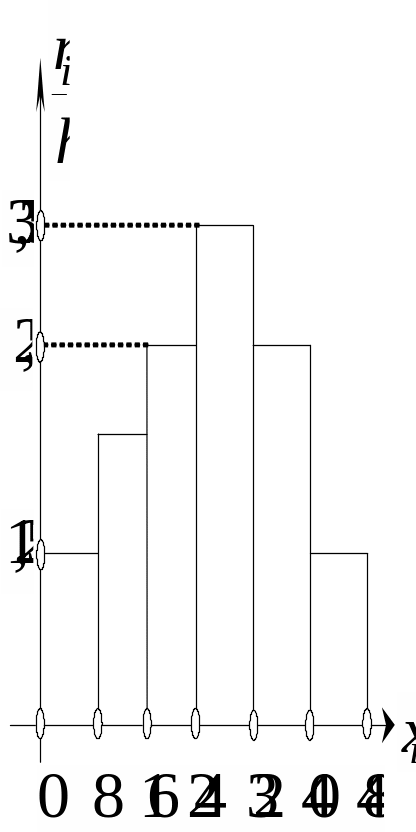
Гістограма частот та відносних частот. Гістограма частот являє собою фігуру, яка складається з прямокутників, кожний з яких має основу h і висотy .

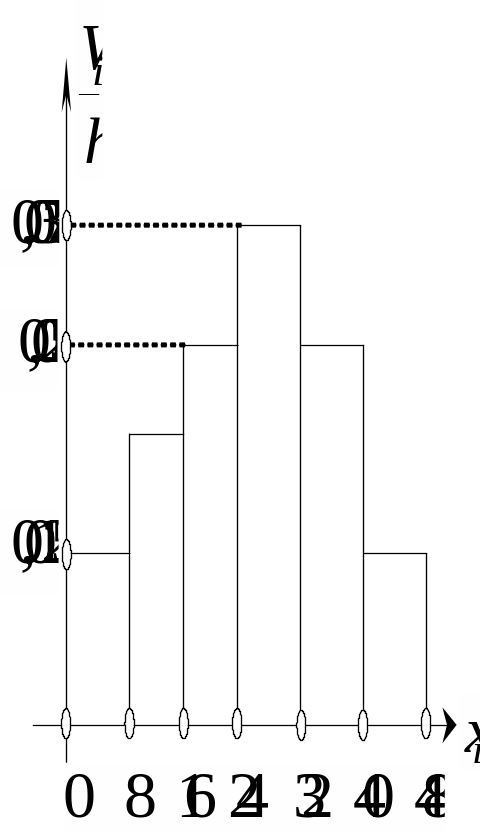
Гістограма відносних частот є фігурою, що складається з прямокутників, кожний з яких має основу завдовжки h і висоту, що дорівнює .

Площа гістограми частот

Площа гістограми відносних частот .